9.2.2总体百分位数的估计 课件(共15张PPT)
文档属性
| 名称 | 9.2.2总体百分位数的估计 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 301.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 19:43:43 | ||
图片预览



文档简介
(共15张PPT)
9.2.2 总体百分位数的估计
一、温故新知,导入新课
【回顾一】如何求一组数据的中位数?
先排序,数据个数为奇数个取中间值,偶数个取中间两个的平均数;
【回顾二】中位数一定是给定这组数据中的一个数吗?
不一定,比如给定数据个数为偶数个时,中位数就可能不在这组数据中。
【回顾三】一组数据中小于等于中位数的数据占比至少为多少?大于等于中位数的占比至少为多少?
均至少为50%
二、情景导入,生成概念
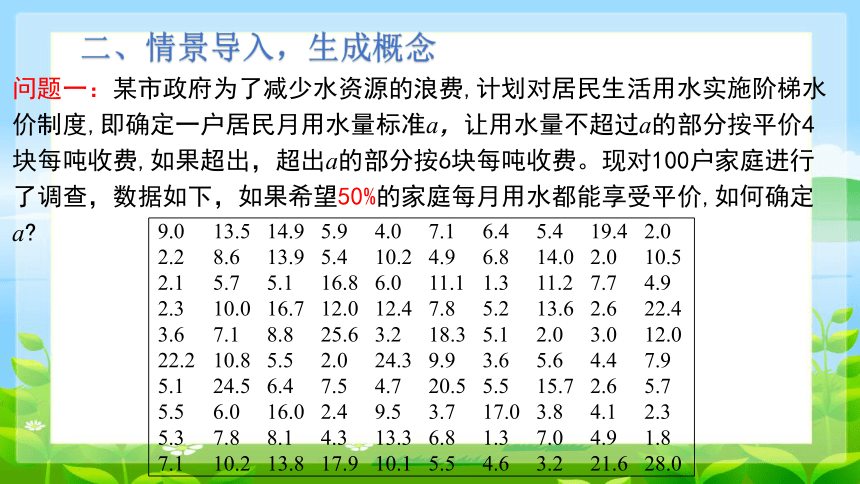
问题一:某市政府为了减少水资源的浪费,计划对居民生活用水实施阶梯水价制度,即确定一户居民月用水量标准a,让用水量不超过a的部分按平价4块每吨收费,如果超出,超出a的部分按6块每吨收费。现对100户家庭进行了调查,数据如下,如果希望50%的家庭每月用水都能享受平价,如何确定a
9.0 13.5 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.6 13.9 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6 28.0
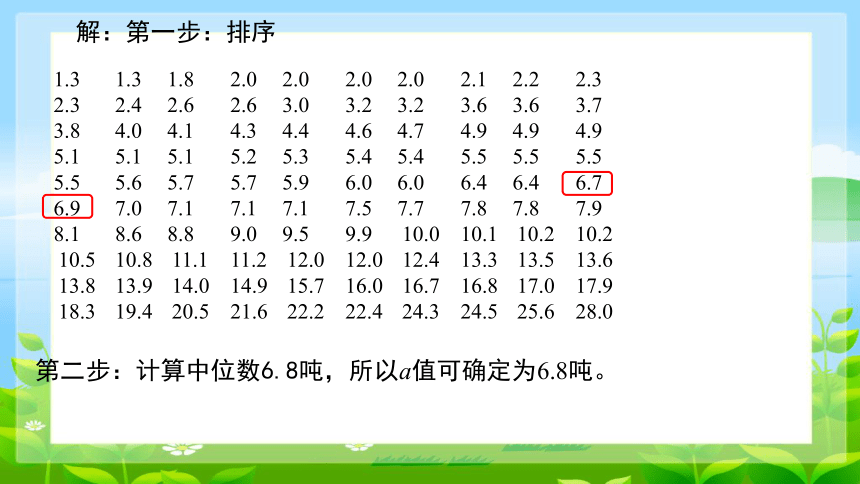
第二步:计算中位数6.8吨,所以a值可确定为6.8吨。
解:第一步:排序
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3
2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7
3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9
5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5
5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.7
6.9 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9
8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2
10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.5 13.6
13.8 13.9 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9
18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
三、新课讲授,深入探究
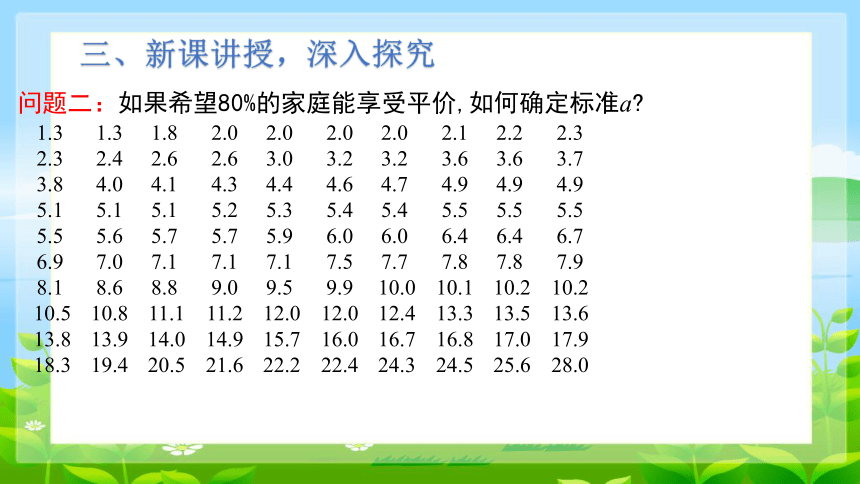
问题二:如果希望80%的家庭能享受平价,如何确定标准a
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3
2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7
3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9
5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5
5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.7
6.9 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9
8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2
10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.5 13.6
13.8 13.9 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9
18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少 数据 这个值,且至少有 的数据 这个值,也可以称作p%分位数。
第p百分位数
p%
≤
( 100-p)%
≥
三、新课讲授,深入探究
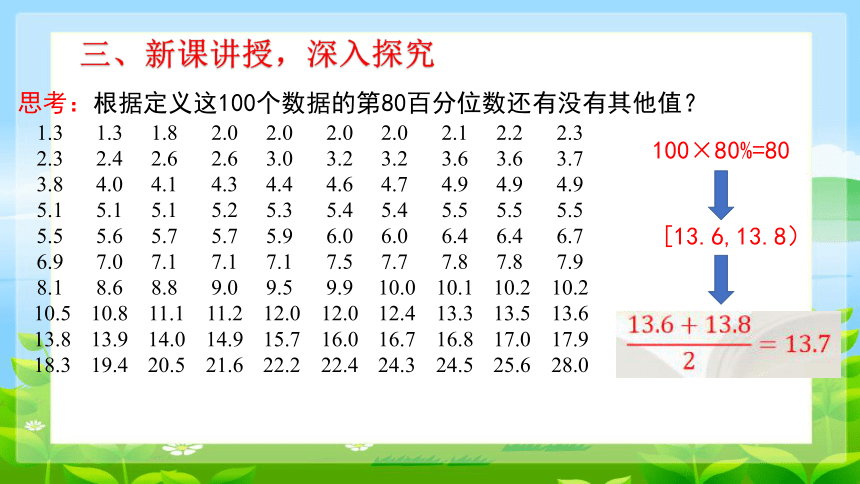
思考:根据定义这100个数据的第80百分位数还有没有其他值?
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3
2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7
3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9
5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5
5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.7
6.9 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9
8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2
10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.5 13.6
13.8 13.9 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9
18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
100×80%=80
[13.6,13.8)
问题3:由于登记员的失误,第100个数据被抹掉了,你能不能只利用这99个数据求出80%的家庭能享受平价的标准的a值?
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3
2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7
3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9
5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5
5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.7
6.9 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9
8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2
10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.5 13.6
13.8 13.9 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9
18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
三、新课讲授,深入探究
99×80%=79.2
例. 以下数据为参加数学竞赛决赛的15人的成绩:73,72,84,88,92,93,95,55,83,90,79,73,82,90,69,
(1)试求这15人成绩的第25百分位数;(2)求这15人成绩的第60百分位数。
四、概念辨析,明确方法
解:(1)第一步:排序:55,69,72,73,73,79,82,83,84,88,90,90,92,93,95;
第二步:15×25%=3.75;
第三步:第4位同学的成绩,即73可以作为第25百分位数。
(2)第一步:排序:55,69,72,73,73,79,82,83,84,88,90,90,92,93,95;
第二步:15×60%=9;
第三步:取第9位和第10位同学的平均成绩,即86分为这组数据第60百分位数。
四、概念辨析,明确方法
思考1:结合第p百分位数定义和这两道题目,如果要求一组数据的第p百分位数,可以分为几类?
思考2:试总结求一组数据第p百分位数的方法和步骤。
几个重要的百分位数
常用分位数:第25百分位数,第50百分位数,第75百分位数.
这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数.
像第1百分位数,第5百分位数,第95百分位数,第99百分位数也常用.
25%
第一四分位数
(下四分位数)
50%
75%
中位数
第三四分位数
(上四分位数)
五、课堂小结
1.本节课你学到了什么?
2.请你用自己的语言总结描述第p百分位数在一组数据中的地位。
2.数据7, 8.4, 8.4, 8.4, 8.6, 8.7, 9, 9.1的30%分位数为
A.8.4 B.8.5 C.8.6 D.8.3
√
3.以下数据为参加数学竞赛决赛的15人的成绩(单位:分):78, 70,72,86,88,79,80,81,94,84,56,98,83,90,91,则这15人成绩的第80百分位数是
A.90 B.90.5 C.91 D.91.5
√
1.思考辨析(正确的画“√”,错误的画“×”)
(1)若一组样本数据各不相等,则其75%分位数大于25%分位数. ( )
(2)若一组样本数据的10%分位数是23,则在这组数据中有10%的数据大于23.( )
(3)若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24.( )
√
√
×
六、目标检测,课堂反馈
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的第50百分位数吗?
七、思考拓展
9.2.2 总体百分位数的估计
一、温故新知,导入新课
【回顾一】如何求一组数据的中位数?
先排序,数据个数为奇数个取中间值,偶数个取中间两个的平均数;
【回顾二】中位数一定是给定这组数据中的一个数吗?
不一定,比如给定数据个数为偶数个时,中位数就可能不在这组数据中。
【回顾三】一组数据中小于等于中位数的数据占比至少为多少?大于等于中位数的占比至少为多少?
均至少为50%
二、情景导入,生成概念
问题一:某市政府为了减少水资源的浪费,计划对居民生活用水实施阶梯水价制度,即确定一户居民月用水量标准a,让用水量不超过a的部分按平价4块每吨收费,如果超出,超出a的部分按6块每吨收费。现对100户家庭进行了调查,数据如下,如果希望50%的家庭每月用水都能享受平价,如何确定a
9.0 13.5 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.6 13.9 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6 28.0
第二步:计算中位数6.8吨,所以a值可确定为6.8吨。
解:第一步:排序
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3
2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7
3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9
5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5
5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.7
6.9 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9
8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2
10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.5 13.6
13.8 13.9 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9
18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
三、新课讲授,深入探究
问题二:如果希望80%的家庭能享受平价,如何确定标准a
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3
2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7
3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9
5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5
5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.7
6.9 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9
8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2
10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.5 13.6
13.8 13.9 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9
18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少 数据 这个值,且至少有 的数据 这个值,也可以称作p%分位数。
第p百分位数
p%
≤
( 100-p)%
≥
三、新课讲授,深入探究
思考:根据定义这100个数据的第80百分位数还有没有其他值?
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3
2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7
3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9
5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5
5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.7
6.9 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9
8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2
10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.5 13.6
13.8 13.9 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9
18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
100×80%=80
[13.6,13.8)
问题3:由于登记员的失误,第100个数据被抹掉了,你能不能只利用这99个数据求出80%的家庭能享受平价的标准的a值?
1.3 1.3 1.8 2.0 2.0 2.0 2.0 2.1 2.2 2.3
2.3 2.4 2.6 2.6 3.0 3.2 3.2 3.6 3.6 3.7
3.8 4.0 4.1 4.3 4.4 4.6 4.7 4.9 4.9 4.9
5.1 5.1 5.1 5.2 5.3 5.4 5.4 5.5 5.5 5.5
5.5 5.6 5.7 5.7 5.9 6.0 6.0 6.4 6.4 6.7
6.9 7.0 7.1 7.1 7.1 7.5 7.7 7.8 7.8 7.9
8.1 8.6 8.8 9.0 9.5 9.9 10.0 10.1 10.2 10.2
10.5 10.8 11.1 11.2 12.0 12.0 12.4 13.3 13.5 13.6
13.8 13.9 14.0 14.9 15.7 16.0 16.7 16.8 17.0 17.9
18.3 19.4 20.5 21.6 22.2 22.4 24.3 24.5 25.6 28.0
三、新课讲授,深入探究
99×80%=79.2
例. 以下数据为参加数学竞赛决赛的15人的成绩:73,72,84,88,92,93,95,55,83,90,79,73,82,90,69,
(1)试求这15人成绩的第25百分位数;(2)求这15人成绩的第60百分位数。
四、概念辨析,明确方法
解:(1)第一步:排序:55,69,72,73,73,79,82,83,84,88,90,90,92,93,95;
第二步:15×25%=3.75;
第三步:第4位同学的成绩,即73可以作为第25百分位数。
(2)第一步:排序:55,69,72,73,73,79,82,83,84,88,90,90,92,93,95;
第二步:15×60%=9;
第三步:取第9位和第10位同学的平均成绩,即86分为这组数据第60百分位数。
四、概念辨析,明确方法
思考1:结合第p百分位数定义和这两道题目,如果要求一组数据的第p百分位数,可以分为几类?
思考2:试总结求一组数据第p百分位数的方法和步骤。
几个重要的百分位数
常用分位数:第25百分位数,第50百分位数,第75百分位数.
这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数.
像第1百分位数,第5百分位数,第95百分位数,第99百分位数也常用.
25%
第一四分位数
(下四分位数)
50%
75%
中位数
第三四分位数
(上四分位数)
五、课堂小结
1.本节课你学到了什么?
2.请你用自己的语言总结描述第p百分位数在一组数据中的地位。
2.数据7, 8.4, 8.4, 8.4, 8.6, 8.7, 9, 9.1的30%分位数为
A.8.4 B.8.5 C.8.6 D.8.3
√
3.以下数据为参加数学竞赛决赛的15人的成绩(单位:分):78, 70,72,86,88,79,80,81,94,84,56,98,83,90,91,则这15人成绩的第80百分位数是
A.90 B.90.5 C.91 D.91.5
√
1.思考辨析(正确的画“√”,错误的画“×”)
(1)若一组样本数据各不相等,则其75%分位数大于25%分位数. ( )
(2)若一组样本数据的10%分位数是23,则在这组数据中有10%的数据大于23.( )
(3)若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24.( )
√
√
×
六、目标检测,课堂反馈
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的第50百分位数吗?
七、思考拓展
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
