7.1.2 一元线性回归方程 课件(共18张PPT)
文档属性
| 名称 | 7.1.2 一元线性回归方程 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 428.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 23:28:37 | ||
图片预览






文档简介
(共18张PPT)
7.1.2 一元线性回归方程
1.会求一元线性回归方程并能根据线性回归方程进行预测.
对于给定的两个变量X和Y(如身高和体重),
假设有n对观测值(x1,y1),(x2,y2),(x3,y3),...,(xn,yn),拟合的直线是Y=a+bX,
样本点与这条直线的距离为
希望a,b的取值能使上式达到最小.这个方法称为最小二乘法.
先研究简单的情形,考虑3对数据(x1,y1),(x2,y2),(x3,y3),
下面用向量的方法解决这个问题.
即:求a,b的值,使得偏差yi-(a+bxi)(i=1,2,3)的平方和最小,
[y1-(a+bx1)]2+[y2-(a+bx2)]2+[y3-(a+bx3)]2达到最小.
用向量的语言描述问题.
“求a,b的值,使得偏差yi-(a+bxi)(i=1,2,3)的平方和最小”
等价于
“求a,b的值,使得向量 (y1-(a+bx1),y2-(a+bx2),y3-(a+bx3))的长度最小”
(y1-(a+bx1) , y2-(a+bx2) , y3-(a+bx3))
=(y1 , y2 , y3)-(a+bx1 , a+bx2 , a+bx3)
=(y1 , y2 , y3)-[(a , a , a)+(bx1 , bx2 , bx3)]
=(y1 , y2 , y3)-[a(1 , 1 , 1)+b(x1 , x2 , x3)]
其中, 均为已知向量.
问题转化为:求a,b的值,使 的长度最小.
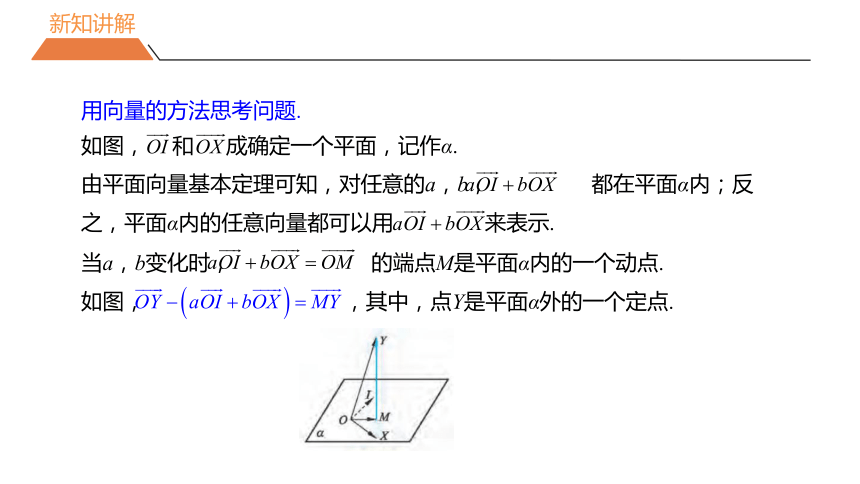
用向量的方法思考问题.
如图, 和 成确定一个平面,记作α.
由平面向量基本定理可知,对任意的a,b, 都在平面α内;反之,平面α内的任意向量都可以用 来表示.
当a,b变化时, 的端点M是平面α内的一个动点.
如图, ,其中,点Y是平面α外的一个定点.
要使 最小,即 最小,由点到平面距离的定义,
当 ⊥α时,线段MY的长度最短,
即 与平面α垂直时, 的长度最小.
根据线面垂直的判定定理,要使 与平面α垂直,只需其与平面α内的两个不共线的向量 和 均垂直.
用向量的方法解决问题.
求 最小时的a,b的值,就是求 与 和 的数量积分别为0时的a,b的值,即
用向量的坐标表示,即
记
化简,得
则
如果把它的解记作 得到:
①
②
①,②两式推广到n对数据(x1,y1),(x2,y2),...,(xn,yn)仍然成立,即:使
达到最小的a,b取值为
其中,
概念讲解
直线方程 称作Y关于X的线性回归方程,相应的直线称作Y关于X的回归直线(如图), 是这个线性回归方程的系数.
根据表中身高、体重的数据,利用上述方法得到身高和体重满足的线性回归方程为Y=0.648X-55.139.
编号 1 2 3 4 5 6 7 8 9
身高/cm 165 157 155 175 168 157 178 160 163
体重/kg 52 44 45 55 54 47 62 50 53
由此可知,一个身高166cm的15岁男生,他的体重大致为52.429kg.
同理,一个身高175cm的15岁男生,他的体重大致为58.261kg.
注意:身高和体重之间并没有函数关系,得到的线性回归方程只是对其变化趋势的一种近似描述.对一个给定身高的人,人们可以用这个方程来估计这个人的体重.
例1:如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
(1)求出y关于x的回归直线方程;
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
解:(1)将每个x的值都减去80可得-4,2,-8,7,13,-2,9,-14,1,-4.
这些数字的平均数为0,因此=80.
将每个y的值都减去80可得0,7,-5,6,20,-1,13,-12,5,-3.
这些数字的平均数为3,因此=83.
因此
回归直线方程为
例1:如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
(1)求出y关于x的回归直线方程;
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
例1:如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
(2)该同学的数学成绩每提高3分,物理成绩估计能提高多少分?
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
(2)由回归系数 可知,x每增大1个单位时, 增大1.1个单位.
因此,数学成绩每提高3分,物理成绩估计能提高的分值为
1.1×3=3.3.
(1)画出散点图.从直观上分析数据间是否存在线性相关关系.
(2)计算 等相关数据.
(3)代入公式求出 中参数 的值.
(4)写出回归方程并对实际问题作出估计.
求线性回归方程的步骤:
归纳总结
1.为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了5次试验,得到5组数据:(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),由最小二乘法求得线性回归方程为=0.67x+54.9.若已知x1+x2+x3+x4+x5=150,则y1+y2+y3+y4+y5=( )
A.75 B.155.4
C.375 D.466.2
C
2.正常情况下,年龄在18岁到38岁的人,体重y(kg)对身高x(cm)的回归方程为
0.72x-58.2,张红同学(20岁)身高为178 cm,她的体重应该在________kg左右.
3.对具有线性相关关系的变量x和Y,测得一组数据如下表:
若已求得它们的回归直线方程的斜率为6.5,则这条回归直线方程
为 .
69.96
x 2 4 5 6 8
Y 30 40 60 50 70
根据本节课所学,回答下列问题:
1.用什么方法求回归直线方程中,,公式是什么?
2.求回归直线方程的步骤是什么?
7.1.2 一元线性回归方程
1.会求一元线性回归方程并能根据线性回归方程进行预测.
对于给定的两个变量X和Y(如身高和体重),
假设有n对观测值(x1,y1),(x2,y2),(x3,y3),...,(xn,yn),拟合的直线是Y=a+bX,
样本点与这条直线的距离为
希望a,b的取值能使上式达到最小.这个方法称为最小二乘法.
先研究简单的情形,考虑3对数据(x1,y1),(x2,y2),(x3,y3),
下面用向量的方法解决这个问题.
即:求a,b的值,使得偏差yi-(a+bxi)(i=1,2,3)的平方和最小,
[y1-(a+bx1)]2+[y2-(a+bx2)]2+[y3-(a+bx3)]2达到最小.
用向量的语言描述问题.
“求a,b的值,使得偏差yi-(a+bxi)(i=1,2,3)的平方和最小”
等价于
“求a,b的值,使得向量 (y1-(a+bx1),y2-(a+bx2),y3-(a+bx3))的长度最小”
(y1-(a+bx1) , y2-(a+bx2) , y3-(a+bx3))
=(y1 , y2 , y3)-(a+bx1 , a+bx2 , a+bx3)
=(y1 , y2 , y3)-[(a , a , a)+(bx1 , bx2 , bx3)]
=(y1 , y2 , y3)-[a(1 , 1 , 1)+b(x1 , x2 , x3)]
其中, 均为已知向量.
问题转化为:求a,b的值,使 的长度最小.
用向量的方法思考问题.
如图, 和 成确定一个平面,记作α.
由平面向量基本定理可知,对任意的a,b, 都在平面α内;反之,平面α内的任意向量都可以用 来表示.
当a,b变化时, 的端点M是平面α内的一个动点.
如图, ,其中,点Y是平面α外的一个定点.
要使 最小,即 最小,由点到平面距离的定义,
当 ⊥α时,线段MY的长度最短,
即 与平面α垂直时, 的长度最小.
根据线面垂直的判定定理,要使 与平面α垂直,只需其与平面α内的两个不共线的向量 和 均垂直.
用向量的方法解决问题.
求 最小时的a,b的值,就是求 与 和 的数量积分别为0时的a,b的值,即
用向量的坐标表示,即
记
化简,得
则
如果把它的解记作 得到:
①
②
①,②两式推广到n对数据(x1,y1),(x2,y2),...,(xn,yn)仍然成立,即:使
达到最小的a,b取值为
其中,
概念讲解
直线方程 称作Y关于X的线性回归方程,相应的直线称作Y关于X的回归直线(如图), 是这个线性回归方程的系数.
根据表中身高、体重的数据,利用上述方法得到身高和体重满足的线性回归方程为Y=0.648X-55.139.
编号 1 2 3 4 5 6 7 8 9
身高/cm 165 157 155 175 168 157 178 160 163
体重/kg 52 44 45 55 54 47 62 50 53
由此可知,一个身高166cm的15岁男生,他的体重大致为52.429kg.
同理,一个身高175cm的15岁男生,他的体重大致为58.261kg.
注意:身高和体重之间并没有函数关系,得到的线性回归方程只是对其变化趋势的一种近似描述.对一个给定身高的人,人们可以用这个方程来估计这个人的体重.
例1:如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
(1)求出y关于x的回归直线方程;
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
解:(1)将每个x的值都减去80可得-4,2,-8,7,13,-2,9,-14,1,-4.
这些数字的平均数为0,因此=80.
将每个y的值都减去80可得0,7,-5,6,20,-1,13,-12,5,-3.
这些数字的平均数为3,因此=83.
因此
回归直线方程为
例1:如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
(1)求出y关于x的回归直线方程;
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
例1:如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
(2)该同学的数学成绩每提高3分,物理成绩估计能提高多少分?
数学成绩x 76 82 72 87 93 78 89 66 81 76
物理成绩y 80 87 75 86 100 79 93 68 85 77
(2)由回归系数 可知,x每增大1个单位时, 增大1.1个单位.
因此,数学成绩每提高3分,物理成绩估计能提高的分值为
1.1×3=3.3.
(1)画出散点图.从直观上分析数据间是否存在线性相关关系.
(2)计算 等相关数据.
(3)代入公式求出 中参数 的值.
(4)写出回归方程并对实际问题作出估计.
求线性回归方程的步骤:
归纳总结
1.为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了5次试验,得到5组数据:(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),由最小二乘法求得线性回归方程为=0.67x+54.9.若已知x1+x2+x3+x4+x5=150,则y1+y2+y3+y4+y5=( )
A.75 B.155.4
C.375 D.466.2
C
2.正常情况下,年龄在18岁到38岁的人,体重y(kg)对身高x(cm)的回归方程为
0.72x-58.2,张红同学(20岁)身高为178 cm,她的体重应该在________kg左右.
3.对具有线性相关关系的变量x和Y,测得一组数据如下表:
若已求得它们的回归直线方程的斜率为6.5,则这条回归直线方程
为 .
69.96
x 2 4 5 6 8
Y 30 40 60 50 70
根据本节课所学,回答下列问题:
1.用什么方法求回归直线方程中,,公式是什么?
2.求回归直线方程的步骤是什么?
同课章节目录
