7.3.3 独立性检验的应用 课件(共12张PPT)
文档属性
| 名称 | 7.3.3 独立性检验的应用 课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 265.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-25 23:30:55 | ||
图片预览



文档简介
(共12张PPT)
7.3.3 独立性检验的应用
1.会利用独立性检验判断两个变量是否有关联.
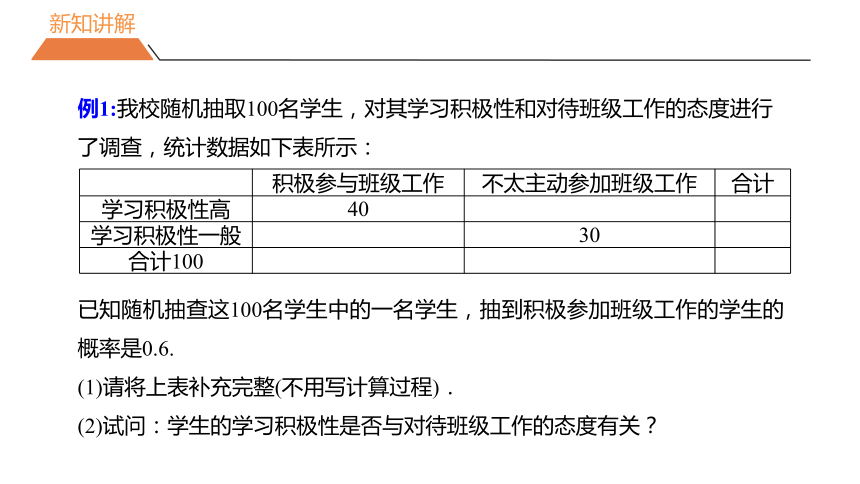
例1:我校随机抽取100名学生,对其学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参与班级工作 不太主动参加班级工作 合计
学习积极性高 40
学习积极性一般 30
合计100
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6.
(1)请将上表补充完整(不用写计算过程).
(2)试问:学生的学习积极性是否与对待班级工作的态度有关?
解:(1)由题意,积极参加班级工作人数为100×0.6=60,列联表如下:
积极参与班级工作 不太主动参加班级工作 合计
学习积极性高 40 10 50
学习积极性一般 20 30 50
合计 60 40 100
(2)由公式计算得χ2=≈16.667>6.635,
所以有99%的把握认为学习积极性与对待班级工作态度有关.
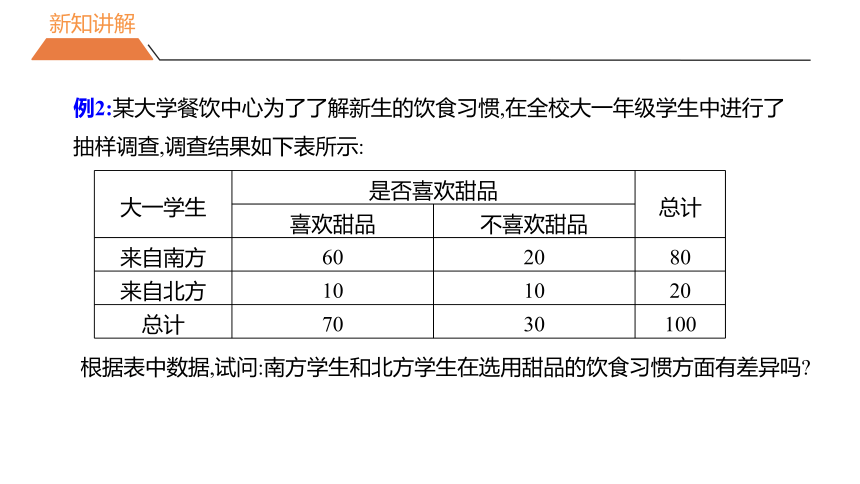
例2:某大学餐饮中心为了了解新生的饮食习惯,在全校大一年级学生中进行了抽样调查,调查结果如下表所示:
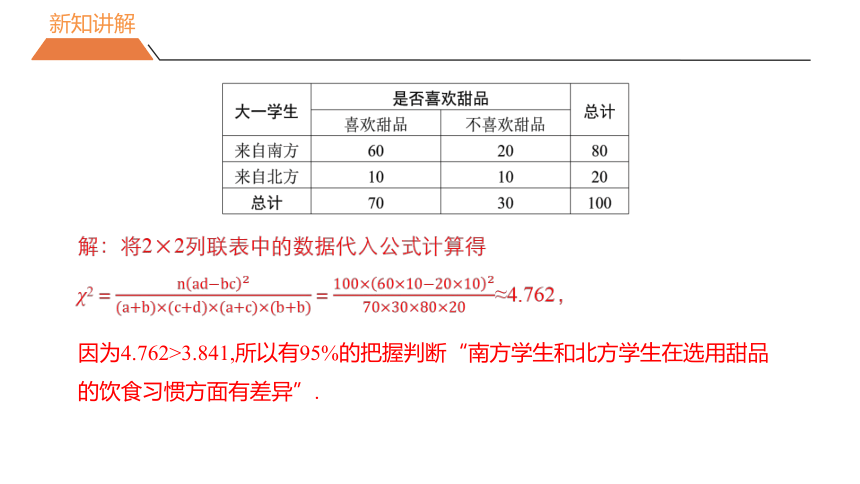
大一学生 是否喜欢甜品 总计
喜欢甜品 不喜欢甜品 来自南方 60 20 80
来自北方 10 10 20
总计 70 30 100
根据表中数据,试问:南方学生和北方学生在选用甜品的饮食习惯方面有差异吗
因为4.762>3.841,所以有95%的把握判断“南方学生和北方学生在选用甜品的饮食习惯方面有差异”.
解:将2×2列联表中的数据代入公式计算得
χ2==≈4.762,
归纳总结
用独立性检验求解实际问题的基本步骤
(1)认真读题,根据相关数据列出2×2列联表;
(2)计算:将2×2列联表中的数据代入公式求出χ2的值.
(3)判断:根据统计中的数据判断,得出结论.
例3:有甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计后,得到如下的列联表:
试问能有多大把握认为“成绩与班级有关系”
错解:由公式得:
所以有99%的把握判断成绩与班级有关系.
以上解答过程中都有哪些错误 出错的原因是什么 你如何改正 你如何防范
提示:由于对2×2列联表中a,b,c,d的位置不清楚,在代入公式时代错了数值导致计算结果错误.
正解:由公式得: χ2=≈0.653<2.706,
∴没有充分的证据判断成绩与班级有关,可以认为成绩与班级没有关系.
1.如果有95%的把握判断事件A与B有关系,那么具体计算出的数据( )
A.χ2>3.841 B.χ2<3.841 C.χ2>6.635 D.χ2<6.635
2.假设有两个分类变量X与Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表如下:则当m取下面何值时,X与Y的关系最弱( )
A.8 B.9 C.14 D.19
A
C
X Y y1 y2
x1 10 18
x2 m 26
3.某高校《统计初步》课程的教师随机调查了选该课的一些学生的情况,具体数据如下表:
95%
非统计专业 统计专业
男 13 10
女 7 20
则有_______的把握判定主修统计专业与性别有关.
针对本节课所学内容,说说你都学到了哪些知识?
独立性检验的应用
判断两个变量是否有关联
7.3.3 独立性检验的应用
1.会利用独立性检验判断两个变量是否有关联.
例1:我校随机抽取100名学生,对其学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参与班级工作 不太主动参加班级工作 合计
学习积极性高 40
学习积极性一般 30
合计100
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6.
(1)请将上表补充完整(不用写计算过程).
(2)试问:学生的学习积极性是否与对待班级工作的态度有关?
解:(1)由题意,积极参加班级工作人数为100×0.6=60,列联表如下:
积极参与班级工作 不太主动参加班级工作 合计
学习积极性高 40 10 50
学习积极性一般 20 30 50
合计 60 40 100
(2)由公式计算得χ2=≈16.667>6.635,
所以有99%的把握认为学习积极性与对待班级工作态度有关.
例2:某大学餐饮中心为了了解新生的饮食习惯,在全校大一年级学生中进行了抽样调查,调查结果如下表所示:
大一学生 是否喜欢甜品 总计
喜欢甜品 不喜欢甜品 来自南方 60 20 80
来自北方 10 10 20
总计 70 30 100
根据表中数据,试问:南方学生和北方学生在选用甜品的饮食习惯方面有差异吗
因为4.762>3.841,所以有95%的把握判断“南方学生和北方学生在选用甜品的饮食习惯方面有差异”.
解:将2×2列联表中的数据代入公式计算得
χ2==≈4.762,
归纳总结
用独立性检验求解实际问题的基本步骤
(1)认真读题,根据相关数据列出2×2列联表;
(2)计算:将2×2列联表中的数据代入公式求出χ2的值.
(3)判断:根据统计中的数据判断,得出结论.
例3:有甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计后,得到如下的列联表:
试问能有多大把握认为“成绩与班级有关系”
错解:由公式得:
所以有99%的把握判断成绩与班级有关系.
以上解答过程中都有哪些错误 出错的原因是什么 你如何改正 你如何防范
提示:由于对2×2列联表中a,b,c,d的位置不清楚,在代入公式时代错了数值导致计算结果错误.
正解:由公式得: χ2=≈0.653<2.706,
∴没有充分的证据判断成绩与班级有关,可以认为成绩与班级没有关系.
1.如果有95%的把握判断事件A与B有关系,那么具体计算出的数据( )
A.χ2>3.841 B.χ2<3.841 C.χ2>6.635 D.χ2<6.635
2.假设有两个分类变量X与Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表如下:则当m取下面何值时,X与Y的关系最弱( )
A.8 B.9 C.14 D.19
A
C
X Y y1 y2
x1 10 18
x2 m 26
3.某高校《统计初步》课程的教师随机调查了选该课的一些学生的情况,具体数据如下表:
95%
非统计专业 统计专业
男 13 10
女 7 20
则有_______的把握判定主修统计专业与性别有关.
针对本节课所学内容,说说你都学到了哪些知识?
独立性检验的应用
判断两个变量是否有关联
同课章节目录
