2016区优秀中考数学复习专题(陈圣军)有“迹”可寻求最值课件(9张)
文档属性
| 名称 | 2016区优秀中考数学复习专题(陈圣军)有“迹”可寻求最值课件(9张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-25 08:26:55 | ||
图片预览


文档简介
课件9张PPT。有“迹”可寻求最值——以《考试说明》为例探索动点最值问题求法镇海区澥浦中学 陈圣军一、直线型例1(《考试说明》43页第12题.)解析:连接OM,ON
∵MN是圆O的切线
∴ OM⊥ON
∴
∵ON=1
∴当OM最短时,MN有最小值
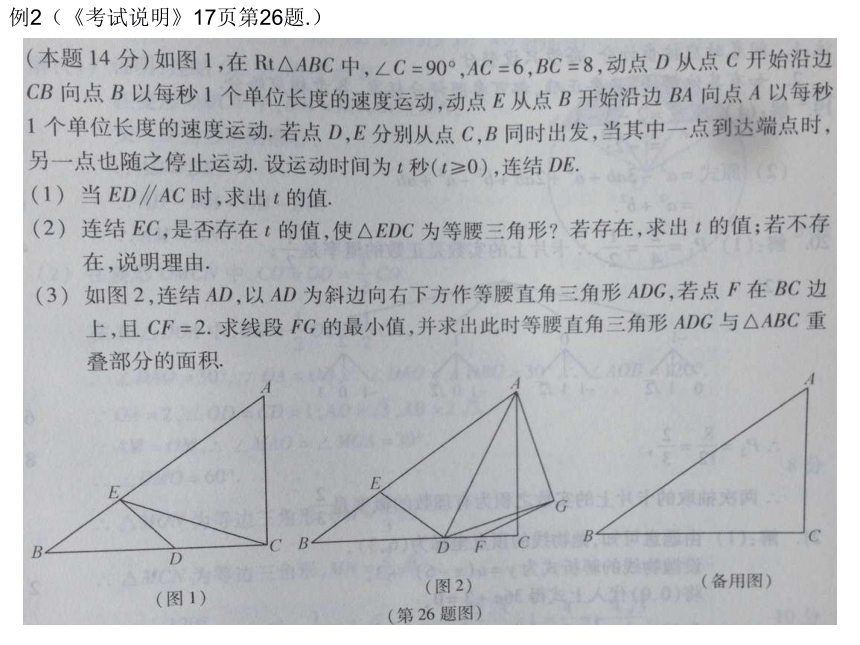
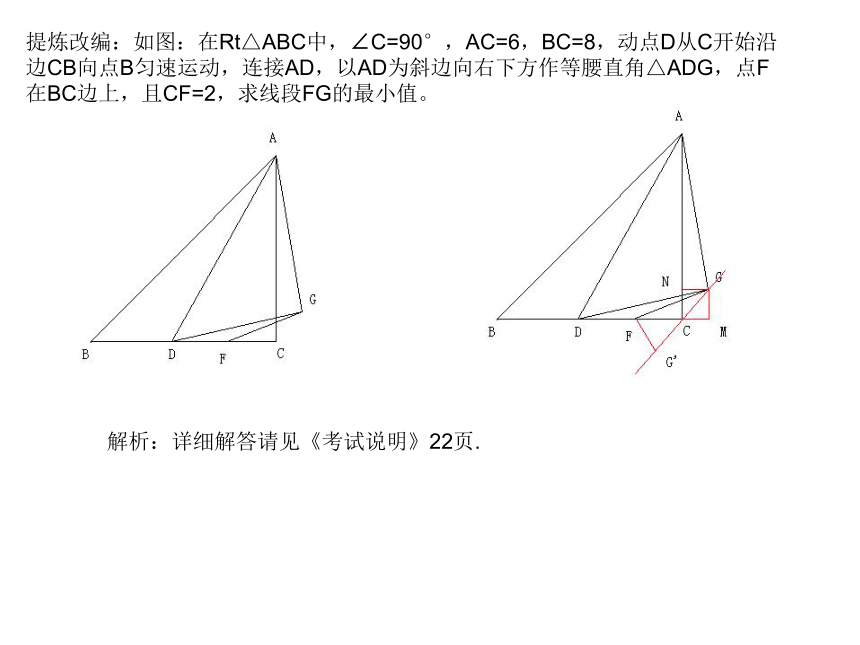
∴例2(《考试说明》17页第26题.)提炼改编:如图:在Rt△ABC中,∠C=90°,AC=6,BC=8,动点D从C开始沿
边CB向点B匀速运动,连接AD,以AD为斜边向右下方作等腰直角△ADG,点F
在BC边上,且CF=2,求线段FG的最小值。解析:详细解答请见《考试说明》22页.二、圆弧形例3(《考试说明》31页第17题.)解析:点P在以AB为直径的圆上,所以问题转化为:求圆外一点C与圆上各点连线
之长的最大值、最小值问题,易知:例4(《考试说明》49页第12题.)解析:易知点C在圆O’上,所以问题转化为:求圆O’外一点O到圆上最短距离问题,
经计算:例5(《考试说明》37页第12题.)三、其它解析:在点A运动过程中,AB长不变, ∠AOD=30°不变,考虑到同弧所对的
圆周角不变,所以构造半径为3且过AB两点的圆O’,易知OO’=3,CO‘= ,
当O,O’,C三点共线时,得最值。例6(《考试说明》31页第12题.)解析:作点A关于点O的对称点A’,连接A’B,OM四、2016中考预测7:此题由澥浦中学卓秋紫老师原创,参加2016年镇海区教师命题比赛(试卷第18题)。
∵MN是圆O的切线
∴ OM⊥ON
∴
∵ON=1
∴当OM最短时,MN有最小值
∴例2(《考试说明》17页第26题.)提炼改编:如图:在Rt△ABC中,∠C=90°,AC=6,BC=8,动点D从C开始沿
边CB向点B匀速运动,连接AD,以AD为斜边向右下方作等腰直角△ADG,点F
在BC边上,且CF=2,求线段FG的最小值。解析:详细解答请见《考试说明》22页.二、圆弧形例3(《考试说明》31页第17题.)解析:点P在以AB为直径的圆上,所以问题转化为:求圆外一点C与圆上各点连线
之长的最大值、最小值问题,易知:例4(《考试说明》49页第12题.)解析:易知点C在圆O’上,所以问题转化为:求圆O’外一点O到圆上最短距离问题,
经计算:例5(《考试说明》37页第12题.)三、其它解析:在点A运动过程中,AB长不变, ∠AOD=30°不变,考虑到同弧所对的
圆周角不变,所以构造半径为3且过AB两点的圆O’,易知OO’=3,CO‘= ,
当O,O’,C三点共线时,得最值。例6(《考试说明》31页第12题.)解析:作点A关于点O的对称点A’,连接A’B,OM四、2016中考预测7:此题由澥浦中学卓秋紫老师原创,参加2016年镇海区教师命题比赛(试卷第18题)。
同课章节目录
