2016年区优秀中考数学复习专题:新定义题专题复习课件
文档属性
| 名称 | 2016年区优秀中考数学复习专题:新定义题专题复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 622.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-25 10:09:18 | ||
图片预览








文档简介
课件28张PPT。新定义题专题复习立人中学 傅红燕 宁波市第25题频繁地出现以能力立意为目标、以增大思维容量为特色、以定义新概念为背景的自创新题型,其设计新颖,构思独特,集应用性、探索性和开放性于一体,全方面、多角度考查学生分析问题、解决问题和培养创新能力的一类综合题。考情分析一、自定义题考什么?(2015年浙江宁波第25题 12分) 如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足,我们就把∠APB叫做∠MON的智慧角.(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°. 求证:∠APB是∠MON的智慧角;(2)如图1,已知∠MON=(0°<<90°),OP=2,若∠APB是∠MON的智慧角,连结AB,用含的式子分别表示∠APB的度数和△AOB的面积;(3)如图3,C是函数图象上的一个动点,过点C的直线CD分别交轴和轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.(2014年浙江宁波第25题 12分) 课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.我们有多少种剪法,图1是其中的一种方法:定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值;(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长.(2013年浙江宁波第25题 12分) 若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.
(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
ABCD沿BE折叠(点E在AD上),使点A落(2011年浙江宁波第25题 12分)阅读下面的情景对话,然后解答问题
[来源:Zxxk.Com]
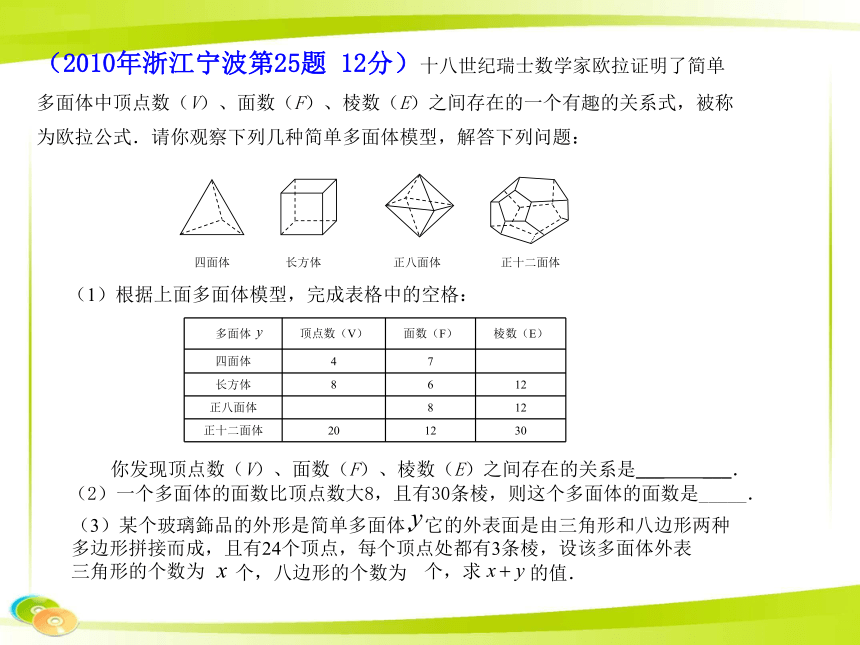
若Rt△ABC是奇异三角形,求(2010年浙江宁波第25题 12分)十八世纪瑞士数学家欧拉证明了简单
多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称
为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:(2009年浙江宁波第25题 12分) 2009年4月7日,国务院公布了
《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府
决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了
1250万元.投入资金的服务对象包括“需方”(患者等)和“供方
(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年
提高30%,投入“供方”的资金将比2008年提高20%.
(1)该市政府2008年投入改善医疗卫生服务的资金是多少万元?
(2)该市政府2009年投入“需方”和“供方”的资金各多少万元?
(3)该市政府预计2011年将有7260万元投入改善医疗卫生服务,若
从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年
的年增长率.二、自定义题怎么考?新知识型题 新知识型题是指材料中给出了新的运算法则或某一数学公式的推导与示例应用,要求学生类比应用该公式或法则解决相关问题的一类试题.材料中的法则或公式有的直接给出,也有的通过问题归纳得出,它们一般是现阶段学生未学到的知识或方法,其目的是考查学生的理解、归纳、类比迁移、主动获取新知识的能力.解答此类题目的关键是阅读题目中介绍的新知识(包括定义、公式、方法、解题思路等),然后运用这些知识去解决新问题. 定义新概念解题关键是理解新定义,再结合已学知识解答.定义新法则定义新图形14.(2015·淄博)如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,求这个“果圆”被y轴截得的弦CD的长.正确理解新定义的图形,寻找形与数的对应关系.
(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
ABCD沿BE折叠(点E在AD上),使点A落(2011年浙江宁波第25题 12分)阅读下面的情景对话,然后解答问题
[来源:Zxxk.Com]
若Rt△ABC是奇异三角形,求(2010年浙江宁波第25题 12分)十八世纪瑞士数学家欧拉证明了简单
多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称
为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:(2009年浙江宁波第25题 12分) 2009年4月7日,国务院公布了
《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府
决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了
1250万元.投入资金的服务对象包括“需方”(患者等)和“供方
(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年
提高30%,投入“供方”的资金将比2008年提高20%.
(1)该市政府2008年投入改善医疗卫生服务的资金是多少万元?
(2)该市政府2009年投入“需方”和“供方”的资金各多少万元?
(3)该市政府预计2011年将有7260万元投入改善医疗卫生服务,若
从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年
的年增长率.二、自定义题怎么考?新知识型题 新知识型题是指材料中给出了新的运算法则或某一数学公式的推导与示例应用,要求学生类比应用该公式或法则解决相关问题的一类试题.材料中的法则或公式有的直接给出,也有的通过问题归纳得出,它们一般是现阶段学生未学到的知识或方法,其目的是考查学生的理解、归纳、类比迁移、主动获取新知识的能力.解答此类题目的关键是阅读题目中介绍的新知识(包括定义、公式、方法、解题思路等),然后运用这些知识去解决新问题. 定义新概念解题关键是理解新定义,再结合已学知识解答.定义新法则定义新图形14.(2015·淄博)如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,求这个“果圆”被y轴截得的弦CD的长.正确理解新定义的图形,寻找形与数的对应关系.
同课章节目录
