2016区优秀中考数学复习专题专题:(卢有祥)探究型之最值问题(21张PPT)
文档属性
| 名称 | 2016区优秀中考数学复习专题专题:(卢有祥)探究型之最值问题(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 108.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-25 10:11:22 | ||
图片预览





文档简介
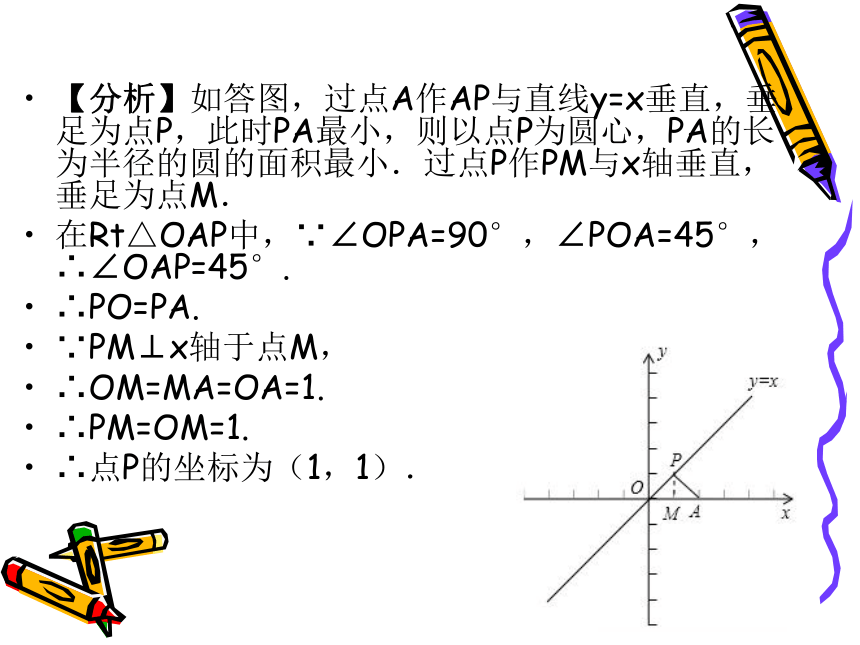
课件21张PPT。专题:探究型之最值问题中兴中学 卢有祥单动点问题 引例:已知点A的坐标为(2,0),点P在直线y=x上运动,当以点P为圆心,PA的长为半径的圆的面积最小时,点P的坐标为【 】【考点】1.单动点问题;
2.一次函数图象上点的坐标特征;
3.垂线段最短的性质;
4.等腰直角三角形的判定和性质;
5.圆的认识.【分析】如答图,过点A作AP与直线y=x垂直,垂足为点P,此时PA最小,则以点P为圆心,PA的长为半径的圆的面积最小.过点P作PM与x轴垂直,垂足为点M.
在Rt△OAP中,∵∠OPA=90°,∠POA=45°,∴∠OAP=45°.
∴PO=PA.
∵PM⊥x轴于点M,
∴OM=MA=OA=1.
∴PM=OM=1.
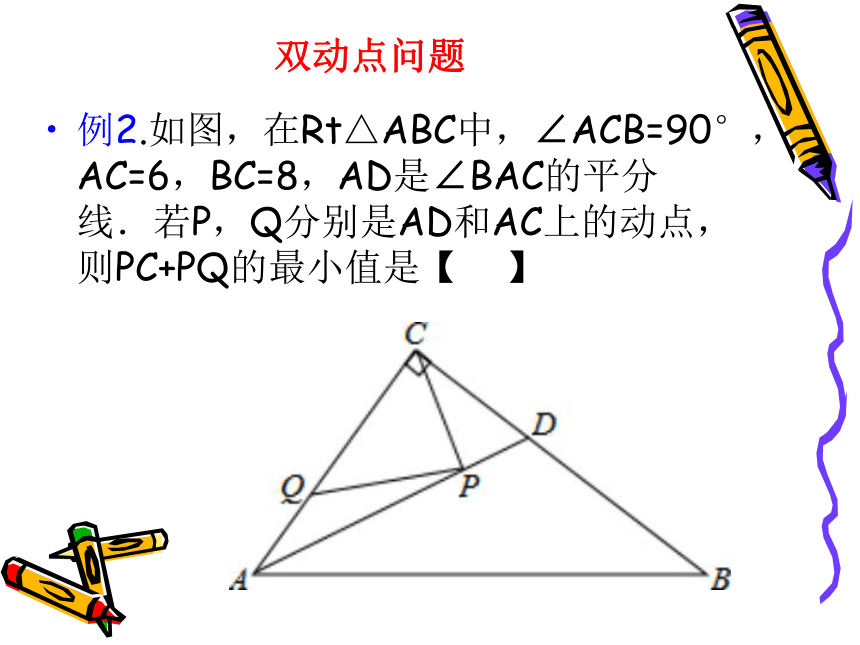
∴点P的坐标为(1,1).例2.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是【 】双动点问题【考点】1.双动点问题;
2.轴对称的应用(最短路线问题);
3.角平分线的性质;
4.勾股定理;
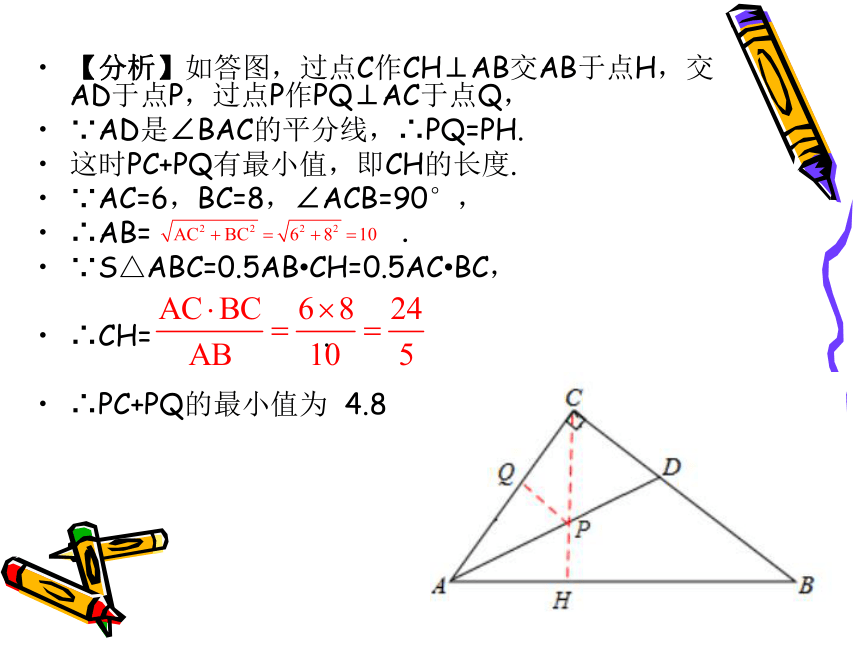
5.直角三角形的面积.【分析】如答图,过点C作CH⊥AB交AB于点H,交AD于点P,过点P作PQ⊥AC于点Q,
∵AD是∠BAC的平分线,∴PQ=PH.
这时PC+PQ有最小值,即CH的长度.
∵AC=6,BC=8,∠ACB=90°,
∴AB= .
∵S△ABC=0.5AB?CH=0.5AC?BC,
∴CH= .
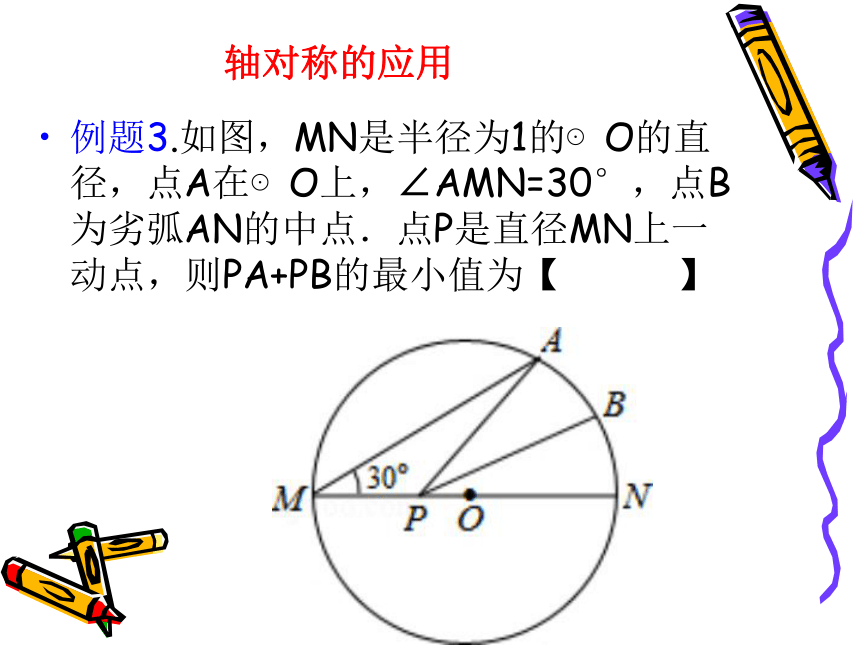
∴PC+PQ的最小值为 4.8 .例题3.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为【 】轴对称的应用【考点】1.轴对称的应用(最短路线问题);2.圆周角定理;3. 等腰直角三角形的判定和性质.
【分析】作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,根据轴对称确定最短路线问题可得AB′与MN的交点即为PA+PB的最小时的点,根据在同圆或等圆中,同弧所对的圆心角等于圆周角的2倍求出∠AON=60°,然后求出∠BON=30°,再根据对称性可得∠B′ON=∠BON=30°,然后求出∠AOB′=90°,从而判断出△AOB′是等腰直角三角形,再根据等腰直角三角形的性质可得AB′=OA,即为PA+PB的最小值:三角形三边关系例题4.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是 ▲ .【考点】1.单动点问题;2.三角形三边关系;3.勾股定理.
【分析】如答图,找到BC的中点O,连接AO,交半圆于P2,在半圆上取P1,连接AP1,OP1,
根据三角形三边关系有AP1+OP1>AE,
∵OP1=OP2,∴AP1>AP2,即AP2是AP的最小值.
∵
∴AP2= .
∴AP的最小值是 .平行四边形的性质例题5.如图,已知点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作ABCD.若AB= ,则平行四边形ABCD面积的最大值为 ▲ .【考点】1.平行四边形的性质;
2. 三角形的面积公式.
【分析】由已知条件,根据平行四边形的性质和三角形的面积公式可知,要使ABCD的面积最大,只要△ABC的面积最大,即当AB、AC是直角边时所求面积最大. 因此,
例题6.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C. 则A′C长度的最小值是 ▲ .【考点】1.单动点和折叠问题;
2.菱形的性质;
3. 锐角三角函数定义;
4.特殊角的三角函数值;
5.三角形边角关系;
6.勾股定理;
7. 折叠对称的性质.【分析】如图1,连接CM,过M点作MH⊥CD交CD的延长线于点H,
则由已知可得,在Rt△DHM中,DM=1,
∠HDM=60°,∴ .∴ .
∴ .
又∵根据翻折对称的性质,A′M=AM=1,
∴△CA′M中,两边一定,要使A′C长度的最小即要∠CM A′最小,此时点A′落在MC上,如图2.
∵M A′=NA=1,∴ .
∴A′C长度的最小值是 .翻折变换(折叠问题) 例题7.如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.则折痕EF的最大值是 ▲ cm.【考点】1.翻折变换(折叠问题);
2.矩形的性质;
3.勾股定理;
4.方程思想的应用.【分析】如答图,当点F与点C重合时,折痕EF最大,
由翻折的性质得,BC=B′C=10cm,
在Rt△B′DC中, cm,
∴AB′=AD﹣B′D=10﹣8=2cm.
设BE=x,则B′E=BE=x,AE=AB﹣BE=6﹣x,
在Rt△AB′E中,AE2+AB′2=B′E2,
即(6﹣x)2+22=x2,解得x= 10/3 .
在Rt△BEF中, cm.最短线路问题例题8.如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.【考点】1.圆的综合题;
2.勾股定理和逆定理;
3.垂径定理;
4.相似三角形的判定和性质;
5.待定系数法的应用;
6.直线上点的坐标与方程的关系;
7.切线的判定;
8.轴对称的应用(最短线路问题).
在Rt△OAP中,∵∠OPA=90°,∠POA=45°,∴∠OAP=45°.
∴PO=PA.
∵PM⊥x轴于点M,
∴OM=MA=OA=1.
∴PM=OM=1.
∴点P的坐标为(1,1).例2.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是【 】双动点问题【考点】1.双动点问题;
2.轴对称的应用(最短路线问题);
3.角平分线的性质;
4.勾股定理;
5.直角三角形的面积.【分析】如答图,过点C作CH⊥AB交AB于点H,交AD于点P,过点P作PQ⊥AC于点Q,
∵AD是∠BAC的平分线,∴PQ=PH.
这时PC+PQ有最小值,即CH的长度.
∵AC=6,BC=8,∠ACB=90°,
∴AB= .
∵S△ABC=0.5AB?CH=0.5AC?BC,
∴CH= .
∴PC+PQ的最小值为 4.8 .例题3.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为【 】轴对称的应用【考点】1.轴对称的应用(最短路线问题);2.圆周角定理;3. 等腰直角三角形的判定和性质.
【分析】作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,根据轴对称确定最短路线问题可得AB′与MN的交点即为PA+PB的最小时的点,根据在同圆或等圆中,同弧所对的圆心角等于圆周角的2倍求出∠AON=60°,然后求出∠BON=30°,再根据对称性可得∠B′ON=∠BON=30°,然后求出∠AOB′=90°,从而判断出△AOB′是等腰直角三角形,再根据等腰直角三角形的性质可得AB′=OA,即为PA+PB的最小值:三角形三边关系例题4.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是 ▲ .【考点】1.单动点问题;2.三角形三边关系;3.勾股定理.
【分析】如答图,找到BC的中点O,连接AO,交半圆于P2,在半圆上取P1,连接AP1,OP1,
根据三角形三边关系有AP1+OP1>AE,
∵OP1=OP2,∴AP1>AP2,即AP2是AP的最小值.
∵
∴AP2= .
∴AP的最小值是 .平行四边形的性质例题5.如图,已知点P是半径为1的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作ABCD.若AB= ,则平行四边形ABCD面积的最大值为 ▲ .【考点】1.平行四边形的性质;
2. 三角形的面积公式.
【分析】由已知条件,根据平行四边形的性质和三角形的面积公式可知,要使ABCD的面积最大,只要△ABC的面积最大,即当AB、AC是直角边时所求面积最大. 因此,
例题6.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C. 则A′C长度的最小值是 ▲ .【考点】1.单动点和折叠问题;
2.菱形的性质;
3. 锐角三角函数定义;
4.特殊角的三角函数值;
5.三角形边角关系;
6.勾股定理;
7. 折叠对称的性质.【分析】如图1,连接CM,过M点作MH⊥CD交CD的延长线于点H,
则由已知可得,在Rt△DHM中,DM=1,
∠HDM=60°,∴ .∴ .
∴ .
又∵根据翻折对称的性质,A′M=AM=1,
∴△CA′M中,两边一定,要使A′C长度的最小即要∠CM A′最小,此时点A′落在MC上,如图2.
∵M A′=NA=1,∴ .
∴A′C长度的最小值是 .翻折变换(折叠问题) 例题7.如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.则折痕EF的最大值是 ▲ cm.【考点】1.翻折变换(折叠问题);
2.矩形的性质;
3.勾股定理;
4.方程思想的应用.【分析】如答图,当点F与点C重合时,折痕EF最大,
由翻折的性质得,BC=B′C=10cm,
在Rt△B′DC中, cm,
∴AB′=AD﹣B′D=10﹣8=2cm.
设BE=x,则B′E=BE=x,AE=AB﹣BE=6﹣x,
在Rt△AB′E中,AE2+AB′2=B′E2,
即(6﹣x)2+22=x2,解得x= 10/3 .
在Rt△BEF中, cm.最短线路问题例题8.如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.【考点】1.圆的综合题;
2.勾股定理和逆定理;
3.垂径定理;
4.相似三角形的判定和性质;
5.待定系数法的应用;
6.直线上点的坐标与方程的关系;
7.切线的判定;
8.轴对称的应用(最短线路问题).
同课章节目录
