2.6.2菱形的判定 课件(共26张PPT)
文档属性
| 名称 | 2.6.2菱形的判定 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-26 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
第一章 直角三角形
2.6.2菱形的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
1.能说出菱形的两个判定定理,并会用它进行相关的论证和计算.
2.会根据已知条件画出菱形.
02
新知导入
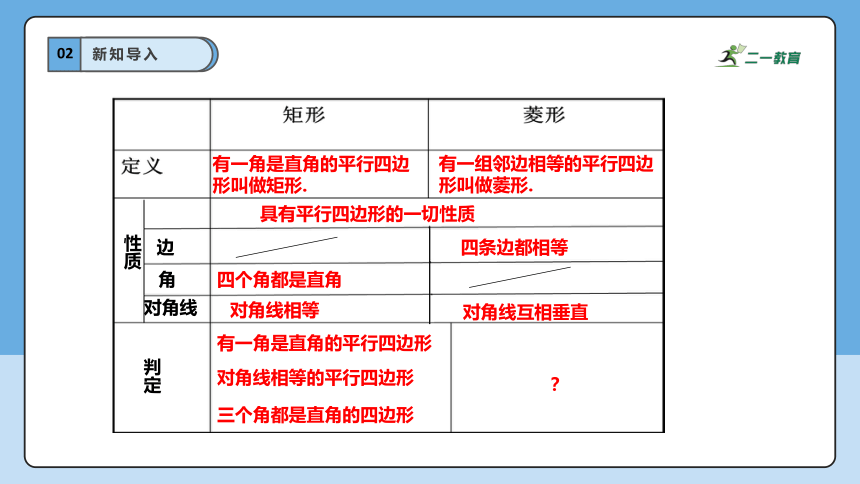
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
具有平行四边形的一切性质
性质
边
角
对角线
四个角都是直角
对角线相等
对角线互相垂直
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
四条边都相等
?
03
新知探究
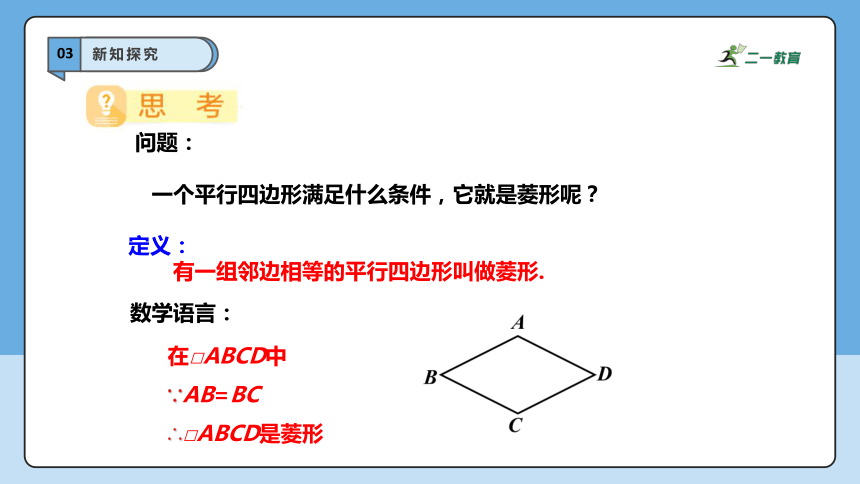
定义:
有一组邻边相等的平行四边形叫做菱形.
一个平行四边形满足什么条件,它就是菱形呢?
在□ABCD中
∵AB=BC
∴□ABCD是菱形
问题:
数学语言:
03
新知探究
动脑筋
如图,用4支长度相等的铅笔能摆成菱形吗?
把上述问题抽象出来就是:
四条边都相等的四边形是菱形吗?
你能证明吗?
03
新知讲解
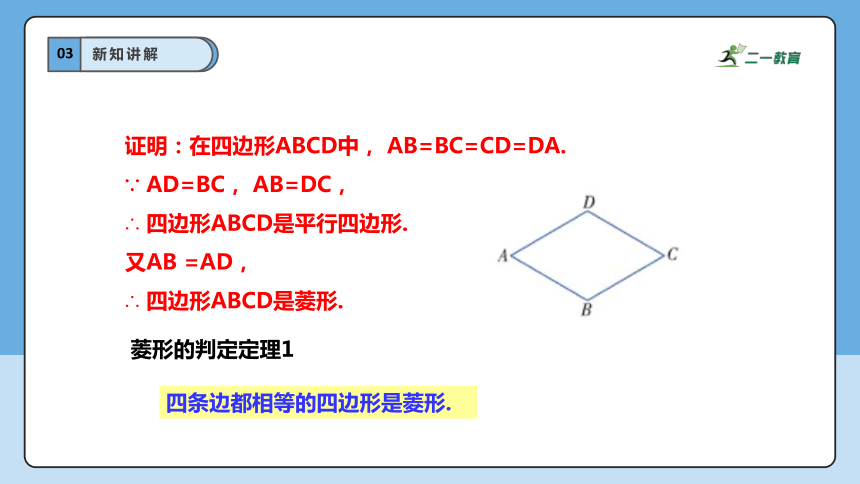
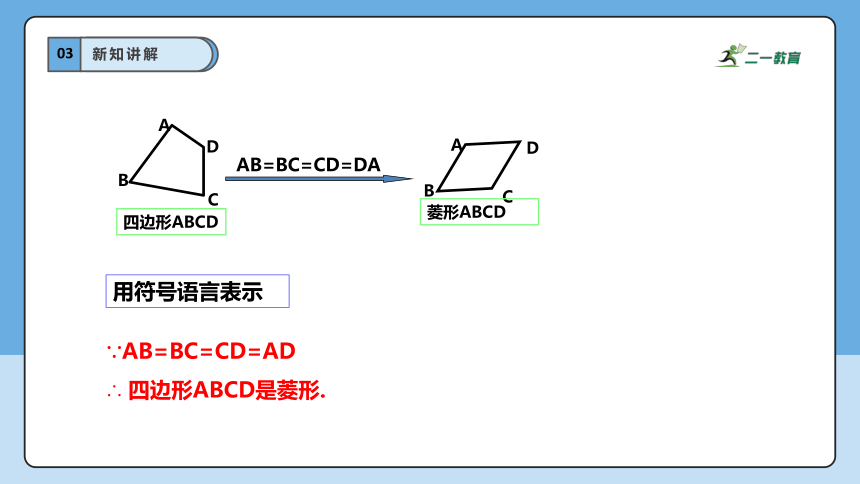
证明:在四边形ABCD中, AB=BC=CD=DA.
∵ AD=BC, AB=DC,
∴ 四边形ABCD是平行四边形.
又AB =AD,
∴ 四边形ABCD是菱形.
菱形的判定定理1
四条边都相等的四边形是菱形.
03
新知讲解
用符号语言表示
∵AB=BC=CD=AD
∴ 四边形ABCD是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
新课探究
例
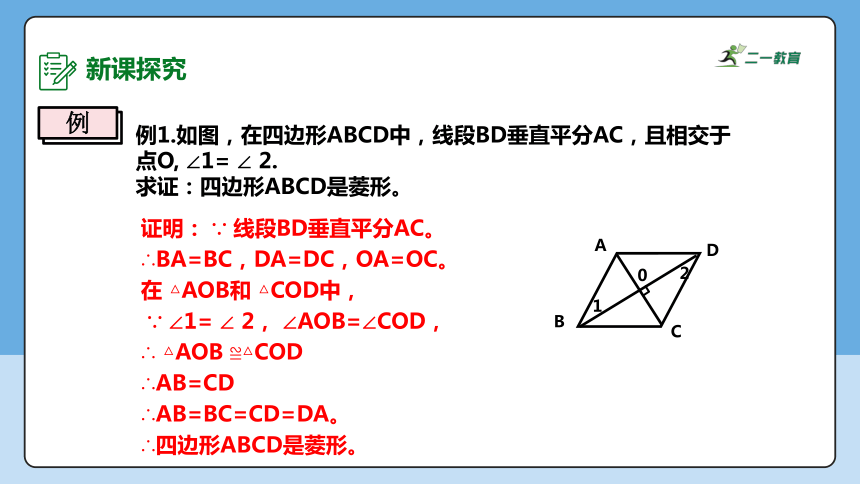
例1.如图,在四边形ABCD中,线段BD垂直平分AC,且相交于点O, ∠1= ∠ 2.
求证:四边形ABCD是菱形。
证明: ∵ 线段BD垂直平分AC。
∴BA=BC,DA=DC,OA=OC。
在 △AOB和 △COD中,
∵ ∠1= ∠ 2, ∠AOB=∠COD,
∴ △AOB ≌△COD
∴AB=CD
∴AB=BC=CD=DA。
∴四边形ABCD是菱形。
A
B
C
D
1
2
0
03
新知讲解
四边形的对角线满足什么条件,它就是菱形呢?
不是,四边形可能是“筝形”
A
B
C
D
问题:
两条对角线互相垂直的四边形是菱形吗?
03
新知讲解
菱形的两条对角线互相垂直且平分,从菱形的这一性质受到启发,你能画出一个菱形吗?
动脑筋
过点O画两条互相垂直的线段AC,BD,使
得OA=OC,OB =OD. 连接AB,BC,CD,DA.
则四边形ABCD是菱形
03
新知讲解
由画法可知,四边形ABCD的两条对角线AC与BD互相平
分,因此它是平行四边形. 又已知其对角线互相垂直,上述问题抽象出来就是:
对角线互相垂直的平行四边形是菱形吗?
你能证明吗?
03
新知讲解
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴□ABCD是菱形。
菱形的判定定理2
对角线互相垂直的平行四边形是菱形.
03
新知讲解
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形。
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
几何语言:
03
新知讲解
例2.如图,在□ABCD中,AC =6,BD=8,AD=5. 求AB的长.
∴ 四边形ABCD是菱形.
∴OA=OC=3 OB=OD=4
解:
又∵AD=5
∴ △ DAO是直角三角形
∴ ∠DOA=90°,即DB ⊥ AC
∴ AB=AD=5.
∵ 四边形ABCD是平行四边形
满足AD2=AO2+DO2
03
新知讲解
命题:每条对角线平分一组对角的四边形是菱形.
已知:在四边形ABCD中,AC分别平分∠BAD和∠BCD,BD分别平分∠ABC和∠ADC。求证:四边形ABCD是菱形
证明:∵AC分别平分∠BAD和∠BCD
∴∠BAC=∠DAC ∠ACB=∠ACD
又∵AC=AC
∴△ABC≌△ADC(ASA)
∴AB=AD BC=DC
同理可证:AB=BC
∴AB=BC=DC=AD
∴四边形ABCD是菱形
注意:这个判定方法不能直接使用
04
课堂练习
【知识技能类作业】必做题:
1.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
04
课堂练习
【知识技能类作业】选做题:
2、如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=______.
25°
04
课堂练习
【综合拓展类作业】
3.如图,四边形ABCD内有一点E,AE=BE=DE=BC=DC,AB=AD,若∠C=100°,则∠AED的大小是多少?
130°
05
课堂小结
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
+邻边相等 =
+对角线线互相垂直=
四条边相等+ =
菱形常用的判定方法
总结:
06
作业布置
【知识技能类作业】必做题:
1.如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的条件是( )
A.BA=BC B.AC,BD互相平分
C.AC=BD D.AB∥CD
B
06
作业布置
【知识技能类作业】选做题:
2.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC,从中选择一个条件使四边形BECF是菱形,你认为这个条件是__________(填序号).
③
06
作业布置
【综合拓展类作业】
3.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N.若∠BAD=∠BCD,AM=AN,求证:四边形ABCD是菱形.
06
作业布置
【综合拓展类作业】
证明:∵AD∥BC, ∴∠BAD+∠B=180°.
∵∠BAD=∠BCD, ∴∠BCD+∠B=180°.
∴AB∥DC.
∴四边形ABCD是平行四边形.
∴∠B=∠D.
∵AM=AN,AM⊥BC,AN⊥DC,
∴Rt△ABM≌Rt△ADN.
∴AB=AD.
∴平行四边形ABCD是菱形.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
2.6.2菱形的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
1.能说出菱形的两个判定定理,并会用它进行相关的论证和计算.
2.会根据已知条件画出菱形.
02
新知导入
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
具有平行四边形的一切性质
性质
边
角
对角线
四个角都是直角
对角线相等
对角线互相垂直
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
四条边都相等
?
03
新知探究
定义:
有一组邻边相等的平行四边形叫做菱形.
一个平行四边形满足什么条件,它就是菱形呢?
在□ABCD中
∵AB=BC
∴□ABCD是菱形
问题:
数学语言:
03
新知探究
动脑筋
如图,用4支长度相等的铅笔能摆成菱形吗?
把上述问题抽象出来就是:
四条边都相等的四边形是菱形吗?
你能证明吗?
03
新知讲解
证明:在四边形ABCD中, AB=BC=CD=DA.
∵ AD=BC, AB=DC,
∴ 四边形ABCD是平行四边形.
又AB =AD,
∴ 四边形ABCD是菱形.
菱形的判定定理1
四条边都相等的四边形是菱形.
03
新知讲解
用符号语言表示
∵AB=BC=CD=AD
∴ 四边形ABCD是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
新课探究
例
例1.如图,在四边形ABCD中,线段BD垂直平分AC,且相交于点O, ∠1= ∠ 2.
求证:四边形ABCD是菱形。
证明: ∵ 线段BD垂直平分AC。
∴BA=BC,DA=DC,OA=OC。
在 △AOB和 △COD中,
∵ ∠1= ∠ 2, ∠AOB=∠COD,
∴ △AOB ≌△COD
∴AB=CD
∴AB=BC=CD=DA。
∴四边形ABCD是菱形。
A
B
C
D
1
2
0
03
新知讲解
四边形的对角线满足什么条件,它就是菱形呢?
不是,四边形可能是“筝形”
A
B
C
D
问题:
两条对角线互相垂直的四边形是菱形吗?
03
新知讲解
菱形的两条对角线互相垂直且平分,从菱形的这一性质受到启发,你能画出一个菱形吗?
动脑筋
过点O画两条互相垂直的线段AC,BD,使
得OA=OC,OB =OD. 连接AB,BC,CD,DA.
则四边形ABCD是菱形
03
新知讲解
由画法可知,四边形ABCD的两条对角线AC与BD互相平
分,因此它是平行四边形. 又已知其对角线互相垂直,上述问题抽象出来就是:
对角线互相垂直的平行四边形是菱形吗?
你能证明吗?
03
新知讲解
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴□ABCD是菱形。
菱形的判定定理2
对角线互相垂直的平行四边形是菱形.
03
新知讲解
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形。
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
几何语言:
03
新知讲解
例2.如图,在□ABCD中,AC =6,BD=8,AD=5. 求AB的长.
∴ 四边形ABCD是菱形.
∴OA=OC=3 OB=OD=4
解:
又∵AD=5
∴ △ DAO是直角三角形
∴ ∠DOA=90°,即DB ⊥ AC
∴ AB=AD=5.
∵ 四边形ABCD是平行四边形
满足AD2=AO2+DO2
03
新知讲解
命题:每条对角线平分一组对角的四边形是菱形.
已知:在四边形ABCD中,AC分别平分∠BAD和∠BCD,BD分别平分∠ABC和∠ADC。求证:四边形ABCD是菱形
证明:∵AC分别平分∠BAD和∠BCD
∴∠BAC=∠DAC ∠ACB=∠ACD
又∵AC=AC
∴△ABC≌△ADC(ASA)
∴AB=AD BC=DC
同理可证:AB=BC
∴AB=BC=DC=AD
∴四边形ABCD是菱形
注意:这个判定方法不能直接使用
04
课堂练习
【知识技能类作业】必做题:
1.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
04
课堂练习
【知识技能类作业】选做题:
2、如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=______.
25°
04
课堂练习
【综合拓展类作业】
3.如图,四边形ABCD内有一点E,AE=BE=DE=BC=DC,AB=AD,若∠C=100°,则∠AED的大小是多少?
130°
05
课堂小结
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
+邻边相等 =
+对角线线互相垂直=
四条边相等+ =
菱形常用的判定方法
总结:
06
作业布置
【知识技能类作业】必做题:
1.如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的条件是( )
A.BA=BC B.AC,BD互相平分
C.AC=BD D.AB∥CD
B
06
作业布置
【知识技能类作业】选做题:
2.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC,从中选择一个条件使四边形BECF是菱形,你认为这个条件是__________(填序号).
③
06
作业布置
【综合拓展类作业】
3.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N.若∠BAD=∠BCD,AM=AN,求证:四边形ABCD是菱形.
06
作业布置
【综合拓展类作业】
证明:∵AD∥BC, ∴∠BAD+∠B=180°.
∵∠BAD=∠BCD, ∴∠BCD+∠B=180°.
∴AB∥DC.
∴四边形ABCD是平行四边形.
∴∠B=∠D.
∵AM=AN,AM⊥BC,AN⊥DC,
∴Rt△ABM≌Rt△ADN.
∴AB=AD.
∴平行四边形ABCD是菱形.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
