3.3 幂函数 课件(共24张PPT)
文档属性
| 名称 | 3.3 幂函数 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-26 12:46:29 | ||
图片预览








文档简介
(共24张PPT)
幂函数
年 级:高一 学 科:数学(人教A版)
幂函数
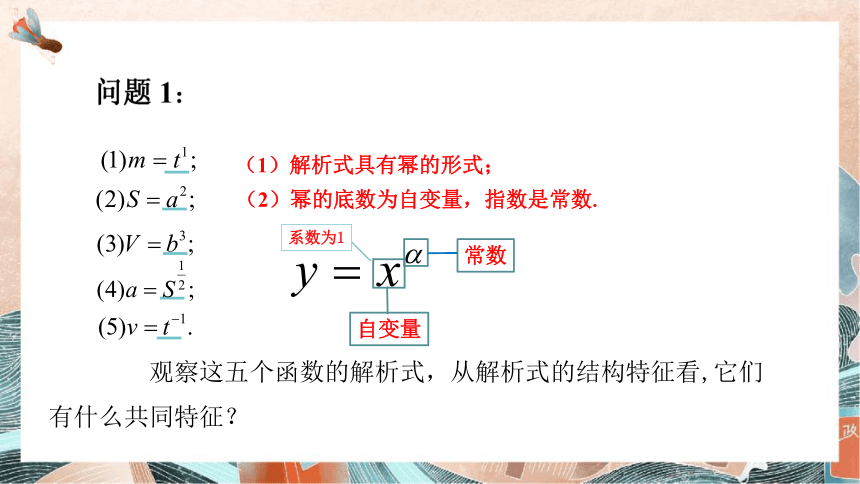
观察这五个函数的解析式,从解析式的结构特征看,它们有什么共同特征?
(1)解析式具有幂的形式;
观察这五个函数的解析式,从解析式的结构特征看,它们有什么共同特征?
(2)幂的底数为自变量,指数是常数,且系数为1.
(1)解析式具有幂的形式;
常数
自变量
(2)幂的底数为自变量,指数是常数.
观察这五个函数的解析式,从解析式的结构特征看,它们有什么共同特征?
系数为1
观察这五个函数的解析式,从解析式的结构特征看,它们有什么共同特征?
追问:你能根据幂函数概念举出一些幂函数的例子吗?
例 (1)下列函数中是幂函数的有
A.y= B.y=2x2
C.y=x2+x D.y=1
√
(2)已知y=(m2+2m-2)x+2n-3是幂函数,求m,n的值.
解:
幂函数
… -2 -1 0 1 2 3 4 …
… …
… …
-8
-1
0
1
8
27
0
1
0
x
y
1
2
3
4
-1
-2
-3
2
4
6
8
-2
-4
-6
-8
y=x3
/
/
64
y=
x
2
4
3
2
1
-1
-2
-3
-4
-2
2
4
6
(1,1)
(2,4)
(-2,4)
(-1,1)
(-1,-1)
y=x
注意:可以从以下角度观察
(1)图象分布的区域,公共点;
(2)函数的对称性;
(3)函数的变化趋势.
共性
共性
代数角度:f(1)=1
共性
奇偶性的不同
单调性的不同
共性
奇偶性的不同
单调性的不同
共性
奇偶性的不同
奇函数
奇函数
奇函数
偶函数
非奇非偶函数
增函数
增函数
增函数
在[0,+∞)上单调递增,在(-∞,0]上单调递减
在[0,+∞)上单调递减,在(-∞,0]上单调递减
解:设 ,代入点 (9,3),可得 ,所以
探究1.已知幂函数 的图象经过点(9,3),则f(100)=__。
探究2:利用幂函数的性质,判断下列各值的大小。
(1)5.20.5 与 5.30.5
(2)0.2-3.5与 0.3-3.5
解:(1)y= x0.5在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.5 < 5.30.5
(2)y=x-3.5在(0,+∞)内是减函数
∵0.2<0.3∴ 0.2-3.5 >0.3-3.5
归纳总结
知识上:幂函数的定义、幂函数的图像与性质;
方法上:数学结合、由特殊到一般;
研究新函数的步骤:明确函数的概念及定义域 探究函数的图象与性质 函数的应用。
课后作业
写一个关于幂函数的小论文.
幂函数
年 级:高一 学 科:数学(人教A版)
幂函数
观察这五个函数的解析式,从解析式的结构特征看,它们有什么共同特征?
(1)解析式具有幂的形式;
观察这五个函数的解析式,从解析式的结构特征看,它们有什么共同特征?
(2)幂的底数为自变量,指数是常数,且系数为1.
(1)解析式具有幂的形式;
常数
自变量
(2)幂的底数为自变量,指数是常数.
观察这五个函数的解析式,从解析式的结构特征看,它们有什么共同特征?
系数为1
观察这五个函数的解析式,从解析式的结构特征看,它们有什么共同特征?
追问:你能根据幂函数概念举出一些幂函数的例子吗?
例 (1)下列函数中是幂函数的有
A.y= B.y=2x2
C.y=x2+x D.y=1
√
(2)已知y=(m2+2m-2)x+2n-3是幂函数,求m,n的值.
解:
幂函数
… -2 -1 0 1 2 3 4 …
… …
… …
-8
-1
0
1
8
27
0
1
0
x
y
1
2
3
4
-1
-2
-3
2
4
6
8
-2
-4
-6
-8
y=x3
/
/
64
y=
x
2
4
3
2
1
-1
-2
-3
-4
-2
2
4
6
(1,1)
(2,4)
(-2,4)
(-1,1)
(-1,-1)
y=x
注意:可以从以下角度观察
(1)图象分布的区域,公共点;
(2)函数的对称性;
(3)函数的变化趋势.
共性
共性
代数角度:f(1)=1
共性
奇偶性的不同
单调性的不同
共性
奇偶性的不同
单调性的不同
共性
奇偶性的不同
奇函数
奇函数
奇函数
偶函数
非奇非偶函数
增函数
增函数
增函数
在[0,+∞)上单调递增,在(-∞,0]上单调递减
在[0,+∞)上单调递减,在(-∞,0]上单调递减
解:设 ,代入点 (9,3),可得 ,所以
探究1.已知幂函数 的图象经过点(9,3),则f(100)=__。
探究2:利用幂函数的性质,判断下列各值的大小。
(1)5.20.5 与 5.30.5
(2)0.2-3.5与 0.3-3.5
解:(1)y= x0.5在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.5 < 5.30.5
(2)y=x-3.5在(0,+∞)内是减函数
∵0.2<0.3∴ 0.2-3.5 >0.3-3.5
归纳总结
知识上:幂函数的定义、幂函数的图像与性质;
方法上:数学结合、由特殊到一般;
研究新函数的步骤:明确函数的概念及定义域 探究函数的图象与性质 函数的应用。
课后作业
写一个关于幂函数的小论文.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
