2.7正方形 课件（共31张PPT）

(共31张PPT)
第一章 直角三角形
2.7正方形
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
1．了解正方形的有关概念，理解并掌握正方形的性质、判定方法．
2．发展推理能力，逐步掌握说理的基本方法．
02
新知导入
　除了矩形和菱形外，还有什么特殊的平行四边形吗？　　　
正方形　
　怎样研究这类图形？
　先看看我们是怎样研究矩形和菱形的.
03
新知探究
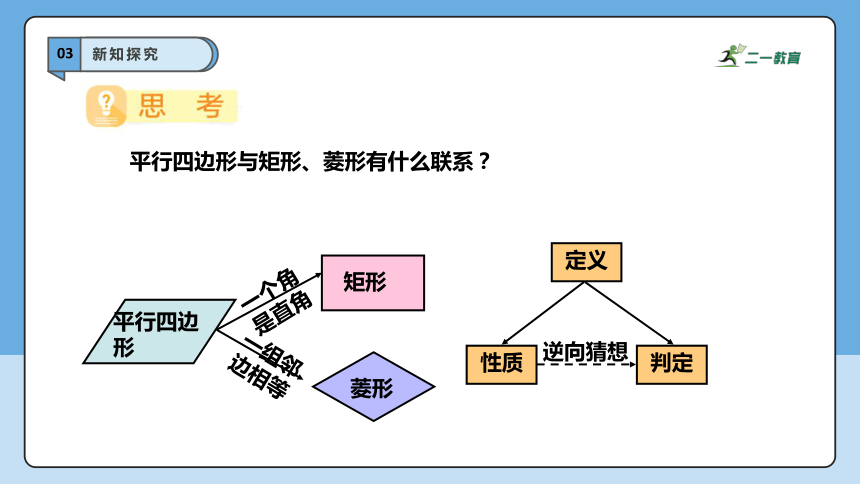
平行四边形与矩形、菱形有什么联系？
性质
定义
判定
逆向猜想
一个角
是直角　
一组邻
边相等　　
平行四边形 　
矩形 　
菱形 　
03
新知探究
观察
装修房子铺地面的瓷砖大多是正方形的形状， 它是什么样的四边形呢？ 它与平行四边形、矩形、菱形有什么关系？
03
新知讲解
正方形的四条边都相
等， 四个角都是直角.
正方形既是矩形又是菱形.
03
新知讲解
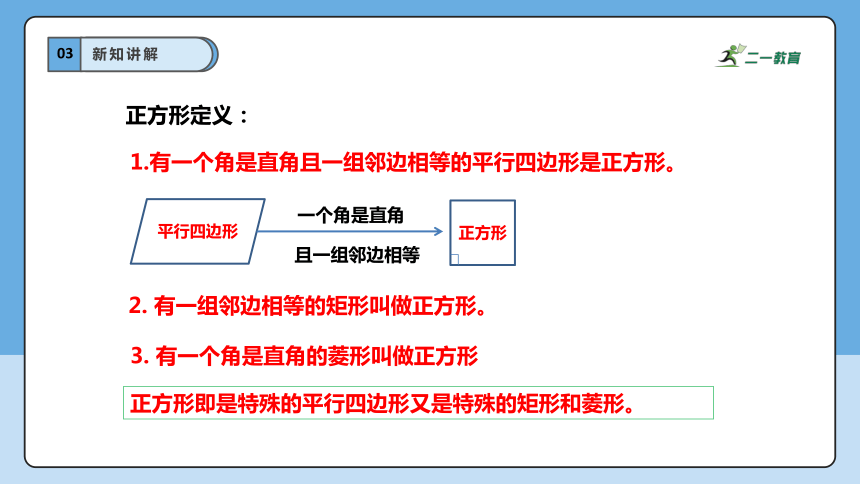
正方形定义：
3. 有一个角是直角的菱形叫做正方形
1.有一个角是直角且一组邻边相等的平行四边形是正方形。
2. 有一组邻边相等的矩形叫做正方形。
平行四边形
一个角是直角
且一组邻边相等
正方形
正方形即是特殊的平行四边形又是特殊的矩形和菱形。
03
新知讲解
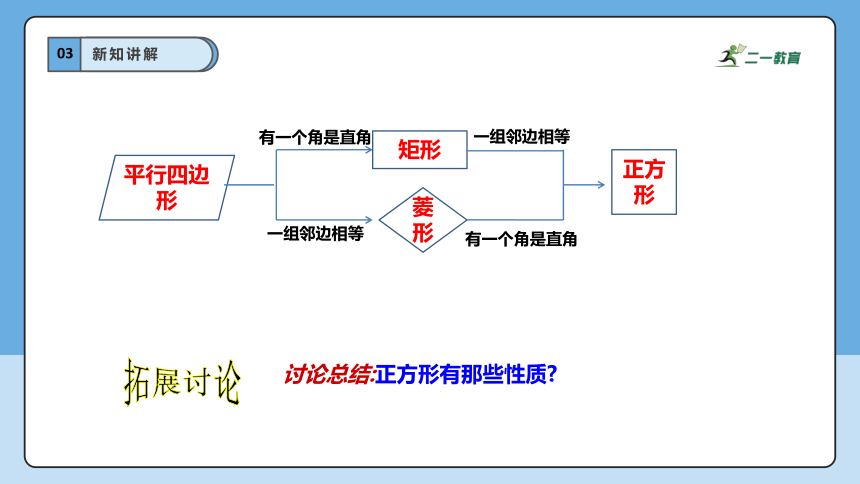
平行四边形
矩形
菱形
正方形
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
讨论总结:正方形有那些性质
拓展讨论
03
新知讲解
正方形是特殊的平行四边形，也是特殊的矩形，也是特殊的菱形。

正方形的性质=
菱形性质
矩形性质
03
新知讲解
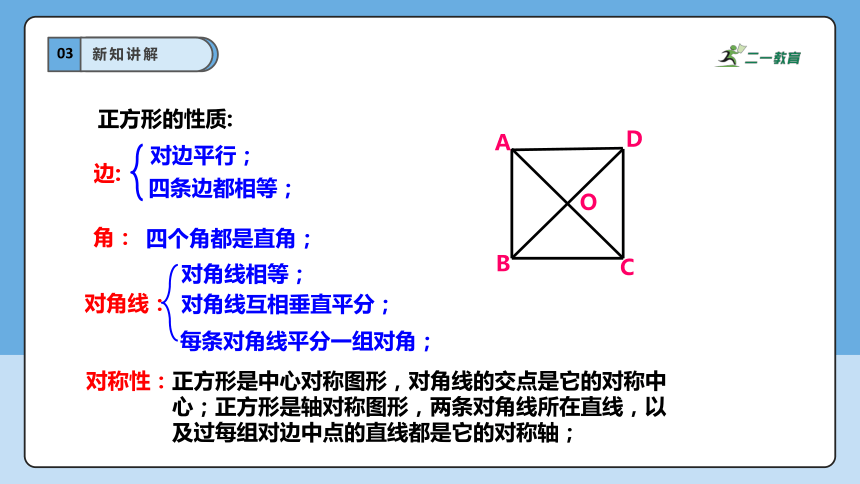
正方形的性质:
O
A
B
C
D
边:
对边平行；
四条边都相等；
四个角都是直角；
对角线相等；
对角线互相垂直平分；
每条对角线平分一组对角；
正方形是中心对称图形，对角线的交点是它的对称中心；正方形是轴对称图形，两条对角线所在直线，以及过每组对边中点的直线都是它的对称轴；
角：
对角线：
对称性：
新课探究
例
例1.如图，点E 是正方形ABCD的边AB上任意一点，过点D 作DF⊥DE交BC的延长线于点F.求证：DE = DF.
证明∵ 四边形ABCD为正方形，
∴ AD=CD， ∠A=∠DCF= 90°.
∵ DF⊥DE，
∴ ∠EDF= 90°， 即∠1+∠3 =90°，
又∵ ∠2+∠3= 90°，
∴ ∠1=∠2.
∴ △AED≌△CFD （ASA）.
∴ DE=DF.
03
新知讲解
你能否利用手中的矩形白纸裁出一个正方形呢？请你与同学交流一下，你能说说矩形与正方形的关系吗？
动手操作
总结：矩形+( )=正方形
有一组邻
边相等
一组邻边相等
03
新知讲解
有一组邻边相等的矩形是正方形.
∵矩形ABCD中，AB=BC
∴ABCD为正方形
你能从这个变化过程中总结出一种正方形的判定方法吗？
03
新知讲解
想一想
可以活动的菱形模型能变成一个正方形吗？如何变？
总结：菱形+( )=正方形
有一个角
是直角
一个角是直角
03
新知讲解
你能从这个变化过程中总结出一种正方形的判定方法吗？
有一个角是直角的菱形是正方形.
∵菱形ABCD中，∠A=90°
∴ABCD为正方形
03
新知讲解
思考：如果是平行四边形呢？
有一组邻
边相等
有一个角
是直角
有一个角
是直角
有一组邻
边相等
总结：平行四边形+( )+( )=正方形
有一组邻
边相等
有一个角
是直角
03
新知讲解
你能从这个变化过程中总结出一种正方形的判定方法吗？
有一个角是直角且一组邻边相等的平行四边形叫做正方形
∵□ABCD中，AB=BC且∠A=90°
∴ABCD为正方形
03
新知讲解
正方形的判定
我们把有一组邻边相等且有一个角是直角的平行四边形叫作正方形
有一个角是直角的菱形是正方形。
有一组邻边相等的矩形是正方形。
定义法
菱形法
矩形法
03
新知讲解
例2 如图,已知点A′，B′，C′，D′分别是正方形ABCD 四条边上的点，并且AA′ =BB′ =CC′ =DD′.
求证：四边形A′B′C′D′是正方形.
03
新知讲解
证明∵ 四边形ABCD是正方形，
∴ AB=BC=CD=DA.
又∵ AA′=BB′=CC′=DD′，
∴ D′A=A′B=B′C=C′D.
又∵ ∠A=∠B=∠C=∠D= 90°，
∴ △AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
∴ A′D′= B′A′= C′B′= D′C′.
∴ 四边形A′B′C′D′是菱形.
04
课堂练习
【知识技能类作业】必做题：
1.已知四边形ABCD中，∠A=∠B=∠C=90°，如果再添加一个条件，即可推出该四边形是正方形，那么这个条件可以是( )
A.∠D=90° B.AB＝CD C.AD=BC D.BC=CD
D
04
课堂练习
【知识技能类作业】选做题：
2.如图，在正方形ABCD的外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为多少度？
60°
04
课堂练习
【综合拓展类作业】
4、如图，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是多少.
05
课堂小结
平行四边形
矩形
四边形
菱形
正
方
形
四边形与特殊四边形的关系
06
作业布置
【知识技能类作业】必做题：
1.在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是( )
A.AC=BD，AB∥CD，AB=CD B.AD∥BC，∠A=∠C
C.AO=BO=CO=DO，AC⊥BD
D.AO=CO，BO=DO，AB=BC
C
06
作业布置
【知识技能类作业】选做题：
2.如图，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC的周长为12，则EC的长为__________.
5
06
作业布置
【综合拓展类作业】
3.如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°后至△DBE，再把△ABC沿射线AB平移至△FEG，DE，FG相交于点H.
(1)判断线段DE、FG的位置关系，并说明理由；
(2)连接CG，求证：四边形CBEG是正方形.
06
作业布置
【综合拓展类作业】
解：(1)DE⊥FG，
理由如下：由题意得∠A=∠EDB=∠GFE，∠ABC=∠DBE=90°，
∴∠BDE+∠BED=90°.
∴∠GFE+∠BED=90°.
∴∠FHE=90°，即DE⊥FG.
(2)证明：
∵△ABC沿射线AB平移至△FEG，
∴CB∥GE，CB=GE.
∴四边形CBEG是平行四边形.
∵∠ABC=∠GEF=90°，
∴四边形CBEG是矩形.
∵BC=BE，
∴四边形CBEG是正方形.
Thanks!
https://www.21cnjy.com/recruitment/home/fine