江苏省仪征市2024-2025学年八年级上学期期末考试数学试卷(图片版,含答案)
文档属性
| 名称 | 江苏省仪征市2024-2025学年八年级上学期期末考试数学试卷(图片版,含答案) |  | |
| 格式 | |||
| 文件大小 | 710.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-27 17:10:57 | ||
图片预览




文档简介
江苏省仪征市 2024-2025 学年八年级上学期期末考试数学试卷
一、选择题:本题共 8 小题,每小题 3 分,共 24 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.数学中有许多精美的曲线,以下是“三叶玫瑰线”“笛卡尔叶形线”“星形线”和“阿基米德螺线”,
其中不是轴对称图形的是( )
A. B. C. D.
2.68400精确到千位的近似值为( )
A. 6.8 B. 6.9 C. 6.8 × 104 D. 6.9 × 104
3.若正比例函数的图像经过点(1,3),则这个图像必经过点( )
A. (1, 3) B. ( 1,3) C. ( 1, 3) D. (3,1)
4.根据下列已知条件,则 形状和大小能完全确定的是( )
A. ∠ = 90 , ∠ = 30 B. = 3, = 4
C. = 3, = 4, ∠ = 40 D. ∠ = 30 , ∠ = 45 , = 3
5.已知一次函数 = + 3,那么下列结论正确的是( )
A. 图像经过第一、二、四象限 B. 随 的增大而增大
C. 当 > 0时, < 3 D. 点(1,4)在函数图像上
6.如果三角形三条边的垂直平分线的交点落在三角形的边上,这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等边三角形
7.如图,在 中,∠ = 90 , 为斜边 上的中线,过点 作 ⊥ ,连接 、 ,若 =
8, = 10,则 的长为( )
A. 6 B. 8 C. 10 D. 12
第 1 页,共 13 页
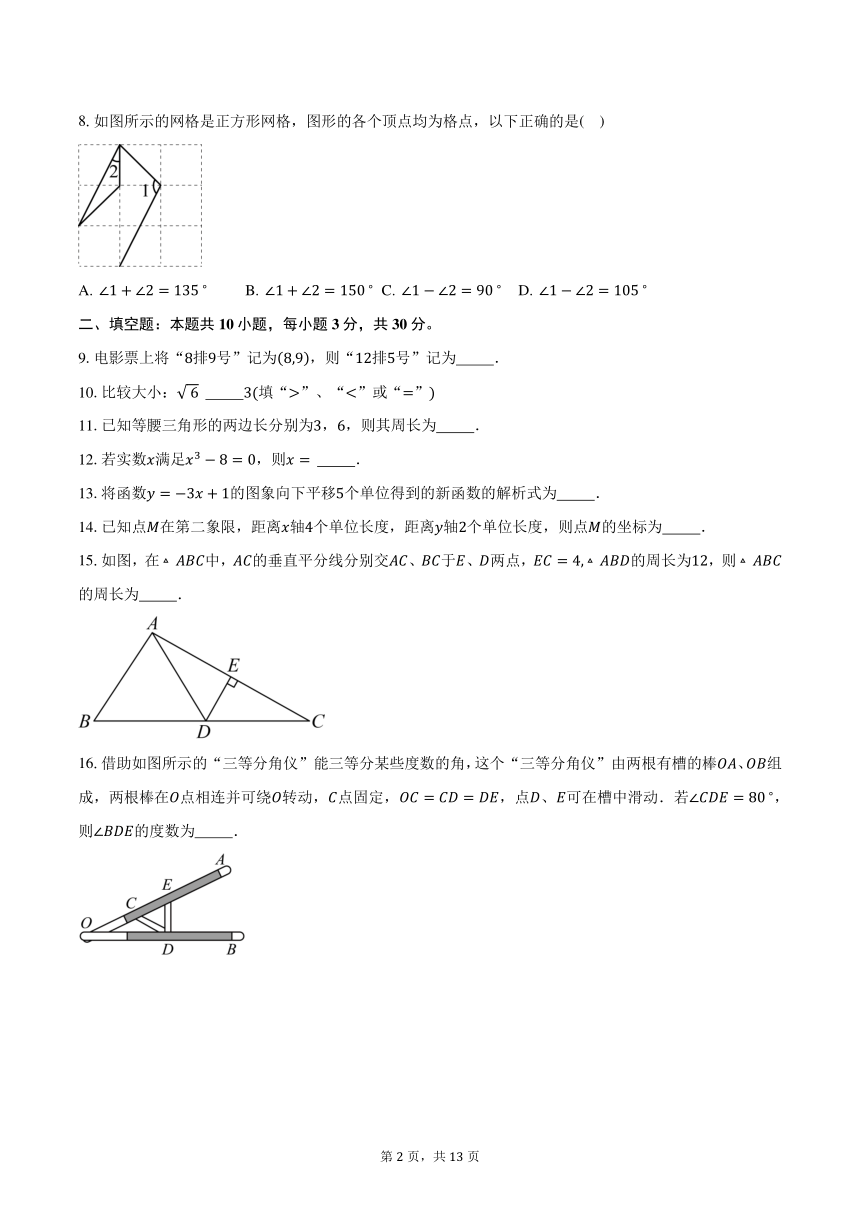
8.如图所示的网格是正方形网格,图形的各个顶点均为格点,以下正确的是( )
A. ∠1 + ∠2 = 135 B. ∠1 + ∠2 = 150 C. ∠1 ∠2 = 90 D. ∠1 ∠2 = 105
二、填空题:本题共 10 小题,每小题 3 分,共 30 分。
9.电影票上将“8排9号”记为(8,9),则“12排5号”记为 .
10.比较大小:√ 6 3(填“>”、“<”或“=”)
11.已知等腰三角形的两边长分别为3,6,则其周长为 .
12.若实数 满足 3 8 = 0,则 = .
13.将函数 = 3 + 1的图象向下平移5个单位得到的新函数的解析式为 .
14.已知点 在第二象限,距离 轴4个单位长度,距离 轴2个单位长度,则点 的坐标为 .
15.如图,在 中, 的垂直平分线分别交 、 于 、 两点, = 4, 的周长为12,则
的周长为 .
16.借助如图所示的“三等分角仪”能三等分某些度数的角,这个“三等分角仪”由两根有槽的棒 、 组
成,两根棒在 点相连并可绕 转动, 点固定, = = ,点 、 可在槽中滑动.若∠ = 80 ,
则∠ 的度数为 .
第 2 页,共 13 页
17.如图,等腰 和等腰△ 满足 = = = ,底边 、 落在同一条直线上,且 ⊥
于点 ,若 = 12, = 16,则 = .
18.直线 = + 1与直线 = 2 的图像如图,若点 是直线 = + 1图像上一点,点 是直线 = 2 图
像上一点,满足 // 轴,且 = 4,则点 坐标为 .
三、解答题:本题共 10 小题,共 80 分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
如图,点 、 在线段 上, = , // , = .求证: = .
20.(本小题8分)
已知一次函数 = + 1的图像经过点(1,3).
(1)求这个一次函数的解析式;
(2)若点( , 5)也在这个函数的图像上,求 的值.
21.(本小题8分)
如图,在 中,∠ = 90 , ∠ = 40 , 为 上一点, ⊥ 于点 ,若 = ,求∠ 度数.
22.(本小题8分)
第 3 页,共 13 页
观察下面图形,每个小正方形的边长为1.
(1)图中阴影正方形的面积是 ,边长是 ;
(2)请用无刻度的直尺和圆规在右图的数轴上作出点 ,使得点 表示的数为√ 13(保留作图痕迹,不写作法
).
23.(本小题8分)
如图, 中, 的垂直平分线 交 于点 ,交 于点 , 为 中点, = .
(1)求证: ⊥ ;
(2)若∠ = 36 ,求∠ 的度数.
24.(本小题8分)
小可的妈妈打算购买一些草莓回家做水果拼盘,经了解,生态园区中的“老农果园”的草莓标价为50元/千
克,若一次性购买不超过2千克,则按原价付款,若购买超过2千克,则超过部分按标价的八折付款.
(1)请求出付款金额 (元)关于购买草莓的重量 (千克)的函数表达式( > 2);
(2)去购买草莓当天,发现旁边的“盛田果园”也在进行草莓优惠活动,同品种草莓标价也为50元/千克,
但全部按标价的九折付款,小可妈妈计划用200元购买此种草莓(全部用完),请问她在哪个果园购买更合
算?
25.(本小题8分)
5
如图,点 、 是直线 上两点,且 = √ 5, = ,在线段 上取一点 ,经测量, = 2, = 1.
2
第 4 页,共 13 页
(1) 长是否为点 到直线 的最短距离?请说明理由;
(2)求点 和点 的距离.
26.(本小题8分)
在平面直角坐标系中,设一次函数 1 = + 、 2 = + ( 、 是实数,且 ≠ 0.
(1)若 = 2, = 3,分别求出 1、 2与 轴的交点坐标;
(2)若函数 1的图像与 轴交点坐标为(5,0),则函数 2的图像与 轴交点坐标为 ;
(3)若函数 1的图像不经过第一象限,且过点(1, 4),求 的取值范围.
27.(本小题8分)
如图1,在 中,∠ = 90 ,已知 = 3, = 4, 是边 上一动点,连接 ,以 为对称轴
将 翻折至 ′ .
(1)当 ′// 时,求 的长;
(2)当 ′落在线段 上时.在图2中补全图形,并求出 的长;
(3)当 ′ ⊥ 时,如图3,求出 的长.
28.(本小题8分)
在平面直角坐标系 中,点 , 分别在 轴, 轴正半轴上,如果在第一象限存在点 使得 = ,且点
在直线 的右侧,则称点 是线段 的“等腰点”,已知点 是线段 的“等腰点”.
第 5 页,共 13 页
(1)如图1,已知 (1,0)、 (0,1),则在坐标(1,1)、(1,2)、(2,1)中,能够是线段 的“等腰点”的点 是 ,
此时 长为 ;
(2)如图2,已知 (3,0)、 (0,4),且∠ = 90 ,求“等腰点”点 的坐标;
(3)如图3,已知 ( , 0)、 (0, ),满足 2 + 2 = 4,且∠ = 60 ,直接写出 的最大值.
第 6 页,共 13 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】(12,5)
10.【答案】<
11.【答案】15
12.【答案】2
13.【答案】 = 3 4
/ = 4 3
14.【答案】( 2,4)
15.【答案】20
16.【答案】75
17.【答案】50
5 2
18.【答案】(1,2)或( , )
3 3
19.【答案】证明:∵ // ,
∴ ∠ = ∠ ,
在 和 中,
=
{∠ = ∠ ,
=
∴ ≌ ( ),
∴ = .
20.【答案】【小题1】
第 7 页,共 13 页
解:∵一次函数 = + 1的图像经过点(1,3),
∴ 3 = + 1,
解得 = 2,
∴这个一次函数的解析式为 = 2 + 1;
【小题2】
解:∵点( , 5)在函数 = 2 + 1的图像上,
∴ 5 = 2 + 1,
解得 = 2.
21.【答案】解:∵ ⊥ 于点 ,
∴ ∠ = ∠ = 90 ,
∵ = , = ,
∴ ≌ ( )
∴ ∠ = ∠ ,
∵ ∠ = 90 , ∠ = 40 ,
1
∴ ∠ = × (180 90 40 ) = 25
2
∴ ∠ = 180 90 25 = 65 .
22.【答案】【小题1】
13
√ 13
【小题2】
解:如图,点 表示的数为√ 13.
23.【答案】【小题1】
如图,连接 ,
第 8 页,共 13 页
∵ 的垂直平分线 交 于点 ,
∴ =
∵ =
∴ = ,
∵ 为 中点,
∴ ⊥ ;
【小题2】
∵ = ,∠ = 36
∴ ∠ = ∠ = 36
∴ ∠ = ∠ + ∠ = 72
∵ =
∴ ∠ = ∠ = 72
∴ ∠ = 180 ∠ ∠ = 72 .
24.【答案】【小题1】
解:由题意得, = 2 × 50 + 50 × 0.8( 2) = 40 + 20;
【小题2】
解:在 = 40 + 20中,当 = 200时, = 4.5;
40
200 ÷ (50 × 0.9) = ,
9
40
∵ < 4.5,
9
∴她在老农果园购买更合算.
25.【答案】【小题1】
解: 长是点 到直线 的最短距离;
理由如下:
∵ = √ 5, = 2, = 1,
第 9 页,共 13 页
∴ 2 + 2 = 12 + 22 = 5 = 2,
∴ 是直角三角形,且∠ = 90 ,
即 ⊥ ,
∴ 长是点 到直线 的最短距离;
【小题2】
解:由(1)知, ⊥ ,
5
在 中, = 2, = ,
2
2 2 3由勾股定理得: = √ = ;
2
3
∴点 和点 的距离为 .
2
26.【答案】【小题1】
解:∵ = 2, = 3,
∴ 1 = 2 3, 2 = 3 + 2,
分别令 1 = 0, 2 = 0代入可得:2 3 = 0, 3 + 2 = 0,
3 2
解得: = , = ,
2 3
3 2
∴ 1、 2与 轴的交点坐标分别为( , 0) , ( , 0); 2 3
【小题2】
1
( , 0)
5
【小题3】
解:由函数 1的图像不经过第一象限,可得 < 0, < 0,
把点(1, 4)代入 2 = + 得: + = 4,
∴ = 4 < 0,
∴ 4 < < 0.
27.【答案】【小题1】
解:∵ ′// ,
∴ ∠ = ∠ ′ ,
∵以 为对称轴将 翻折至 ′ ,
第 10 页,共 13 页
∴ ∠ ′ = ∠ ,
∴ ∠ = ∠ ,
∴ 是等腰三角形,
∴ = = 3.
【小题2】
解:如图,以 为对称轴将 翻折至 ′ ,当 ′落在线段 上时,有 ⊥ , = ′,
∴ ∠ = 90 = ∠ ,
又∵ ∠ = ∠ ,
∴ ∽ ,
∴ = ,
又∵ 是直角三角形, = √ 2 + 2 = √ 32 + 42 = 5,
2 32 9
∴ = = = .
5 5
【小题3】
解:如图:
∵以 为对称轴将 翻折至 ′ ,
∴ = ′,∠ = ∠ ′,
∵ ′ ⊥ ,
∴ ∠ = ∠ ′ = 90 ,
∴ ∠ = ∠ ,
又∵ ∠ = ∠ ,
∴ ∽ ,
第 11 页,共 13 页
∴ = ,
2 42 16
∴ = = = ,
5 5
∵在 ′和△ 中,∠ = ∠ ′,∠ ′ = ∠ ,
∴△ ′ ∽△ ,
∴ = ,即 = ,
′ ′
16
5 4
∴ 5 = ,
5
∴解得 = 1.
28.【答案】【小题1】
(1,1)
√ 2
【小题2】
解:如图所示,过点 作 ⊥ 轴交 轴于 ,过点 作 ⊥ 于 ,则 = , = ,
∵ (3,0)、 (0,4),
∴ = = 4, = 3,
∵点 是线段 的“等腰点”,
∴ = ,
∵ ∠ = 90 , ⊥ 轴, ⊥ ,
∴ ∠ = ∠ = ∠ = 90 ,
∴ ∠ + ∠ = ∠ + ∠ = 90 ,
∴ ∠ = ∠ ,
∴ ≌ ( ),
∴ = = , = ,
∴ = + = + = 4, = = = 3,
7
∴ = ,
2
7
∴ = = = ,
2
7 7
∴ ( , );
2 2
第 12 页,共 13 页
【小题3】
解:如图所示,取 中点 ,连接 , ,
∵点 是线段 的“等腰点”,
∴ = ,
∵ ∠ = 60 ,
∴ 是等边三角形;
∵ ( , 0)、 (0, ),
∴ = , = ,
∴ 2 = 2 + 2 = 2 + 2 = 4,
∴ = = 2,
∵ 为 的中点,∠ = 90 ,
1
∴ = = = 1,
2
∴ = √ 2 2 = √ 3,
∵ ≤ + ,
∴当 、 、 三点共线时, 有最大值,最大值为1 + √ 3.
第 13 页,共 13 页
一、选择题:本题共 8 小题,每小题 3 分,共 24 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.数学中有许多精美的曲线,以下是“三叶玫瑰线”“笛卡尔叶形线”“星形线”和“阿基米德螺线”,
其中不是轴对称图形的是( )
A. B. C. D.
2.68400精确到千位的近似值为( )
A. 6.8 B. 6.9 C. 6.8 × 104 D. 6.9 × 104
3.若正比例函数的图像经过点(1,3),则这个图像必经过点( )
A. (1, 3) B. ( 1,3) C. ( 1, 3) D. (3,1)
4.根据下列已知条件,则 形状和大小能完全确定的是( )
A. ∠ = 90 , ∠ = 30 B. = 3, = 4
C. = 3, = 4, ∠ = 40 D. ∠ = 30 , ∠ = 45 , = 3
5.已知一次函数 = + 3,那么下列结论正确的是( )
A. 图像经过第一、二、四象限 B. 随 的增大而增大
C. 当 > 0时, < 3 D. 点(1,4)在函数图像上
6.如果三角形三条边的垂直平分线的交点落在三角形的边上,这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等边三角形
7.如图,在 中,∠ = 90 , 为斜边 上的中线,过点 作 ⊥ ,连接 、 ,若 =
8, = 10,则 的长为( )
A. 6 B. 8 C. 10 D. 12
第 1 页,共 13 页
8.如图所示的网格是正方形网格,图形的各个顶点均为格点,以下正确的是( )
A. ∠1 + ∠2 = 135 B. ∠1 + ∠2 = 150 C. ∠1 ∠2 = 90 D. ∠1 ∠2 = 105
二、填空题:本题共 10 小题,每小题 3 分,共 30 分。
9.电影票上将“8排9号”记为(8,9),则“12排5号”记为 .
10.比较大小:√ 6 3(填“>”、“<”或“=”)
11.已知等腰三角形的两边长分别为3,6,则其周长为 .
12.若实数 满足 3 8 = 0,则 = .
13.将函数 = 3 + 1的图象向下平移5个单位得到的新函数的解析式为 .
14.已知点 在第二象限,距离 轴4个单位长度,距离 轴2个单位长度,则点 的坐标为 .
15.如图,在 中, 的垂直平分线分别交 、 于 、 两点, = 4, 的周长为12,则
的周长为 .
16.借助如图所示的“三等分角仪”能三等分某些度数的角,这个“三等分角仪”由两根有槽的棒 、 组
成,两根棒在 点相连并可绕 转动, 点固定, = = ,点 、 可在槽中滑动.若∠ = 80 ,
则∠ 的度数为 .
第 2 页,共 13 页
17.如图,等腰 和等腰△ 满足 = = = ,底边 、 落在同一条直线上,且 ⊥
于点 ,若 = 12, = 16,则 = .
18.直线 = + 1与直线 = 2 的图像如图,若点 是直线 = + 1图像上一点,点 是直线 = 2 图
像上一点,满足 // 轴,且 = 4,则点 坐标为 .
三、解答题:本题共 10 小题,共 80 分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
如图,点 、 在线段 上, = , // , = .求证: = .
20.(本小题8分)
已知一次函数 = + 1的图像经过点(1,3).
(1)求这个一次函数的解析式;
(2)若点( , 5)也在这个函数的图像上,求 的值.
21.(本小题8分)
如图,在 中,∠ = 90 , ∠ = 40 , 为 上一点, ⊥ 于点 ,若 = ,求∠ 度数.
22.(本小题8分)
第 3 页,共 13 页
观察下面图形,每个小正方形的边长为1.
(1)图中阴影正方形的面积是 ,边长是 ;
(2)请用无刻度的直尺和圆规在右图的数轴上作出点 ,使得点 表示的数为√ 13(保留作图痕迹,不写作法
).
23.(本小题8分)
如图, 中, 的垂直平分线 交 于点 ,交 于点 , 为 中点, = .
(1)求证: ⊥ ;
(2)若∠ = 36 ,求∠ 的度数.
24.(本小题8分)
小可的妈妈打算购买一些草莓回家做水果拼盘,经了解,生态园区中的“老农果园”的草莓标价为50元/千
克,若一次性购买不超过2千克,则按原价付款,若购买超过2千克,则超过部分按标价的八折付款.
(1)请求出付款金额 (元)关于购买草莓的重量 (千克)的函数表达式( > 2);
(2)去购买草莓当天,发现旁边的“盛田果园”也在进行草莓优惠活动,同品种草莓标价也为50元/千克,
但全部按标价的九折付款,小可妈妈计划用200元购买此种草莓(全部用完),请问她在哪个果园购买更合
算?
25.(本小题8分)
5
如图,点 、 是直线 上两点,且 = √ 5, = ,在线段 上取一点 ,经测量, = 2, = 1.
2
第 4 页,共 13 页
(1) 长是否为点 到直线 的最短距离?请说明理由;
(2)求点 和点 的距离.
26.(本小题8分)
在平面直角坐标系中,设一次函数 1 = + 、 2 = + ( 、 是实数,且 ≠ 0.
(1)若 = 2, = 3,分别求出 1、 2与 轴的交点坐标;
(2)若函数 1的图像与 轴交点坐标为(5,0),则函数 2的图像与 轴交点坐标为 ;
(3)若函数 1的图像不经过第一象限,且过点(1, 4),求 的取值范围.
27.(本小题8分)
如图1,在 中,∠ = 90 ,已知 = 3, = 4, 是边 上一动点,连接 ,以 为对称轴
将 翻折至 ′ .
(1)当 ′// 时,求 的长;
(2)当 ′落在线段 上时.在图2中补全图形,并求出 的长;
(3)当 ′ ⊥ 时,如图3,求出 的长.
28.(本小题8分)
在平面直角坐标系 中,点 , 分别在 轴, 轴正半轴上,如果在第一象限存在点 使得 = ,且点
在直线 的右侧,则称点 是线段 的“等腰点”,已知点 是线段 的“等腰点”.
第 5 页,共 13 页
(1)如图1,已知 (1,0)、 (0,1),则在坐标(1,1)、(1,2)、(2,1)中,能够是线段 的“等腰点”的点 是 ,
此时 长为 ;
(2)如图2,已知 (3,0)、 (0,4),且∠ = 90 ,求“等腰点”点 的坐标;
(3)如图3,已知 ( , 0)、 (0, ),满足 2 + 2 = 4,且∠ = 60 ,直接写出 的最大值.
第 6 页,共 13 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】(12,5)
10.【答案】<
11.【答案】15
12.【答案】2
13.【答案】 = 3 4
/ = 4 3
14.【答案】( 2,4)
15.【答案】20
16.【答案】75
17.【答案】50
5 2
18.【答案】(1,2)或( , )
3 3
19.【答案】证明:∵ // ,
∴ ∠ = ∠ ,
在 和 中,
=
{∠ = ∠ ,
=
∴ ≌ ( ),
∴ = .
20.【答案】【小题1】
第 7 页,共 13 页
解:∵一次函数 = + 1的图像经过点(1,3),
∴ 3 = + 1,
解得 = 2,
∴这个一次函数的解析式为 = 2 + 1;
【小题2】
解:∵点( , 5)在函数 = 2 + 1的图像上,
∴ 5 = 2 + 1,
解得 = 2.
21.【答案】解:∵ ⊥ 于点 ,
∴ ∠ = ∠ = 90 ,
∵ = , = ,
∴ ≌ ( )
∴ ∠ = ∠ ,
∵ ∠ = 90 , ∠ = 40 ,
1
∴ ∠ = × (180 90 40 ) = 25
2
∴ ∠ = 180 90 25 = 65 .
22.【答案】【小题1】
13
√ 13
【小题2】
解:如图,点 表示的数为√ 13.
23.【答案】【小题1】
如图,连接 ,
第 8 页,共 13 页
∵ 的垂直平分线 交 于点 ,
∴ =
∵ =
∴ = ,
∵ 为 中点,
∴ ⊥ ;
【小题2】
∵ = ,∠ = 36
∴ ∠ = ∠ = 36
∴ ∠ = ∠ + ∠ = 72
∵ =
∴ ∠ = ∠ = 72
∴ ∠ = 180 ∠ ∠ = 72 .
24.【答案】【小题1】
解:由题意得, = 2 × 50 + 50 × 0.8( 2) = 40 + 20;
【小题2】
解:在 = 40 + 20中,当 = 200时, = 4.5;
40
200 ÷ (50 × 0.9) = ,
9
40
∵ < 4.5,
9
∴她在老农果园购买更合算.
25.【答案】【小题1】
解: 长是点 到直线 的最短距离;
理由如下:
∵ = √ 5, = 2, = 1,
第 9 页,共 13 页
∴ 2 + 2 = 12 + 22 = 5 = 2,
∴ 是直角三角形,且∠ = 90 ,
即 ⊥ ,
∴ 长是点 到直线 的最短距离;
【小题2】
解:由(1)知, ⊥ ,
5
在 中, = 2, = ,
2
2 2 3由勾股定理得: = √ = ;
2
3
∴点 和点 的距离为 .
2
26.【答案】【小题1】
解:∵ = 2, = 3,
∴ 1 = 2 3, 2 = 3 + 2,
分别令 1 = 0, 2 = 0代入可得:2 3 = 0, 3 + 2 = 0,
3 2
解得: = , = ,
2 3
3 2
∴ 1、 2与 轴的交点坐标分别为( , 0) , ( , 0); 2 3
【小题2】
1
( , 0)
5
【小题3】
解:由函数 1的图像不经过第一象限,可得 < 0, < 0,
把点(1, 4)代入 2 = + 得: + = 4,
∴ = 4 < 0,
∴ 4 < < 0.
27.【答案】【小题1】
解:∵ ′// ,
∴ ∠ = ∠ ′ ,
∵以 为对称轴将 翻折至 ′ ,
第 10 页,共 13 页
∴ ∠ ′ = ∠ ,
∴ ∠ = ∠ ,
∴ 是等腰三角形,
∴ = = 3.
【小题2】
解:如图,以 为对称轴将 翻折至 ′ ,当 ′落在线段 上时,有 ⊥ , = ′,
∴ ∠ = 90 = ∠ ,
又∵ ∠ = ∠ ,
∴ ∽ ,
∴ = ,
又∵ 是直角三角形, = √ 2 + 2 = √ 32 + 42 = 5,
2 32 9
∴ = = = .
5 5
【小题3】
解:如图:
∵以 为对称轴将 翻折至 ′ ,
∴ = ′,∠ = ∠ ′,
∵ ′ ⊥ ,
∴ ∠ = ∠ ′ = 90 ,
∴ ∠ = ∠ ,
又∵ ∠ = ∠ ,
∴ ∽ ,
第 11 页,共 13 页
∴ = ,
2 42 16
∴ = = = ,
5 5
∵在 ′和△ 中,∠ = ∠ ′,∠ ′ = ∠ ,
∴△ ′ ∽△ ,
∴ = ,即 = ,
′ ′
16
5 4
∴ 5 = ,
5
∴解得 = 1.
28.【答案】【小题1】
(1,1)
√ 2
【小题2】
解:如图所示,过点 作 ⊥ 轴交 轴于 ,过点 作 ⊥ 于 ,则 = , = ,
∵ (3,0)、 (0,4),
∴ = = 4, = 3,
∵点 是线段 的“等腰点”,
∴ = ,
∵ ∠ = 90 , ⊥ 轴, ⊥ ,
∴ ∠ = ∠ = ∠ = 90 ,
∴ ∠ + ∠ = ∠ + ∠ = 90 ,
∴ ∠ = ∠ ,
∴ ≌ ( ),
∴ = = , = ,
∴ = + = + = 4, = = = 3,
7
∴ = ,
2
7
∴ = = = ,
2
7 7
∴ ( , );
2 2
第 12 页,共 13 页
【小题3】
解:如图所示,取 中点 ,连接 , ,
∵点 是线段 的“等腰点”,
∴ = ,
∵ ∠ = 60 ,
∴ 是等边三角形;
∵ ( , 0)、 (0, ),
∴ = , = ,
∴ 2 = 2 + 2 = 2 + 2 = 4,
∴ = = 2,
∵ 为 的中点,∠ = 90 ,
1
∴ = = = 1,
2
∴ = √ 2 2 = √ 3,
∵ ≤ + ,
∴当 、 、 三点共线时, 有最大值,最大值为1 + √ 3.
第 13 页,共 13 页
同课章节目录
