17.3.4求一次函数的表达式(含答案)
文档属性
| 名称 | 17.3.4求一次函数的表达式(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-27 16:11:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
17.3.4求一次函数的表达式
一、单选题
1.电话每台月租费元,市区内电话(三分钟以内)每次元,若某台电话每次通话均不超过分钟,则每月应缴费(元)与市内电话通话次数之间的函数关系式是( )
A. B. C. D.
2.直线与x轴的交点是,则k的值是( )
A.3 B.2 C. D.
3.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,以点A为圆心,长为半径画弧,交x轴的负半轴于点C,则直线的解析式为( )
A. B. C. D.
4.过,两点的直线不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法不正确的是( )
A.体育场离林茂家
B.体育场离文具店
C.林茂从体育场出发到文具店的平均速度是
D.林茂从文具店回家的平均速度是
二、填空题
6.若直线y=kx(k≠0)经过点(-2,6),则y随x的增大而
7.已知一次函数的图象经过点A(3,0),与轴交于点B,O为坐标原点. 若△AOB的面积为6,则该一次函数的解析式为 .
8.已知直线l:y=(3-k)x+1经过点(4,9),则它的解析式为 .
9.已知一次函数 ,当x=1时,y=-1,则k= .
10.在平面直角坐标系中,一次函数y=kx+b(k、b为常数,且k≠0)的图象如图所示,根据图象中的信息可求得关于x的方程kx+b=﹣1的解为 .
11.已知直线与平行,且经过点,则 .
三、计算题
12.如图,在平面直角坐标系中,点在直线上,过点的直线交轴于点.求直线的函数表达式.
13.如图,在平面直角坐标系中,点是坐标原点,点,点,其中满足;
(1)求的值;
(2)点从点出发,以每秒2个单位长度的速度沿轴正半轴运动,连接,设点的运动时间为秒,的面积为,用含的式子表示,并直接写出相应的取值范围;
(3)在(2)的条件下,点在上,点在延长线上,,当时,求点的坐标.
四、解答题
14.已知一次函数经过、两点.求这个一次函数的解析式.
五、作图题
15.已知:直线过点(,),且与双曲线:相交于点(,2).
(1)求m值及直线的解析式;
(2)画出的图象,结合图象直接写出不等式的解集.
六、综合题
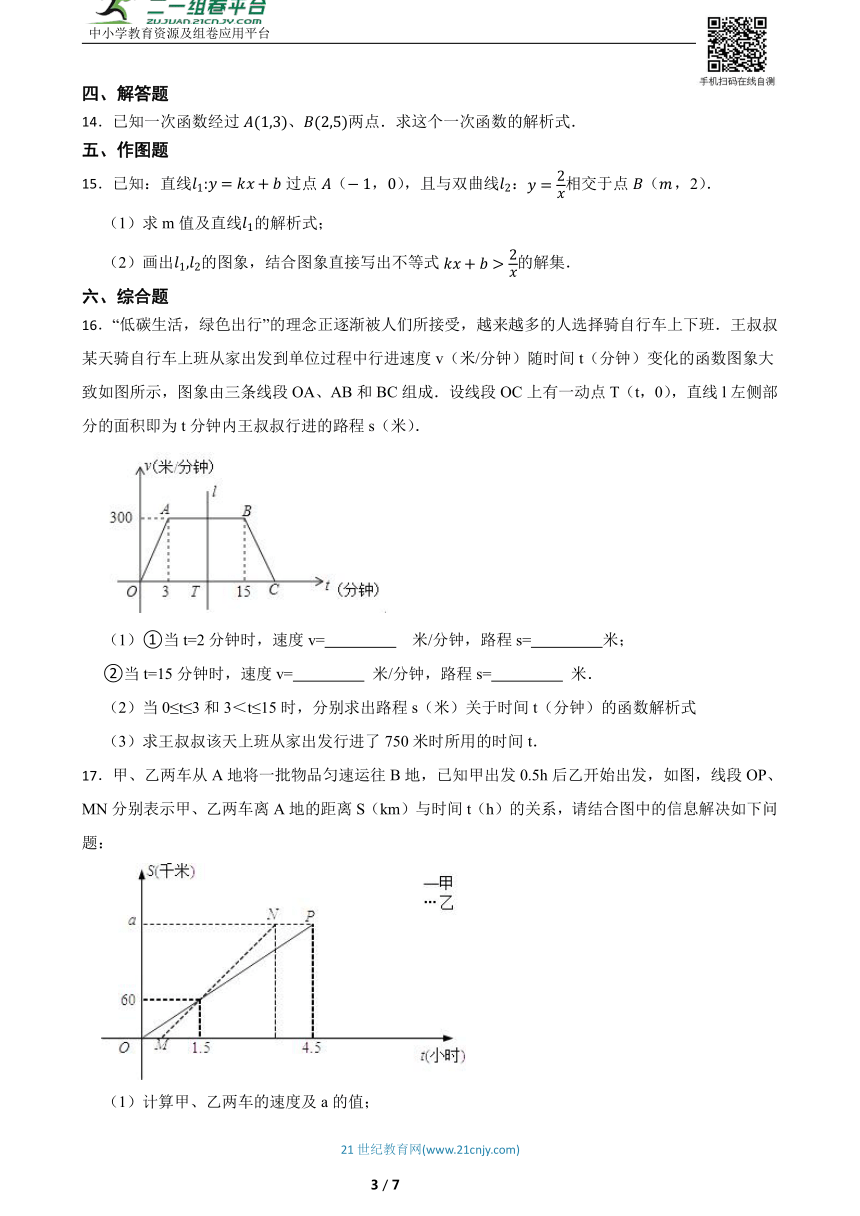
16.“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
(1)①当t=2分钟时,速度v= 米/分钟,路程s= 米;
②当t=15分钟时,速度v= 米/分钟,路程s= 米.
(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式
(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.
17.甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
18.在平面直角坐标系中,直线AB经过(1,1),(-3,5)点;
(1)求直线AB函数表达式;
(2)若点P(a,-2)在直线AB上,求a的值;
七、实践探究题
19.如图,直线与轴、轴分别交于点,.点的坐标为,点的坐标为.
(1)求的值,及一次函数解析式;
(2)若点是第二象限内的直线上的一个动点.当点运动过程中,试写出的面积与的函数关系式,并写出自变量的取值范围;
(3)探究:当运动到什么位置时,的面积为,并说明理由.
答案解析部分
1.【答案】C
【知识点】待定系数法求一次函数解析式
2.【答案】D
【知识点】待定系数法求一次函数解析式
3.【答案】A
【知识点】待定系数法求一次函数解析式;勾股定理;一次函数图象与坐标轴交点问题
4.【答案】B
【知识点】待定系数法求一次函数解析式
5.【答案】C
【知识点】一次函数的实际应用;通过函数图象获取信息
6.【答案】减小
【知识点】正比例函数的图象和性质;待定系数法求一次函数解析式
7.【答案】或
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题
8.【答案】
【知识点】待定系数法求一次函数解析式
9.【答案】1
【知识点】待定系数法求一次函数解析式
10.【答案】x=﹣2.
【知识点】待定系数法求一次函数解析式
11.【答案】10
【知识点】待定系数法求一次函数解析式
12.【答案】直线的解析式为
【知识点】待定系数法求一次函数解析式
13.【答案】(1)
(2)
(3)
【知识点】待定系数法求一次函数解析式;勾股定理
14.【答案】解:设所求的一次函数的解析式为.
把、代入得
,
解得,
所以所求的解析式为.
【知识点】待定系数法求一次函数解析式
15.【答案】(1),;(2)或
【知识点】待定系数法求一次函数解析式
16.【答案】(1)200;200;300;4050
(2)解:①当0≤t≤3,设直线OA的解析式为:v=kt,由图象可知点A(3,300),
∴300=3k,
解得:k=100,
则解析式为:v=100t;
设l与OA的交点为P,则P(t,100t),
∴s=,
②当3<t≤15时,设l与AB的交点为Q,则Q(t,300),
∴S=
(3)解:∵当0≤t≤3,S最大=50×9=450,
∵750>450,
∴当3<t≤15时,450<S≤4050,
则令750=300t﹣450,
解得:t=4.
故王叔叔该天上班从家出发行进了750米时所用的时间4分钟.
【知识点】一次函数的实际应用
17.【答案】(1)解:由题意可知M(0.5,0),线段OP、MN都经过(1.5,60),
甲车的速度60÷1.5=40km/小时,
乙车的速度60÷(1.5﹣0.5)=60km/小时,
a=40×4.5=180km
(2)解:①∵180÷60=3小时,
∴乙车到达B地,所用时间为180÷60=3,所以点N的横坐标为3.5,
6.5小时返回A地,
乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象为线段NQ;
②甲车离A地的距离是:40×3.5=140km;
设乙车返回与甲车相遇所用时间为t0,
则(60+40)t0=180﹣140,
解得t0=0.4h,
60×0.4=24km,
答:甲车在离B地24km处与返程中的乙车相遇.
【知识点】一次函数的实际应用
18.【答案】(1)设直线AB所对应的函数表达式为 (k≠0).
直线AB经过 、 两点,
解得
直线AB所对应的函数表达式为 .
(2) 点 在直线AB上,
.
.
【知识点】待定系数法求一次函数解析式
19.【答案】(1),
(2)
(3),或,
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题
21世纪教育网(www.21cnjy.com)
1 / 7
17.3.4求一次函数的表达式
一、单选题
1.电话每台月租费元,市区内电话(三分钟以内)每次元,若某台电话每次通话均不超过分钟,则每月应缴费(元)与市内电话通话次数之间的函数关系式是( )
A. B. C. D.
2.直线与x轴的交点是,则k的值是( )
A.3 B.2 C. D.
3.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,以点A为圆心,长为半径画弧,交x轴的负半轴于点C,则直线的解析式为( )
A. B. C. D.
4.过,两点的直线不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是:林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家.图中x表示时间,y表示林茂离家的距离.依据图中的信息,下列说法不正确的是( )
A.体育场离林茂家
B.体育场离文具店
C.林茂从体育场出发到文具店的平均速度是
D.林茂从文具店回家的平均速度是
二、填空题
6.若直线y=kx(k≠0)经过点(-2,6),则y随x的增大而
7.已知一次函数的图象经过点A(3,0),与轴交于点B,O为坐标原点. 若△AOB的面积为6,则该一次函数的解析式为 .
8.已知直线l:y=(3-k)x+1经过点(4,9),则它的解析式为 .
9.已知一次函数 ,当x=1时,y=-1,则k= .
10.在平面直角坐标系中,一次函数y=kx+b(k、b为常数,且k≠0)的图象如图所示,根据图象中的信息可求得关于x的方程kx+b=﹣1的解为 .
11.已知直线与平行,且经过点,则 .
三、计算题
12.如图,在平面直角坐标系中,点在直线上,过点的直线交轴于点.求直线的函数表达式.
13.如图,在平面直角坐标系中,点是坐标原点,点,点,其中满足;
(1)求的值;
(2)点从点出发,以每秒2个单位长度的速度沿轴正半轴运动,连接,设点的运动时间为秒,的面积为,用含的式子表示,并直接写出相应的取值范围;
(3)在(2)的条件下,点在上,点在延长线上,,当时,求点的坐标.
四、解答题
14.已知一次函数经过、两点.求这个一次函数的解析式.
五、作图题
15.已知:直线过点(,),且与双曲线:相交于点(,2).
(1)求m值及直线的解析式;
(2)画出的图象,结合图象直接写出不等式的解集.
六、综合题
16.“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班.王叔叔某天骑自行车上班从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
(1)①当t=2分钟时,速度v= 米/分钟,路程s= 米;
②当t=15分钟时,速度v= 米/分钟,路程s= 米.
(2)当0≤t≤3和3<t≤15时,分别求出路程s(米)关于时间t(分钟)的函数解析式
(3)求王叔叔该天上班从家出发行进了750米时所用的时间t.
17.甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
18.在平面直角坐标系中,直线AB经过(1,1),(-3,5)点;
(1)求直线AB函数表达式;
(2)若点P(a,-2)在直线AB上,求a的值;
七、实践探究题
19.如图,直线与轴、轴分别交于点,.点的坐标为,点的坐标为.
(1)求的值,及一次函数解析式;
(2)若点是第二象限内的直线上的一个动点.当点运动过程中,试写出的面积与的函数关系式,并写出自变量的取值范围;
(3)探究:当运动到什么位置时,的面积为,并说明理由.
答案解析部分
1.【答案】C
【知识点】待定系数法求一次函数解析式
2.【答案】D
【知识点】待定系数法求一次函数解析式
3.【答案】A
【知识点】待定系数法求一次函数解析式;勾股定理;一次函数图象与坐标轴交点问题
4.【答案】B
【知识点】待定系数法求一次函数解析式
5.【答案】C
【知识点】一次函数的实际应用;通过函数图象获取信息
6.【答案】减小
【知识点】正比例函数的图象和性质;待定系数法求一次函数解析式
7.【答案】或
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题
8.【答案】
【知识点】待定系数法求一次函数解析式
9.【答案】1
【知识点】待定系数法求一次函数解析式
10.【答案】x=﹣2.
【知识点】待定系数法求一次函数解析式
11.【答案】10
【知识点】待定系数法求一次函数解析式
12.【答案】直线的解析式为
【知识点】待定系数法求一次函数解析式
13.【答案】(1)
(2)
(3)
【知识点】待定系数法求一次函数解析式;勾股定理
14.【答案】解:设所求的一次函数的解析式为.
把、代入得
,
解得,
所以所求的解析式为.
【知识点】待定系数法求一次函数解析式
15.【答案】(1),;(2)或
【知识点】待定系数法求一次函数解析式
16.【答案】(1)200;200;300;4050
(2)解:①当0≤t≤3,设直线OA的解析式为:v=kt,由图象可知点A(3,300),
∴300=3k,
解得:k=100,
则解析式为:v=100t;
设l与OA的交点为P,则P(t,100t),
∴s=,
②当3<t≤15时,设l与AB的交点为Q,则Q(t,300),
∴S=
(3)解:∵当0≤t≤3,S最大=50×9=450,
∵750>450,
∴当3<t≤15时,450<S≤4050,
则令750=300t﹣450,
解得:t=4.
故王叔叔该天上班从家出发行进了750米时所用的时间4分钟.
【知识点】一次函数的实际应用
17.【答案】(1)解:由题意可知M(0.5,0),线段OP、MN都经过(1.5,60),
甲车的速度60÷1.5=40km/小时,
乙车的速度60÷(1.5﹣0.5)=60km/小时,
a=40×4.5=180km
(2)解:①∵180÷60=3小时,
∴乙车到达B地,所用时间为180÷60=3,所以点N的横坐标为3.5,
6.5小时返回A地,
乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象为线段NQ;
②甲车离A地的距离是:40×3.5=140km;
设乙车返回与甲车相遇所用时间为t0,
则(60+40)t0=180﹣140,
解得t0=0.4h,
60×0.4=24km,
答:甲车在离B地24km处与返程中的乙车相遇.
【知识点】一次函数的实际应用
18.【答案】(1)设直线AB所对应的函数表达式为 (k≠0).
直线AB经过 、 两点,
解得
直线AB所对应的函数表达式为 .
(2) 点 在直线AB上,
.
.
【知识点】待定系数法求一次函数解析式
19.【答案】(1),
(2)
(3),或,
【知识点】待定系数法求一次函数解析式;一次函数图象与坐标轴交点问题
21世纪教育网(www.21cnjy.com)
1 / 7
