人教版数学九下 27.2 相似三角形 课时训练(含答案)
文档属性
| 名称 | 人教版数学九下 27.2 相似三角形 课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 378.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-28 08:46:20 | ||
图片预览


文档简介
人教版数学中考第二十七章第二节《相似三角形》课时训练
一、选择题
1.如图,,且,,则的长为( )
A.6 B.9 C.3 D.4
2.如图,D、E分别是的边、上的点,下列各比例式不一定能推得的是( )
A. B. C. D.
3.如图,在和中,,要使与相似,还需要添加一个条件,这个条件是( )
A. B. C. D.
4.如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是 ( )
A.S1=S3 B.S2=2S1
C.S2=2S4 D.S1S3=S2S4
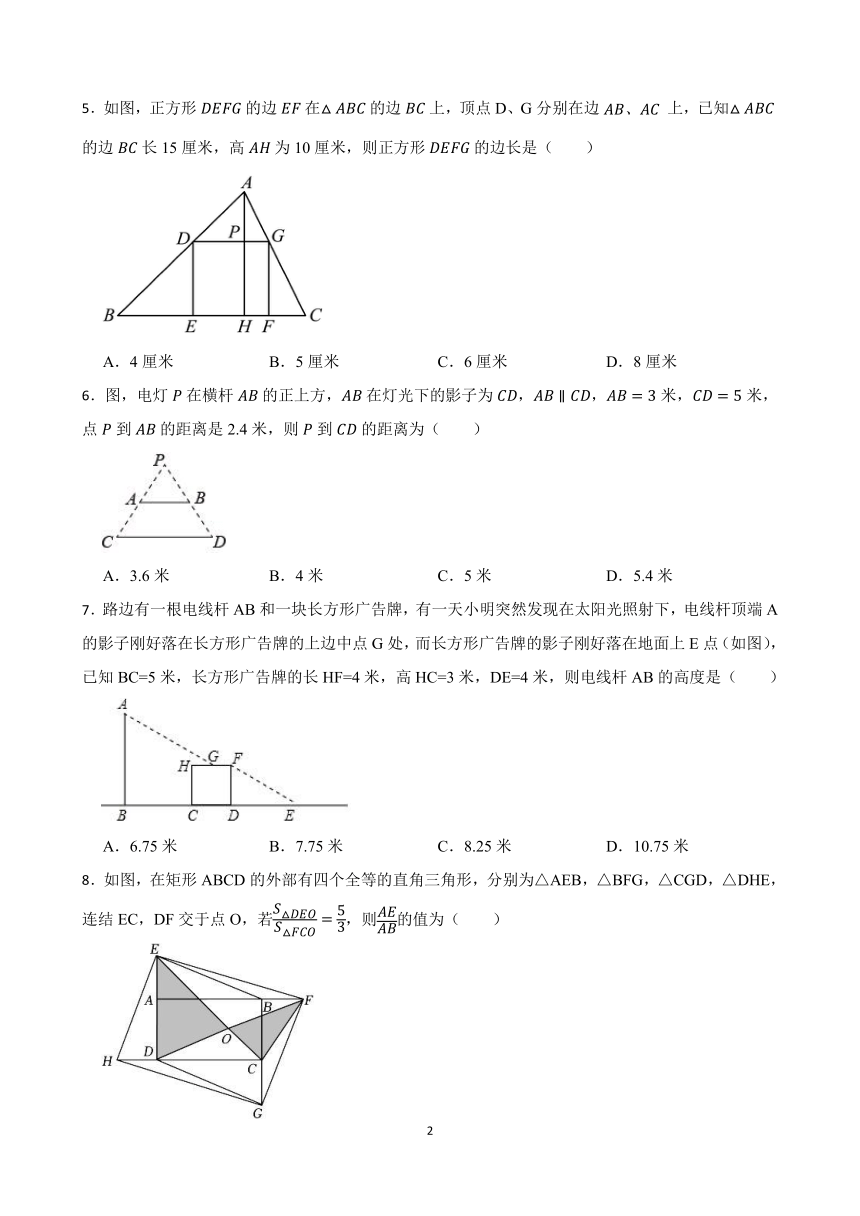
5.如图,正方形的边在的边上,顶点D、G分别在边 上,已知的边长15厘米,高为10厘米,则正方形的边长是( )
A.4厘米 B.5厘米 C.6厘米 D.8厘米
6.图,电灯在横杆的正上方,在灯光下的影子为,,米,米,点到的距离是2.4米,则到的距离为( )
A.3.6米 B.4米 C.5米 D.5.4米
7.路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( )
A.6.75米 B.7.75米 C.8.25米 D.10.75米
8.如图,在矩形ABCD的外部有四个全等的直角三角形,分别为△AEB,△BFG,△CGD,△DHE,连结EC,DF交于点O,若,则的值为( )
A. B. C. D.
二、填空题
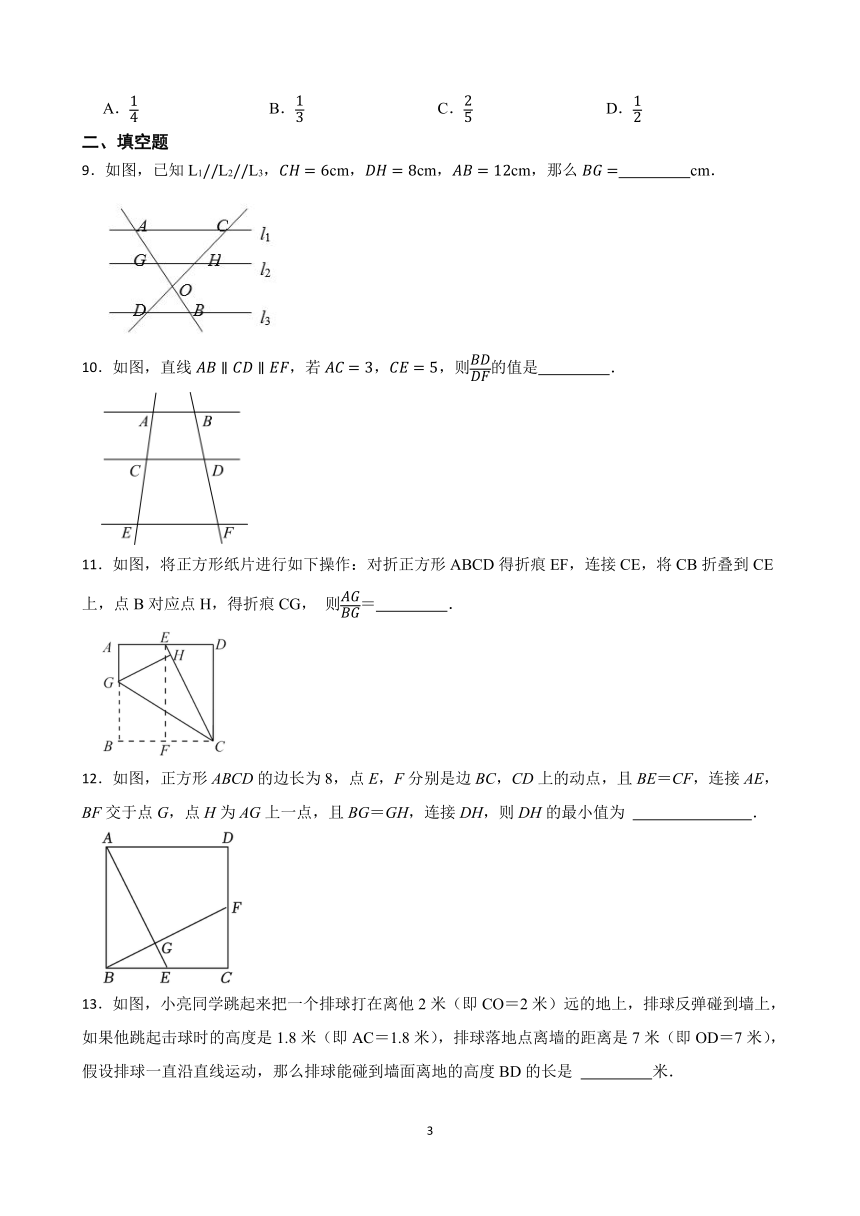
9.如图,已知L1L2L3,cm,cm,cm,那么 cm.
10.如图,直线,若,,则的值是 .
11.如图,将正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B对应点H,得折痕CG, 则= .
12.如图,正方形ABCD的边长为8,点E,F分别是边BC,CD上的动点,且BE=CF,连接AE,BF交于点G,点H为AG上一点,且BG=GH,连接DH,则DH的最小值为 .
13.如图,小亮同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是7米(即OD=7米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
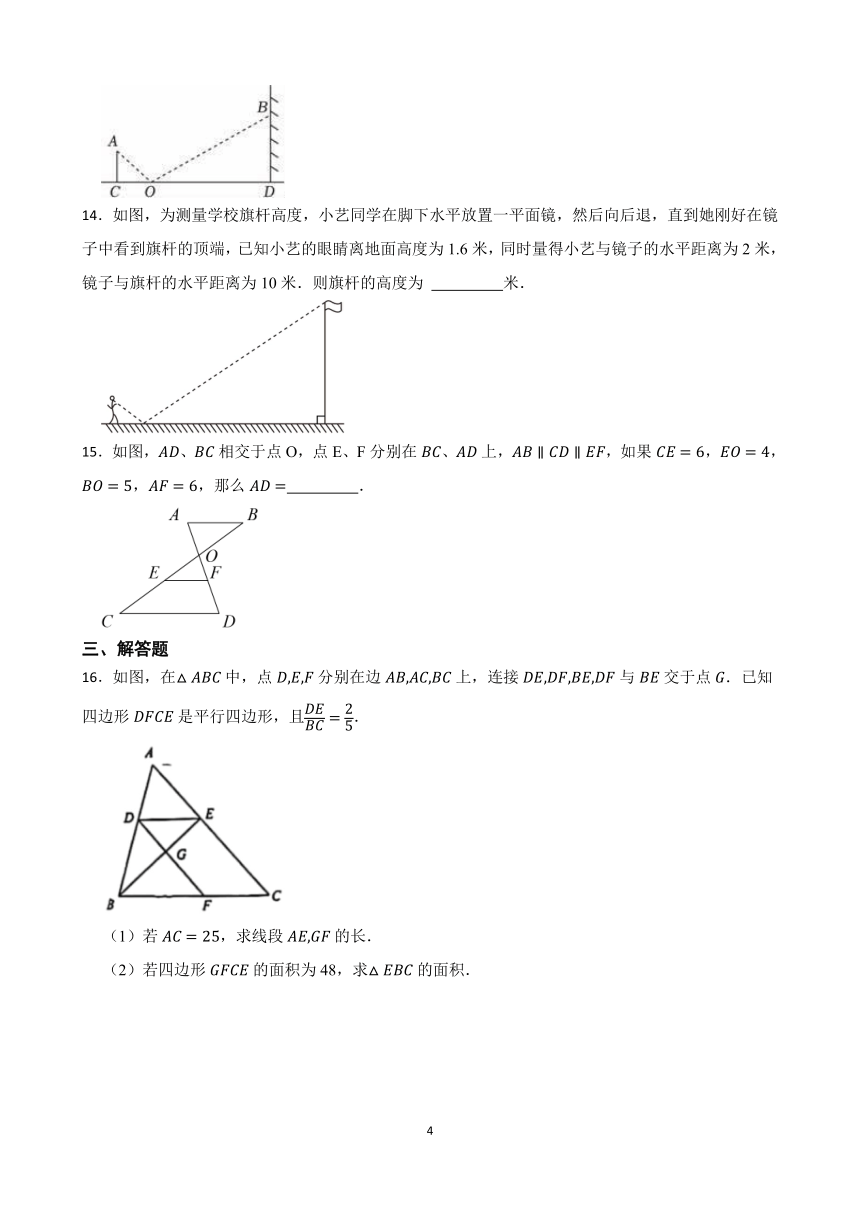
14.如图,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退,直到她刚好在镜子中看到旗杆的顶端,已知小艺的眼睛离地面高度为1.6米,同时量得小艺与镜子的水平距离为2米,镜子与旗杆的水平距离为10米.则旗杆的高度为 米.
15.如图,、相交于点O,点E、F分别在、上,,如果,,,,那么 .
三、解答题
16.如图,在中,点分别在边上,连接与交于点.已知四边形是平行四边形,且.
(1)若,求线段的长.
(2)若四边形的面积为48,求的面积.
17.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
18.如图,在中,点E在上,,和相交于点F,过点F作,交于点G.
(1)求的值.
(2)若,
①求证:.
②求证:.
19.如图,抛物线与x轴交于A、B两点,与y轴交于点C,直线过B、C两点,连接AC.
(1)求抛物线的解析式;
(2)求证:△AOC∽△ACB;
(3)抛物线对称轴上是否存在点P使得PC+PA的最小值?若存在,求出点P坐标;若不存在,请说明理由.
20.【基础巩固】
(1)如图1,在中,是的中点,是的一个三等分点,且.连结,交于点,则_________;_________.
【尝试应用】
(2)如图2,在中,为上一点,,,若,,,求的长.
【拓展提高】
(3)如图3,在中,为上一点,为中点,与,分别交于点,,若,,,,求的长.
21.如图,在Rt△ABC中,∠ACB=90°,AC=2,D是BC边上一点,连接AD,CD=1,AD=BD,点E,F分别在AD、BD上,EF∥AB,连接CE.
(1)求AB的长;
(2)如图1,若5DE-5AE=3,过点F作FG∥DA,交AB于点G,求S四边形AEFG:S△DEF的值;
(3)如图2,若EF=时,过点F作FH⊥CE,垂足为H,求HF的长.
22.已知:如图,在中,,点由点出发沿方向向点匀速运动,速度为;点由点出发沿方向向点匀速运动,速度为:若设运动的时间为,解答下列问题:
图① 图② 图③
(1)如图①,连接,当为何值时,并说明理由;
(2)如图②,当点运动时,是否存在某一时刻,使得点在线段的垂直平分线上,请说明理由;
(3)如图③,当点运动时,线段上是否存在一点,使得四边形为荾形?若存在,试求出长:若不存在,请说明理由.
23.某数学兴趣小组在数学课外活动中,对四边形做了如下探究.
(1)如图1,在正方形中,点、分别是、上的两点,连接、,,则的值为______.
(2)如图2,在矩形中,,,点、分别是、上的两点,连接、,,求的值.
(3)如图3,在四边形中,,为上一点,连接,过点作的垂线交的延长线于点,交的延长线于点,且,,.求的长.
24.我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.
(1)请在图中画出路灯O和影子端点Q的位置.
(2)估计路灯的高,并求影长的步数.
(3)无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得,,,小明眼睛到地面的距离为,则树高为 m.
25.如图,抛物线与轴交于,两点(点在点的左侧),与轴交于点,点是抛物线上异于点的一个动点,直线与直线交于点.
(1)求直线的函数解析式;
(2)在点运动的过程中,当时,求的面积;;
(3)当点在第一象限抛物线上运动时,连接,设的面积为,的面积为,求的最大值及此时点的坐标.
答案
1-8 ACBCC BCA
9.
10.
11.
12.4﹣4
13.6.3
14.8
15.10
16.(1)解:∵四边形是平行四边形,
∴ DE∥BC,DE=FC
∴△ADE∽△ABC
∴
∴
∴AE=10,CE=15
∵FG∥CE
∴△BFG∽△BCE
∴
∵
∴
∴
∴FG=9.
(2)解:由(1)知: △BFG∽△BCE,
∴
∴
∴
∴S△BFG=27
∴S△EBC=S△BFG+S四边形GFCE=27+48=75.
17.(1)证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)解:∵tan∠ABD=1,∠ADB=90°
∴ =1,
∴AD=BD,
∵△ACD∽△BFD,
∴ = =1,
∴BF=AC=3.
18.(1)解:因为在中,,,
又∵,
∴,
∴,
(2)解:①证明:∵,
可设,则,
由(1)知:,
∴,
∴,,
∴,
又∵,
∴,
∴;
②证明:∵,
∴,
又∵,
∴,
∴,
又∵,
∴,
∴,
∴.
19.(1)解:∵直线y=-x+2过B、C两点,
当x=0时,代入y=-x+2,得y=2,
即C(0,2),
当y=0时,代入y=-x+2,得x=4,
即B(4,0),
把B(4,0),C(0,2)分别代入y=-x2+bx+c,得,
解得:,
∴抛物线的解析式为y=-x2+x+2;
(2)证明:∵抛物线y=-x2+x+2与x轴交于点A,
则y=-x2+x+2=0,
解得x1=-1,x2=4,
∴点A的坐标为(-1,0),
∴AO=1,AB=5,
在Rt△AOC中,AO=1,OC=2,
∴AC=,
∴,
而,
又∵∠OAC=∠CAB,
∴△AOC∽△ACB;
(3)解:存在,理由:
点A关于抛物线对称轴的对称点为点B,则AC和抛物线对称轴的交点即为点P,
理由:PA+PC=PB+PC=BC为最小,
由点B、C的坐标得,直线BC的表达式为:y=-x+2,
当x=时,y=-x+2=-+2=,
即点P(,).
20.(1);;(2);(3)
21.(1)AB的长为;
(2)S四边形AEFG:S△DEF=4:3;
(3)HF的长为.
22.(1)解:在中,,,
由运动知,,,
,,,;
(2)解:存在,
理由:如图②,
由运动知,,,
点在的垂直平分线上,过点作,
,
,,,,.
(3)解:不存在,
理由:由运动知,,
假设线段上是存在一点,使得四边形为平行四边形,
,,,,
,,,
平行四边形不可能是菱形.
即:线段上不存在一点,使得四边形为菱形.
23.(1)
(2)
(3)
24.(1)解:路灯O和影子端点Q的位置如图所示.
(2)解:∵,
∴,
∴,即,
解得.
∵,
∴,
∴,即,
解得,
∴路灯的高为,影长为步.
(3)9
25.(1)
(2)的面积为2.5或7.5
(3)的最大值为,此时,点D
一、选择题
1.如图,,且,,则的长为( )
A.6 B.9 C.3 D.4
2.如图,D、E分别是的边、上的点,下列各比例式不一定能推得的是( )
A. B. C. D.
3.如图,在和中,,要使与相似,还需要添加一个条件,这个条件是( )
A. B. C. D.
4.如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是 ( )
A.S1=S3 B.S2=2S1
C.S2=2S4 D.S1S3=S2S4
5.如图,正方形的边在的边上,顶点D、G分别在边 上,已知的边长15厘米,高为10厘米,则正方形的边长是( )
A.4厘米 B.5厘米 C.6厘米 D.8厘米
6.图,电灯在横杆的正上方,在灯光下的影子为,,米,米,点到的距离是2.4米,则到的距离为( )
A.3.6米 B.4米 C.5米 D.5.4米
7.路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( )
A.6.75米 B.7.75米 C.8.25米 D.10.75米
8.如图,在矩形ABCD的外部有四个全等的直角三角形,分别为△AEB,△BFG,△CGD,△DHE,连结EC,DF交于点O,若,则的值为( )
A. B. C. D.
二、填空题
9.如图,已知L1L2L3,cm,cm,cm,那么 cm.
10.如图,直线,若,,则的值是 .
11.如图,将正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B对应点H,得折痕CG, 则= .
12.如图,正方形ABCD的边长为8,点E,F分别是边BC,CD上的动点,且BE=CF,连接AE,BF交于点G,点H为AG上一点,且BG=GH,连接DH,则DH的最小值为 .
13.如图,小亮同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是7米(即OD=7米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是 米.
14.如图,为测量学校旗杆高度,小艺同学在脚下水平放置一平面镜,然后向后退,直到她刚好在镜子中看到旗杆的顶端,已知小艺的眼睛离地面高度为1.6米,同时量得小艺与镜子的水平距离为2米,镜子与旗杆的水平距离为10米.则旗杆的高度为 米.
15.如图,、相交于点O,点E、F分别在、上,,如果,,,,那么 .
三、解答题
16.如图,在中,点分别在边上,连接与交于点.已知四边形是平行四边形,且.
(1)若,求线段的长.
(2)若四边形的面积为48,求的面积.
17.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
18.如图,在中,点E在上,,和相交于点F,过点F作,交于点G.
(1)求的值.
(2)若,
①求证:.
②求证:.
19.如图,抛物线与x轴交于A、B两点,与y轴交于点C,直线过B、C两点,连接AC.
(1)求抛物线的解析式;
(2)求证:△AOC∽△ACB;
(3)抛物线对称轴上是否存在点P使得PC+PA的最小值?若存在,求出点P坐标;若不存在,请说明理由.
20.【基础巩固】
(1)如图1,在中,是的中点,是的一个三等分点,且.连结,交于点,则_________;_________.
【尝试应用】
(2)如图2,在中,为上一点,,,若,,,求的长.
【拓展提高】
(3)如图3,在中,为上一点,为中点,与,分别交于点,,若,,,,求的长.
21.如图,在Rt△ABC中,∠ACB=90°,AC=2,D是BC边上一点,连接AD,CD=1,AD=BD,点E,F分别在AD、BD上,EF∥AB,连接CE.
(1)求AB的长;
(2)如图1,若5DE-5AE=3,过点F作FG∥DA,交AB于点G,求S四边形AEFG:S△DEF的值;
(3)如图2,若EF=时,过点F作FH⊥CE,垂足为H,求HF的长.
22.已知:如图,在中,,点由点出发沿方向向点匀速运动,速度为;点由点出发沿方向向点匀速运动,速度为:若设运动的时间为,解答下列问题:
图① 图② 图③
(1)如图①,连接,当为何值时,并说明理由;
(2)如图②,当点运动时,是否存在某一时刻,使得点在线段的垂直平分线上,请说明理由;
(3)如图③,当点运动时,线段上是否存在一点,使得四边形为荾形?若存在,试求出长:若不存在,请说明理由.
23.某数学兴趣小组在数学课外活动中,对四边形做了如下探究.
(1)如图1,在正方形中,点、分别是、上的两点,连接、,,则的值为______.
(2)如图2,在矩形中,,,点、分别是、上的两点,连接、,,求的值.
(3)如图3,在四边形中,,为上一点,连接,过点作的垂线交的延长线于点,交的延长线于点,且,,.求的长.
24.我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.
(1)请在图中画出路灯O和影子端点Q的位置.
(2)估计路灯的高,并求影长的步数.
(3)无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得,,,小明眼睛到地面的距离为,则树高为 m.
25.如图,抛物线与轴交于,两点(点在点的左侧),与轴交于点,点是抛物线上异于点的一个动点,直线与直线交于点.
(1)求直线的函数解析式;
(2)在点运动的过程中,当时,求的面积;;
(3)当点在第一象限抛物线上运动时,连接,设的面积为,的面积为,求的最大值及此时点的坐标.
答案
1-8 ACBCC BCA
9.
10.
11.
12.4﹣4
13.6.3
14.8
15.10
16.(1)解:∵四边形是平行四边形,
∴ DE∥BC,DE=FC
∴△ADE∽△ABC
∴
∴
∴AE=10,CE=15
∵FG∥CE
∴△BFG∽△BCE
∴
∵
∴
∴
∴FG=9.
(2)解:由(1)知: △BFG∽△BCE,
∴
∴
∴
∴S△BFG=27
∴S△EBC=S△BFG+S四边形GFCE=27+48=75.
17.(1)证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)解:∵tan∠ABD=1,∠ADB=90°
∴ =1,
∴AD=BD,
∵△ACD∽△BFD,
∴ = =1,
∴BF=AC=3.
18.(1)解:因为在中,,,
又∵,
∴,
∴,
(2)解:①证明:∵,
可设,则,
由(1)知:,
∴,
∴,,
∴,
又∵,
∴,
∴;
②证明:∵,
∴,
又∵,
∴,
∴,
又∵,
∴,
∴,
∴.
19.(1)解:∵直线y=-x+2过B、C两点,
当x=0时,代入y=-x+2,得y=2,
即C(0,2),
当y=0时,代入y=-x+2,得x=4,
即B(4,0),
把B(4,0),C(0,2)分别代入y=-x2+bx+c,得,
解得:,
∴抛物线的解析式为y=-x2+x+2;
(2)证明:∵抛物线y=-x2+x+2与x轴交于点A,
则y=-x2+x+2=0,
解得x1=-1,x2=4,
∴点A的坐标为(-1,0),
∴AO=1,AB=5,
在Rt△AOC中,AO=1,OC=2,
∴AC=,
∴,
而,
又∵∠OAC=∠CAB,
∴△AOC∽△ACB;
(3)解:存在,理由:
点A关于抛物线对称轴的对称点为点B,则AC和抛物线对称轴的交点即为点P,
理由:PA+PC=PB+PC=BC为最小,
由点B、C的坐标得,直线BC的表达式为:y=-x+2,
当x=时,y=-x+2=-+2=,
即点P(,).
20.(1);;(2);(3)
21.(1)AB的长为;
(2)S四边形AEFG:S△DEF=4:3;
(3)HF的长为.
22.(1)解:在中,,,
由运动知,,,
,,,;
(2)解:存在,
理由:如图②,
由运动知,,,
点在的垂直平分线上,过点作,
,
,,,,.
(3)解:不存在,
理由:由运动知,,
假设线段上是存在一点,使得四边形为平行四边形,
,,,,
,,,
平行四边形不可能是菱形.
即:线段上不存在一点,使得四边形为菱形.
23.(1)
(2)
(3)
24.(1)解:路灯O和影子端点Q的位置如图所示.
(2)解:∵,
∴,
∴,即,
解得.
∵,
∴,
∴,即,
解得,
∴路灯的高为,影长为步.
(3)9
25.(1)
(2)的面积为2.5或7.5
(3)的最大值为,此时,点D
