2024-2025学年上海位育中学高二上学期数学期末试卷(2025.01)(含答案)
文档属性
| 名称 | 2024-2025学年上海位育中学高二上学期数学期末试卷(2025.01)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 865.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-28 08:10:23 | ||
图片预览




文档简介
位育中学2024学年第一学期高二年级数学期末
2025.01
一、填空题(本大题共有12题,第1-6题每题3分,第7-12题每题4分,满分42分)
1.用数学符号表示“直线在平面上”为________.
2.“抛掷一枚骰子,观察朝上的点数”的样本空间为________.
3.若圆锥的母线为,高为1,则圆锥的侧面积为________.
4.已知向量,,若,则实数的值为________.
5.半径为3的球的体积为________.
6.若样本数据,,…,的方差为16,则数据,,的标准差为________.
7.设,是两个相互独立事件,且,,则________.
8.有7个同学要排队做操,其中甲乙丙必须相邻,则总共有________种排法.
9.在直三棱柱中,,,,,则点到平面的距离为________
10.袋子中有红、黄、黑、白共四个小球,有放回地从中任取一个小球,直到红、黄两个小球都取到才停止,用随机模拟的方法估计恰好抽取三次停止的概率.用1,2,3,4分别代表红、黄、黑、白四个小球,利用电脑随机产生1到4之间取整数值的随机数,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
341 332 341 144 221 132 243 331 112
342 241 244 342 142 431 233 214 344
由此可以估计,恰好抽取三次就停止的概率为________.
11.在平行六面体中,,且,则________.
12.正三棱锥中,底面边长,侧棱,空间向量,满足,,则的最大值为________.
二、选择题(本大题共有4题,每题4分,满分16分)
13、下列命题正确的是( )
A.如果一个平面内有无数条直线与另一个平面平行,则这两个平面平行
B.如果两个平面垂直于同一个平面,那么这两个平面平行
C.如果一条直线与平面内的一条直线平行,则该直线与此平面平行
D.如果两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直
14.在四棱锥中,若,则实数组可能是( )
A. B. C. D.
15.一个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.经过重复摸球足够多次试验后发现,摸到黑球的频率稳定在0.1左右,则据此估计盒子中红球的个数约为( )
A.40个 B.45个 C.50个 D.55个
16.,分别为菱形的边,的中点,将菱形沿对角线折起,使点不在平面内,则在翻折过程中,对于下列两个命题:①直线恒与平面平行;②异面直线与恒垂直.以下判断正确的是( )
A.①为真命题,②为真命题 B.①为真命题,②为假命题
C.①为假命题,②为真命题 D.①为假命题,②为假命题
三、解答题(本大题共有5题,满分42分)
17.(本题满分6分)
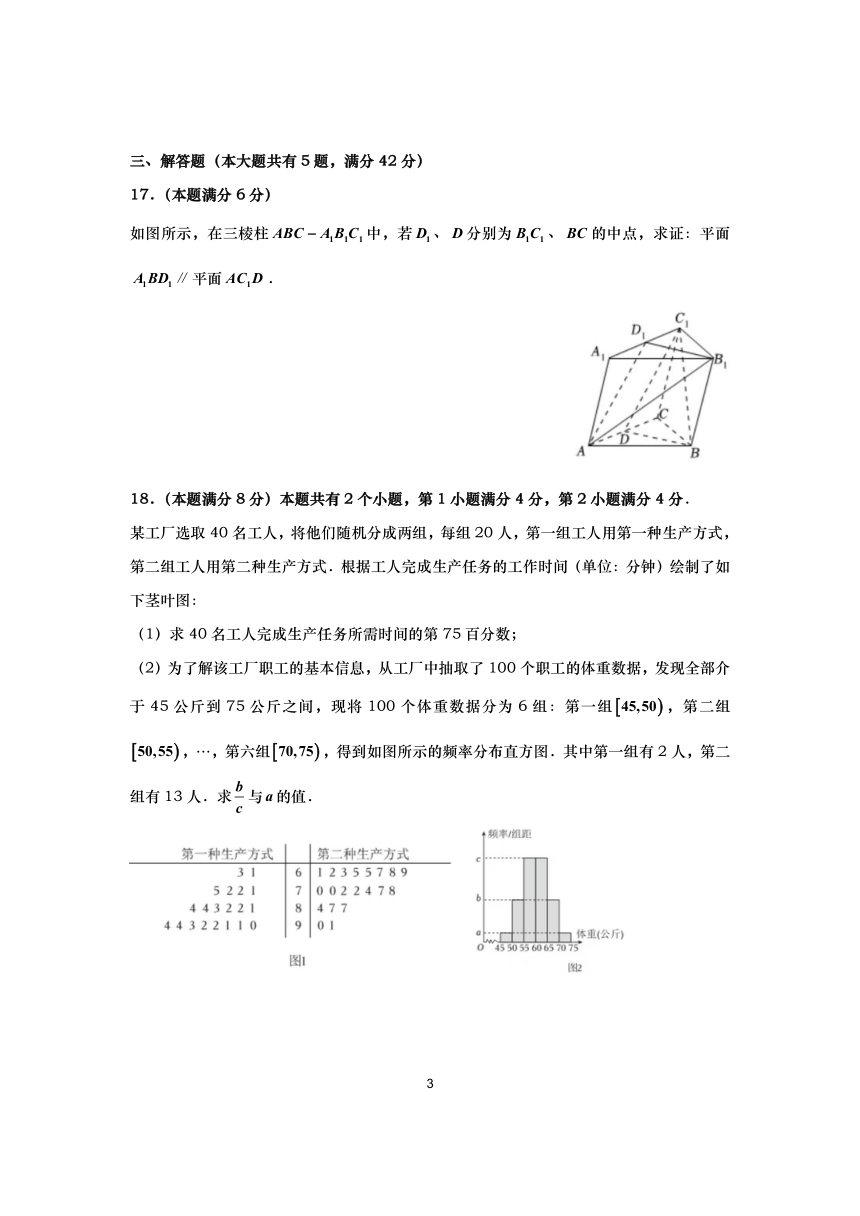
如图所示,在三棱柱中,若、分别为、的中点,求证:平面平面.
18.(本题满分8分)本题共有2个小题,第1小题满分4分,第2小题满分4分.
某工厂选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:分钟)绘制了如下茎叶图:
(1)求40名工人完成生产任务所需时间的第75百分数;
(2)为了解该工厂职工的基本信息,从工厂中抽取了100个职工的体重数据,发现全部介于45公斤到75公斤之间,现将100个体重数据分为6组:第一组,第二组,…,第六组,得到如图所示的频率分布直方图.其中第一组有2人,第二组有13人.求与的值.
19.(本题满分9分)本题共有2小题,第1小题满分4分,第2小题满分5分.
甲、乙两人都是围棋爱好者,某天两人要进行一场比赛,甲每局比赛获胜的概率是0.7(每局比赛仅有胜利或者失败两种可能),且每局之间的胜负互不影响,最终胜者将赢得100元的奖金.比赛开始后不久,就因为有其他要事而中止了比赛.
(I)若是三局两胜的比赛(谁先胜两局比赛立即结束),且甲已经获胜一局后中止了比赛,则甲最终获胜的概率为多少
(2)若是五局三胜的比赛(谁先胜三局比赛立即结束),在已知甲、乙各胜1局的情况下中止了比赛,如何分配奖金比较公平
20.(本题满分9分)本题共有2小题,第1小题满分4分,第2小题满分5分.
如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为,高为,杯内有深的溶液。现将水杯倾斜,且倾斜时点始终在桌面上。在倾斜过程中一直保持溶液不会溢出,且设直径所在直线与桌面所成的角为(图②).
(1)求图②圆柱的母线与液面所在平面所成的角(用表示);
(2)要使倾斜后容器内的溶液不会溢出,求角的最大值.
21.(本题满分10分)本题共有2个小题,第1小题满分4分,第2小题满分6分.
如图,在三棱锥中,侧面,是全等的直角三角形,是公共的斜边,且,,另一个侧面是正三角形.
(1)求证:;
(2)求二面角的大小;
参考答案
一、填空题
1.; 2.点朝上点朝上点朝上点朝上),点朝上点朝上; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.;
11.; 12.;
11.在平行六面体中,,
且,则________.
【答案】
【解析】因为
所以
所以.故答案为:
12.正三棱锥中,底面边长,侧棱,空间向量,满足,,则的最大值为________
【答案】4
【解析】由三棱锥是正三棱锥,可得,且,由化简得,根据化简得.
设,代入,,分别化简得且,
因此,点在以为直径的球面上,半径
在以为直径的球面上,半径分别取线段的中点,
则,故,故答案为:4.
二、选择题
13.D; 14.B; 15.B; 16.A
15.个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.经过重复摸球足够多次试验后发现,摸到黑球的频率稳定在0.1左右,则据此估计盒子中红球的个数约为( )
A.40个 B.45个 C.50个 D.55个
【答案】
【解析】设盒子中球的总数为,由题意可知,,解得,
所以估计盒子中红球的个数约为个.故答案为:.
16.,分别为菱形的边,的中点,将菱形沿对角线折起,使点不在平面内,则在翻折过程中,对于下列两个命题:①直线恒与平面平行;②异面直线与恒垂直.以下判断正确的是( )
A.①为真命题,②为真命题 B.①为真命题,②为假命题
C.①为假命题,②为真命题 D.①为假命题,②为假命题
【答案】
【解析】对于①:由于分别为菱形的边,的中点,
所以,由于平面平面,故直线恒与平面平行;
故①正确;对于②,取的中点,连接和,如图所示:
根据菱形的性质,所以,
故平面;由于平面,所以,
由于,所以,故②正确.故选:.
三、解答题
17.证明略
18.(1) (2)
19.(1)0.91 (2)甲分配奖金78.4元,乙分配奖金21.6元
20.如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为,高为,杯内有深的溶液。现将水杯倾斜,且倾斜时点始终在桌面上。在倾斜过程中一直保持溶液不会溢出,且设直径所在直线与桌面所成的角为(图②).
(1)求图②圆柱的母线与液面所在平面所成的角(用表示);
(2)要使倾斜后容器内的溶液不会溢出,求角的最大值.
【答案】(1) (2)
【解析】(1)如图,过点作,交于,过点作,交延长线于点,过点作,交于,则,
∴图②中圆锥的母线与液面所在平面所成的角为:
图②圆柱的母线与液面所在平面所成的角为;
(2)根据题意,画出图形,如图所示,过作,交所在的直线于,
在直角中,,,
且点在线段上,,此时容器内能容纳的溶液量为:
而容器内原有溶液量为
令,解得
所以,即的最大角为时,溶液不会溢出
21.如图,在三棱锥中,侧面,是全等的直角三角形,是公共的斜边,且,,另一个侧面是正三角形.
(1)求证:;
(2)求二面角的大小;
【答案】(1)见解析 (2)
【解析】(1)作面于,连.,又,,
∴,
又,则是正方形,则.
(2)作于,作交于,
则就是二面角的平面角,
因为,
∵是的中点,则,,,
由余弦定理可求得,∴二面角的余弦值为.
2025.01
一、填空题(本大题共有12题,第1-6题每题3分,第7-12题每题4分,满分42分)
1.用数学符号表示“直线在平面上”为________.
2.“抛掷一枚骰子,观察朝上的点数”的样本空间为________.
3.若圆锥的母线为,高为1,则圆锥的侧面积为________.
4.已知向量,,若,则实数的值为________.
5.半径为3的球的体积为________.
6.若样本数据,,…,的方差为16,则数据,,的标准差为________.
7.设,是两个相互独立事件,且,,则________.
8.有7个同学要排队做操,其中甲乙丙必须相邻,则总共有________种排法.
9.在直三棱柱中,,,,,则点到平面的距离为________
10.袋子中有红、黄、黑、白共四个小球,有放回地从中任取一个小球,直到红、黄两个小球都取到才停止,用随机模拟的方法估计恰好抽取三次停止的概率.用1,2,3,4分别代表红、黄、黑、白四个小球,利用电脑随机产生1到4之间取整数值的随机数,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
341 332 341 144 221 132 243 331 112
342 241 244 342 142 431 233 214 344
由此可以估计,恰好抽取三次就停止的概率为________.
11.在平行六面体中,,且,则________.
12.正三棱锥中,底面边长,侧棱,空间向量,满足,,则的最大值为________.
二、选择题(本大题共有4题,每题4分,满分16分)
13、下列命题正确的是( )
A.如果一个平面内有无数条直线与另一个平面平行,则这两个平面平行
B.如果两个平面垂直于同一个平面,那么这两个平面平行
C.如果一条直线与平面内的一条直线平行,则该直线与此平面平行
D.如果两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直
14.在四棱锥中,若,则实数组可能是( )
A. B. C. D.
15.一个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.经过重复摸球足够多次试验后发现,摸到黑球的频率稳定在0.1左右,则据此估计盒子中红球的个数约为( )
A.40个 B.45个 C.50个 D.55个
16.,分别为菱形的边,的中点,将菱形沿对角线折起,使点不在平面内,则在翻折过程中,对于下列两个命题:①直线恒与平面平行;②异面直线与恒垂直.以下判断正确的是( )
A.①为真命题,②为真命题 B.①为真命题,②为假命题
C.①为假命题,②为真命题 D.①为假命题,②为假命题
三、解答题(本大题共有5题,满分42分)
17.(本题满分6分)
如图所示,在三棱柱中,若、分别为、的中点,求证:平面平面.
18.(本题满分8分)本题共有2个小题,第1小题满分4分,第2小题满分4分.
某工厂选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:分钟)绘制了如下茎叶图:
(1)求40名工人完成生产任务所需时间的第75百分数;
(2)为了解该工厂职工的基本信息,从工厂中抽取了100个职工的体重数据,发现全部介于45公斤到75公斤之间,现将100个体重数据分为6组:第一组,第二组,…,第六组,得到如图所示的频率分布直方图.其中第一组有2人,第二组有13人.求与的值.
19.(本题满分9分)本题共有2小题,第1小题满分4分,第2小题满分5分.
甲、乙两人都是围棋爱好者,某天两人要进行一场比赛,甲每局比赛获胜的概率是0.7(每局比赛仅有胜利或者失败两种可能),且每局之间的胜负互不影响,最终胜者将赢得100元的奖金.比赛开始后不久,就因为有其他要事而中止了比赛.
(I)若是三局两胜的比赛(谁先胜两局比赛立即结束),且甲已经获胜一局后中止了比赛,则甲最终获胜的概率为多少
(2)若是五局三胜的比赛(谁先胜三局比赛立即结束),在已知甲、乙各胜1局的情况下中止了比赛,如何分配奖金比较公平
20.(本题满分9分)本题共有2小题,第1小题满分4分,第2小题满分5分.
如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为,高为,杯内有深的溶液。现将水杯倾斜,且倾斜时点始终在桌面上。在倾斜过程中一直保持溶液不会溢出,且设直径所在直线与桌面所成的角为(图②).
(1)求图②圆柱的母线与液面所在平面所成的角(用表示);
(2)要使倾斜后容器内的溶液不会溢出,求角的最大值.
21.(本题满分10分)本题共有2个小题,第1小题满分4分,第2小题满分6分.
如图,在三棱锥中,侧面,是全等的直角三角形,是公共的斜边,且,,另一个侧面是正三角形.
(1)求证:;
(2)求二面角的大小;
参考答案
一、填空题
1.; 2.点朝上点朝上点朝上点朝上),点朝上点朝上; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.;
11.; 12.;
11.在平行六面体中,,
且,则________.
【答案】
【解析】因为
所以
所以.故答案为:
12.正三棱锥中,底面边长,侧棱,空间向量,满足,,则的最大值为________
【答案】4
【解析】由三棱锥是正三棱锥,可得,且,由化简得,根据化简得.
设,代入,,分别化简得且,
因此,点在以为直径的球面上,半径
在以为直径的球面上,半径分别取线段的中点,
则,故,故答案为:4.
二、选择题
13.D; 14.B; 15.B; 16.A
15.个不透明的盒子中装有若干个红球和5个黑球,这些球除颜色外均相同.每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子.经过重复摸球足够多次试验后发现,摸到黑球的频率稳定在0.1左右,则据此估计盒子中红球的个数约为( )
A.40个 B.45个 C.50个 D.55个
【答案】
【解析】设盒子中球的总数为,由题意可知,,解得,
所以估计盒子中红球的个数约为个.故答案为:.
16.,分别为菱形的边,的中点,将菱形沿对角线折起,使点不在平面内,则在翻折过程中,对于下列两个命题:①直线恒与平面平行;②异面直线与恒垂直.以下判断正确的是( )
A.①为真命题,②为真命题 B.①为真命题,②为假命题
C.①为假命题,②为真命题 D.①为假命题,②为假命题
【答案】
【解析】对于①:由于分别为菱形的边,的中点,
所以,由于平面平面,故直线恒与平面平行;
故①正确;对于②,取的中点,连接和,如图所示:
根据菱形的性质,所以,
故平面;由于平面,所以,
由于,所以,故②正确.故选:.
三、解答题
17.证明略
18.(1) (2)
19.(1)0.91 (2)甲分配奖金78.4元,乙分配奖金21.6元
20.如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为,高为,杯内有深的溶液。现将水杯倾斜,且倾斜时点始终在桌面上。在倾斜过程中一直保持溶液不会溢出,且设直径所在直线与桌面所成的角为(图②).
(1)求图②圆柱的母线与液面所在平面所成的角(用表示);
(2)要使倾斜后容器内的溶液不会溢出,求角的最大值.
【答案】(1) (2)
【解析】(1)如图,过点作,交于,过点作,交延长线于点,过点作,交于,则,
∴图②中圆锥的母线与液面所在平面所成的角为:
图②圆柱的母线与液面所在平面所成的角为;
(2)根据题意,画出图形,如图所示,过作,交所在的直线于,
在直角中,,,
且点在线段上,,此时容器内能容纳的溶液量为:
而容器内原有溶液量为
令,解得
所以,即的最大角为时,溶液不会溢出
21.如图,在三棱锥中,侧面,是全等的直角三角形,是公共的斜边,且,,另一个侧面是正三角形.
(1)求证:;
(2)求二面角的大小;
【答案】(1)见解析 (2)
【解析】(1)作面于,连.,又,,
∴,
又,则是正方形,则.
(2)作于,作交于,
则就是二面角的平面角,
因为,
∵是的中点,则,,,
由余弦定理可求得,∴二面角的余弦值为.
同课章节目录
