18.2平行四边形的判定(含答案)
文档属性
| 名称 | 18.2平行四边形的判定(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 248.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-28 17:52:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
18.2平行四边形的判定
一、单选题
1.如图,在四边形中,AB∥CD,添加下列一个条件后,一定能判定四边形是平行四边形的是( )
A. B. C. D.
2.如图,对四边形 ABCD 增加条件,使之成为平行四边形,下面添加不正确的是( )
A. B.
C. D. 与 相互平分
3.在四边形中,对角线相交于点O,下列条件不能判断四边形是平行四边形的是( )
A. B.
C. D.
4. 已知四边形,以下有四组条件:① ;②;③;④,其中能判四边形是平行四边形的条件共有( )
A.1组 B.2组 C.3组 D.1组
5.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm,点D是AC上一点,以AD,BD为邻边作平行四边形ADBE ,则对角线DE的最小值是( )
A.4 B.6 C.8 D.10
二、填空题
6.在中,点E,F分别在边BC,AD上,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形AECF是平行四边形.
7.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成了一个四边形ABCD,当线段AD=13时,线段BC的长为 .
8.阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图1,及边的中点,求作:平行四边形.
小静的作法如下:
在数学课上,老师提出如下问题:
①连接并延长,在延长线上截取;
②连接.所以四边形就是所求作的平行四边形.
老师说:“小静的作法正确”.
请回答:小静的作法正确的理由是 .
9.如图,在中,点,在对角线上,添加一个适当的条件,使四边形是平行四边形,这个条件可以是 .(填一个条件即可,不添加任何辅助线)
10.如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕,小宇测得长边,则四边形的周长为 .
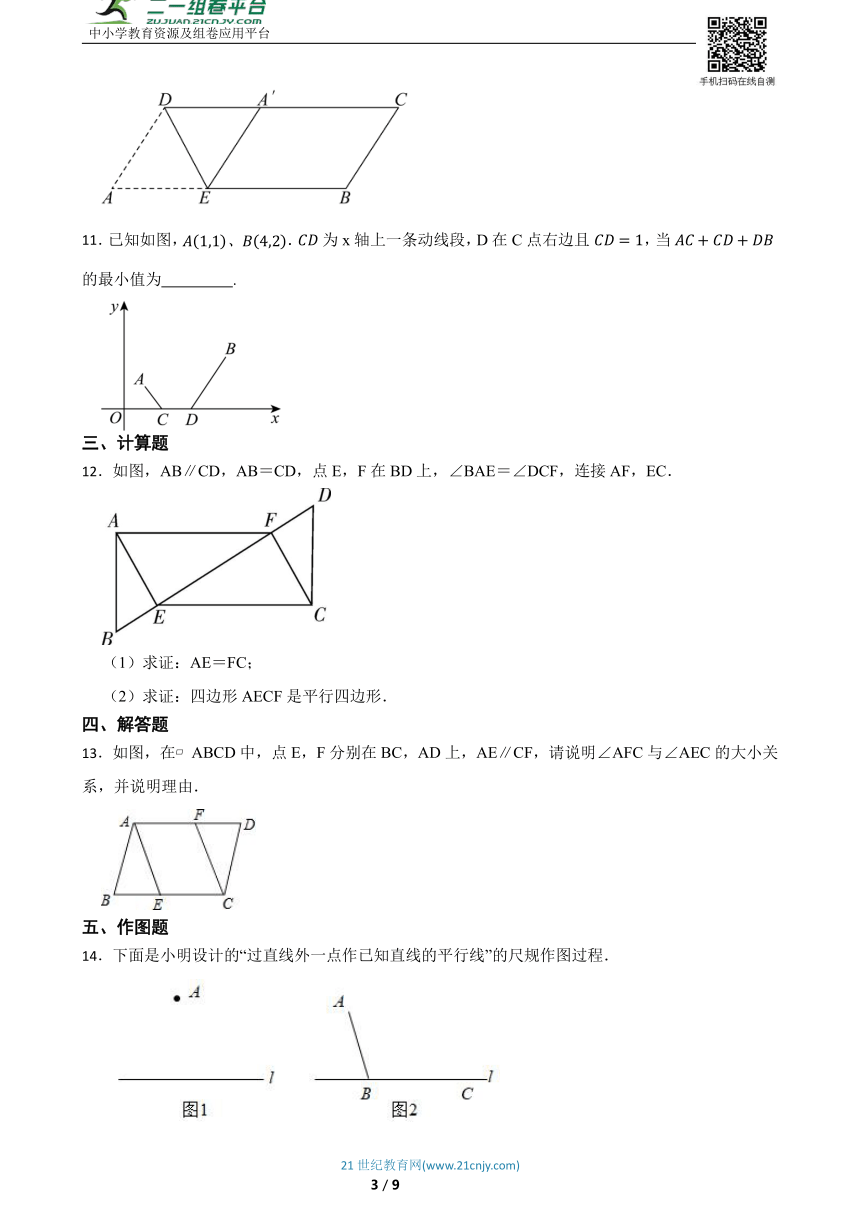
11.已知如图,.为x轴上一条动线段,D在C点右边且,当的最小值为 .
三、计算题
12.如图,AB∥CD,AB=CD,点E,F在BD上,∠BAE=∠DCF,连接AF,EC.
(1)求证:AE=FC;
(2)求证:四边形AECF是平行四边形.
四、解答题
13.如图,在 ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说明理由.
五、作图题
14.下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:如图1,直线l 及直线l 外一点A.
求作:直线AD,使得AD// l.
作法:如图2,
①在直线l 上任取两点B,C,连接AB;
②分别以点A,C 为圆心,线段BC,AB 长为半径画弧,两弧在直线l 上方相交于点D;
③作直线AD.
直线AD 就是所求作的直线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接CD.
∵ AB =▲,BC =▲,
∴ 四边形ABCD 为平行四边形( )(填推理的依据).
∴ AD// l.
六、综合题
15.
(1)如图,以线段、为邻边,用尺规作图画出平行四边形保留作图痕迹,并说明它用了平行四边形的哪个判定方法?
(2)连接、,若,,,求平行四边形的面积.
16.如图,在梯形ABCD中,AB∥CD.
(1)已知∠A=∠B,求证:AD=BC;
(2)已知AD=BC,求证:∠A=∠B.
17.如图,四边形ABCD中, 于点E, 于点F, , .求证:
(1) ;
(2)四边形ABCD是平行四边形.
答案解析部分
1.【答案】C
【知识点】平行四边形的判定
2.【答案】B
【知识点】平行四边形的判定
3.【答案】A
【知识点】平行四边形的判定
4.【答案】A
【知识点】平行四边形的判定
5.【答案】B
【知识点】垂线段最短及其应用;勾股定理;平行四边形的判定与性质
6.【答案】(答案不唯一)
【知识点】平行四边形的性质;平行四边形的判定
7.【答案】13
【知识点】平行四边形的判定与性质
8.【答案】对角线互相平分的四边形是平行四边形
【知识点】平行四边形的判定
9.【答案】答案不唯一,如或
【知识点】平行四边形的判定
10.【答案】
【知识点】平行四边形的性质;平行四边形的判定;翻折变换(折叠问题)
11.【答案】
【知识点】两点之间线段最短;勾股定理;平行四边形的判定与性质
12.【答案】(1)证明:(1)∵AB∥CD,
∴∠B=∠D.
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),
∴AE=FC.
(2)解:由(1)△ABE≌△CDF,得AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,即∠AEF=∠CFE,
∴AE∥CF.
∵AE=CF,
∴四边形AECF是平行四边形.
【知识点】平行线的判定与性质;平行四边形的判定;三角形全等的判定-ASA
13.【答案】解:∠AFC=∠AEC,
理由如下:∵平行四边形ABCD中,BC∥AD,
又AE∥CF,
∴四边形AECF为平行四边形,
∴∠AEC=∠AFC
【知识点】平行四边形的判定与性质
14.【答案】(1)解:如图所示,
(2)证明:连接CD.
∵ AB =CD,BC =AD,
∴ 四边形ABCD 为平行四边形(两组对边分别相等的四边形是平行四边形)(填推理的依据).
∴ AD// l.
故答案为:,,两组对边分别相等的四边形是平行四边形.
【知识点】平行四边形的判定与性质;作图-平行线
15.【答案】(1)解:如图:
结论:两组对边分别相等的四边形是平行四边形.
(2)解:如图:
设AC和BD交于点O,
四边形ABCD是平行四边形,
,,
,,
,,
,
,
,
,
.
【知识点】平行四边形的判定
16.【答案】(1)解:如图,过点C作CE∥DA,交AB于点E
∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵CE∥DA
∴∠A=∠CEB
又∵∠A=∠B
∴∠CEB=∠B
∴EC=BC
∴AD=BC
(2)解:∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵AD=BC
∴EC=BC
∴∠CEB=∠B
又∵CE∥DA
∴∠CEB=∠A
∴∠B=∠A
【知识点】等式的基本性质;等腰三角形的性质;平行四边形的判定与性质
17.【答案】(1)解:∵ ,
∴∠AEB=∠CFD=90°
又∵ ,
∴ (SAS)
(2)解:∵
∴∠ABE=∠CDF,AB=CD,
∴AB∥CD
∴四边形ABCD是平行四边形
【知识点】平行四边形的判定;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 9
18.2平行四边形的判定
一、单选题
1.如图,在四边形中,AB∥CD,添加下列一个条件后,一定能判定四边形是平行四边形的是( )
A. B. C. D.
2.如图,对四边形 ABCD 增加条件,使之成为平行四边形,下面添加不正确的是( )
A. B.
C. D. 与 相互平分
3.在四边形中,对角线相交于点O,下列条件不能判断四边形是平行四边形的是( )
A. B.
C. D.
4. 已知四边形,以下有四组条件:① ;②;③;④,其中能判四边形是平行四边形的条件共有( )
A.1组 B.2组 C.3组 D.1组
5.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm,点D是AC上一点,以AD,BD为邻边作平行四边形ADBE ,则对角线DE的最小值是( )
A.4 B.6 C.8 D.10
二、填空题
6.在中,点E,F分别在边BC,AD上,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形AECF是平行四边形.
7.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成了一个四边形ABCD,当线段AD=13时,线段BC的长为 .
8.阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图1,及边的中点,求作:平行四边形.
小静的作法如下:
在数学课上,老师提出如下问题:
①连接并延长,在延长线上截取;
②连接.所以四边形就是所求作的平行四边形.
老师说:“小静的作法正确”.
请回答:小静的作法正确的理由是 .
9.如图,在中,点,在对角线上,添加一个适当的条件,使四边形是平行四边形,这个条件可以是 .(填一个条件即可,不添加任何辅助线)
10.如图,小宇将一张平行四边形纸片折叠,使点落在长边上的点处,并得到折痕,小宇测得长边,则四边形的周长为 .
11.已知如图,.为x轴上一条动线段,D在C点右边且,当的最小值为 .
三、计算题
12.如图,AB∥CD,AB=CD,点E,F在BD上,∠BAE=∠DCF,连接AF,EC.
(1)求证:AE=FC;
(2)求证:四边形AECF是平行四边形.
四、解答题
13.如图,在 ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说明理由.
五、作图题
14.下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:如图1,直线l 及直线l 外一点A.
求作:直线AD,使得AD// l.
作法:如图2,
①在直线l 上任取两点B,C,连接AB;
②分别以点A,C 为圆心,线段BC,AB 长为半径画弧,两弧在直线l 上方相交于点D;
③作直线AD.
直线AD 就是所求作的直线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接CD.
∵ AB =▲,BC =▲,
∴ 四边形ABCD 为平行四边形( )(填推理的依据).
∴ AD// l.
六、综合题
15.
(1)如图,以线段、为邻边,用尺规作图画出平行四边形保留作图痕迹,并说明它用了平行四边形的哪个判定方法?
(2)连接、,若,,,求平行四边形的面积.
16.如图,在梯形ABCD中,AB∥CD.
(1)已知∠A=∠B,求证:AD=BC;
(2)已知AD=BC,求证:∠A=∠B.
17.如图,四边形ABCD中, 于点E, 于点F, , .求证:
(1) ;
(2)四边形ABCD是平行四边形.
答案解析部分
1.【答案】C
【知识点】平行四边形的判定
2.【答案】B
【知识点】平行四边形的判定
3.【答案】A
【知识点】平行四边形的判定
4.【答案】A
【知识点】平行四边形的判定
5.【答案】B
【知识点】垂线段最短及其应用;勾股定理;平行四边形的判定与性质
6.【答案】(答案不唯一)
【知识点】平行四边形的性质;平行四边形的判定
7.【答案】13
【知识点】平行四边形的判定与性质
8.【答案】对角线互相平分的四边形是平行四边形
【知识点】平行四边形的判定
9.【答案】答案不唯一,如或
【知识点】平行四边形的判定
10.【答案】
【知识点】平行四边形的性质;平行四边形的判定;翻折变换(折叠问题)
11.【答案】
【知识点】两点之间线段最短;勾股定理;平行四边形的判定与性质
12.【答案】(1)证明:(1)∵AB∥CD,
∴∠B=∠D.
在△ABE和△CDF中,
∴△ABE≌△CDF(ASA),
∴AE=FC.
(2)解:由(1)△ABE≌△CDF,得AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,即∠AEF=∠CFE,
∴AE∥CF.
∵AE=CF,
∴四边形AECF是平行四边形.
【知识点】平行线的判定与性质;平行四边形的判定;三角形全等的判定-ASA
13.【答案】解:∠AFC=∠AEC,
理由如下:∵平行四边形ABCD中,BC∥AD,
又AE∥CF,
∴四边形AECF为平行四边形,
∴∠AEC=∠AFC
【知识点】平行四边形的判定与性质
14.【答案】(1)解:如图所示,
(2)证明:连接CD.
∵ AB =CD,BC =AD,
∴ 四边形ABCD 为平行四边形(两组对边分别相等的四边形是平行四边形)(填推理的依据).
∴ AD// l.
故答案为:,,两组对边分别相等的四边形是平行四边形.
【知识点】平行四边形的判定与性质;作图-平行线
15.【答案】(1)解:如图:
结论:两组对边分别相等的四边形是平行四边形.
(2)解:如图:
设AC和BD交于点O,
四边形ABCD是平行四边形,
,,
,,
,,
,
,
,
,
.
【知识点】平行四边形的判定
16.【答案】(1)解:如图,过点C作CE∥DA,交AB于点E
∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵CE∥DA
∴∠A=∠CEB
又∵∠A=∠B
∴∠CEB=∠B
∴EC=BC
∴AD=BC
(2)解:∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵AD=BC
∴EC=BC
∴∠CEB=∠B
又∵CE∥DA
∴∠CEB=∠A
∴∠B=∠A
【知识点】等式的基本性质;等腰三角形的性质;平行四边形的判定与性质
17.【答案】(1)解:∵ ,
∴∠AEB=∠CFD=90°
又∵ ,
∴ (SAS)
(2)解:∵
∴∠ABE=∠CDF,AB=CD,
∴AB∥CD
∴四边形ABCD是平行四边形
【知识点】平行四边形的判定;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
2 / 9
