第18章平行四边形(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第18章平行四边形
一、单选题
1.如图,在平行四边形ABCD中,∠A:∠B=7:2,则∠A的度数是( )
A.110° B.140° C.120° D.160°
2.如图,E,F,G,H分别为四边形边的中点,要使四边形为矩形,应添加的条件是( )
A. B. C. D.
3.我们已经学过两种全等变换:平移和轴对称,通过变换可以把两条分散的线段拼接在一起.请借助变换解决下面问题:如图,四边形中,,,,则的最小值为( )
A.4 B.6 C. D.
4.如图,在平面直角坐标系中的位置如所示,顶点,,点B在x轴正半轴上,以点O为圆心,以小于长为半径作弧,分别交边,于点D,E,分别以点D,E为圆心,以大于长为半径作弧,两弧在内交于点F,作射线,交边于点G,则点G的坐标为( )
A. B. C. D.
5.在平行四边形中,,则的度数为( )
A. B. C. D.
6.如图,平行四边形的对角线AC,BD交于点O,已知BC=6,BD=12,AC=8,则△OAD的周长为( )
A.13 B.14 C.16 D.18
7.如图,平行四边形ABCD的对角线相交于点O,AO=4,OD=7,△DBC的周长比△ABC的周长( )
A.长6 B.短6 C.短3 D.长3
8.在中,对角线与交于点,在延长线上取一点,连接交于.已知,,,则的长等于( )
A. B. C. D.
9.如图,在 ABCD中,∠B是锐角,点F是AB边的中点,AE⊥BC于点E,连接DF,EF.若∠EFD=90°,AD=2,AB=,则AE长为( )
A.2 B. C. D.
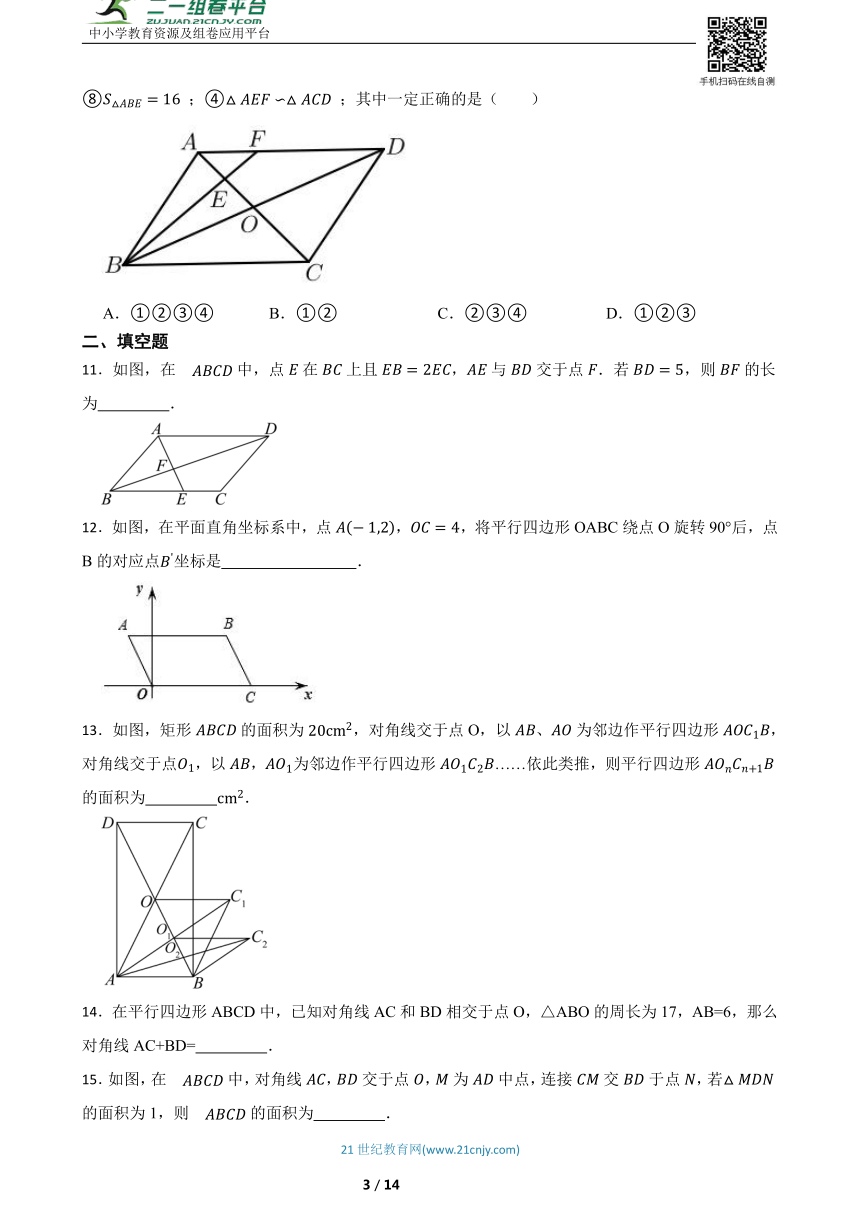
10.如图,平行四边形 中, 、 相交于点 ,点 是 的中点,连接 并延长交 于点 , ,则下列 结论:① ;② ;⑧ ;④ ;其中一定正确的是( )
A.①②③④ B.①② C.②③④ D.①②③
二、填空题
11.如图,在中,点在上且,与交于点.若,则的长为 .
12.如图,在平面直角坐标系中,点,,将平行四边形OABC绕点O旋转90°后,点B的对应点坐标是 .
13.如图,矩形的面积为,对角线交于点O,以、为邻边作平行四边形,对角线交于点,以,为邻边作平行四边形……依此类推,则平行四边形的面积为 .
14.在平行四边形ABCD中,已知对角线AC和BD相交于点O,△ABO的周长为17,AB=6,那么对角线AC+BD= .
15.如图,在中,对角线,交于点,为中点,连接交于点,若的面积为1,则的面积为 .
16.如图,等边中,,为中点,,为边上的动点,且,则的最小值是 .
三、计算题
17.如图,一次函数与反比例函数的图象在第一象限的交点横坐标为1,直线轴于点,且与一次函数和反比例函数的图象分别交于点和点,且点在点上方.
(1)求反比例函数的表达式;
(2)若四边形是平行四边形,求的值.
18.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
19.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,满足,直线经过轴负半轴上的点,且.
(1)求直线的函数表达式;
(2)平移直线,平移后的直线与直线交于点,与轴交于点.
①已知平面内有一点,连接,当的值最小时,求的值;
②若平移后的直线与轴交于点,是否存在点,使以点为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
四、解答题
20.如图,在四边形中,,,,,点P从点D出发,以每秒1个单位长度的速度向点A运动,点Q从点B同时出发,以每秒2个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P运动时间为t秒.
(1)当点P运动停止时,______,线段的长为______;
(2)①用含t的式子填空:______,______,______;
② t为何值时,四边形为矩形,求出t的值;
(3)在运动的过程中,是否存在某一时刻t,使以P,D,C,Q为顶点的四边形为平行四边形?若存在,请求出t的值,若不存在,请说明理由.
21.如图,在 ABCD中,E、F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形,并证明.
22.如图,AM是的中线,是线段AM上一点(不与点A重合),DE//AB,交AC于点,交DF于点,连结AE.
(1)如图①,当点D与点M重合时,求证:四边形ABDE是平行四边形.
(2)如图②,当点D不与点M重合时,(1)中的结论还成立吗?请说明理由.
23.如图,在直角梯形 ABCD中,AB∥CD,∠BCD =90°,AB=AD=10cm,BC=8cm.点 P从点A 出发,以每秒 3c m的速度沿折线 ABCD 向点 D 运动,点 Q 从点 D 出发,以每秒 2cm 的速度沿线段 DC 向点 C 运动.已知动点 P,Q 同时出发,当点 Q运动到点C 时,P,Q两点同时停止运动,设运动时间为 t(s).
(1)求 CD的长.
(2)当四边形 PBQD 为平行四边形时,求四边形PBQD 的周长.
(3)在运动过程中,是否存在某一时刻,使得△BPQ的面积为 20 cm 若存在,请求出所有满足条件的 t的值;若不存在,请说明理由.
答案解析部分
1.【答案】C
【知识点】平行四边形的性质
2.【答案】D
【知识点】平行四边形的判定与性质;矩形的判定;三角形的中位线定理
3.【答案】D
【知识点】勾股定理;平行四边形的判定与性质
4.【答案】A
【知识点】坐标与图形性质;平行四边形的性质;尺规作图-作角的平分线;坐标系中的两点距离公式
5.【答案】B
【知识点】平行四边形的性质
6.【答案】C
【知识点】平行四边形的性质
7.【答案】A
【知识点】平行四边形的性质
8.【答案】B
【知识点】平行四边形的性质;相似三角形的判定与性质;三角形的中位线定理
9.【答案】B
【知识点】线段垂直平分线的性质;勾股定理;平行四边形的性质;三角形全等的判定-AAS
10.【答案】B
【知识点】平行四边形的性质;相似三角形的判定与性质;四边形的综合
11.【答案】
【知识点】平行四边形的性质;相似三角形的判定与性质
12.【答案】或
【知识点】平行四边形的性质;旋转的性质;坐标与图形变化﹣旋转
13.【答案】
【知识点】平行四边形的性质;矩形的性质;中心对称及中心对称图形
14.【答案】22
【知识点】平行四边形的性质
15.【答案】12
【知识点】平行四边形的性质;相似三角形的判定与性质
16.【答案】
【知识点】平行四边形的判定与性质;三角形的中位线定理
17.【答案】(1)
(2)
【知识点】反比例函数与一次函数的交点问题;平行四边形的性质
18.【答案】解:∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形,
∴CD=AB=2,
∴S梯形OBCD==;
∴图中阴影部分的面积=S梯形OBCD-S扇形OBD=-×π×12=-。
【知识点】平行四边形的性质;平行四边形的判定;扇形面积的计算
19.【答案】(1)解:∵,
而,,
∴,,
解得:,,
∴,,
∴,
∵,,
∴,
∴,
∴,
设直线的函数表达式为,
将点,代入表达式可得:
可得,
解得:,
∴直线的函数表达式为.
(2)解:①根据题意,平移直线,平移后的直线与直线交于点,与轴交于点,∴可设直线的函数表达式为;
设直线的函数表达式为,
将点,代入,
可得,
解得:,
∴直线的函数表达式为:;
如下图,连接,
∵,
∴当点在同一直线上时,取最小值,
此时,设直线的解析式为,
将点,代入MC的解析式得:
可得,
解得:,
∴直线的解析式为,
联立解方程组,
得:,
∴,
∴将点代入直线表达式,
可得,
解得:;
②(Ⅰ)当点在点右侧时,如下图,过点作轴于点,
∵四边形为平行四边形,
∴,,
∴,
在△AOC和△EMD中,
∴,
∴,即,
将代入直线的表达式,
可得,解得,
∴,
∴将点代入直线表达式,
可得,解得,即;
(Ⅱ)当点在点左侧时,如下图,过点作轴于点,
∵四边形为平行四边形,
∴,,
∴,
在△AOC和△E ND 中,
∴,
∴,即,
将代入直线的表达式,
可得,解得,
∴,
∴将点代入直线表达式,
可得,解得,即.
综上可得,点的坐标为或.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题;平行四边形的性质;一次函数中的动态几何问题;一次函数图象的平移变换
20.【答案】(1);
(2)①;;;②
(3)
【知识点】平行四边形的性质;矩形的判定;一元一次方程的实际应用-几何问题
21.【答案】解:△ADF≌△CBE,
理由:∵四边形ABCD是平行四边形,
∴AD=BC,∠DAC=∠BCA,
∵BE∥DF,
∴∠DFC=∠BEA,
∴∠AFD=∠BEC,
在△ADF与CBE中,
,
∴△ADF≌△CBE(AAS).
【知识点】平行线的性质;平行四边形的性质;三角形全等的判定-AAS
22.【答案】(1)证明:如图1,∵AM是△ABC的中线,D与M重合,
∴DC=BD,
∵DE∥AB,
∴∠EDC=∠B,
∵CE∥AM,即CE∥AD,
∴∠ECD=∠ADB,
在△ECD和△ADB中,,
∴△ECD≌△ADB(ASA),
∴DE=AB,
∴四边形ABDE是平行四边形;
(2)解:(1)中的结论成立,
理由:如图2,过点M作MG∥AB交CE于点G,
∵DE∥AB,
∴MG∥DE,
∵CE∥AM,
∴四边形DEGM是平行四边形,
∴MG=DE,
同(1)得MG=AB,
∴DE=AB,
∴四边形ABDE是平行四边形.
【知识点】平行四边形的判定与性质;三角形全等的判定-ASA
23.【答案】(1)解:过点A作AM⊥CD于M,
∵AB∥CD,∠BCD=∠B=90°,
∴四边形ABCM是矩形,
∴AM=BC=8,CM=AB=10,
∵AD=10,
∴DM=,
∴CD=CM+DM=10+6=16;
(2)解:当四边形 PBQD 为平行四边形时,点P在AB上,点Q在DC上,如图:
由题意得:BP=10-3t,QD=2t,
∴10-3t=2t,解得:t=2;
此时BP=QD=4,CQ=12,
∴BQ=,
∴ 四边形PBQD 的周长=2(BP+BQ)=2(4+4)=8+8(cm);
(3)解:①当点P在线段AB上时,即0≤t≤时,如图:
S△BPQ=BP·BC=(10-3t)×8=20,解得:t=(秒);
②当点P在线段BC上时,即<t≤6时,如图:
BP=3t-10,CQ =16-2t,
S△BPQ=BP·CQ=(3t-10)×(16-2t)=20,
化简得:3t2-34t+100=0,
∵b2-4ac=-44<0,
∴方程没有实数根;
③当点P在线段CD上时,如图:
若点P在Q的右侧,即6≤t≤时,
PQ=34-5t,
S△BPQ=(34-5t)×8=20,解得:t=<6,(不符合题意,舍去);
若点P在Q的左侧,即<t≤8时,
PQ=5t-34,
S△BPQ=(5t-34)×8=20,解得:t=(秒).
综上可得: 所有满足条件的 t的值为:秒或秒.
【知识点】平行四边形的判定与性质;矩形的判定与性质;四边形-动点问题
21世纪教育网(www.21cnjy.com)
1 / 14
第18章平行四边形
一、单选题
1.如图,在平行四边形ABCD中,∠A:∠B=7:2,则∠A的度数是( )
A.110° B.140° C.120° D.160°
2.如图,E,F,G,H分别为四边形边的中点,要使四边形为矩形,应添加的条件是( )
A. B. C. D.
3.我们已经学过两种全等变换:平移和轴对称,通过变换可以把两条分散的线段拼接在一起.请借助变换解决下面问题:如图,四边形中,,,,则的最小值为( )
A.4 B.6 C. D.
4.如图,在平面直角坐标系中的位置如所示,顶点,,点B在x轴正半轴上,以点O为圆心,以小于长为半径作弧,分别交边,于点D,E,分别以点D,E为圆心,以大于长为半径作弧,两弧在内交于点F,作射线,交边于点G,则点G的坐标为( )
A. B. C. D.
5.在平行四边形中,,则的度数为( )
A. B. C. D.
6.如图,平行四边形的对角线AC,BD交于点O,已知BC=6,BD=12,AC=8,则△OAD的周长为( )
A.13 B.14 C.16 D.18
7.如图,平行四边形ABCD的对角线相交于点O,AO=4,OD=7,△DBC的周长比△ABC的周长( )
A.长6 B.短6 C.短3 D.长3
8.在中,对角线与交于点,在延长线上取一点,连接交于.已知,,,则的长等于( )
A. B. C. D.
9.如图,在 ABCD中,∠B是锐角,点F是AB边的中点,AE⊥BC于点E,连接DF,EF.若∠EFD=90°,AD=2,AB=,则AE长为( )
A.2 B. C. D.
10.如图,平行四边形 中, 、 相交于点 ,点 是 的中点,连接 并延长交 于点 , ,则下列 结论:① ;② ;⑧ ;④ ;其中一定正确的是( )
A.①②③④ B.①② C.②③④ D.①②③
二、填空题
11.如图,在中,点在上且,与交于点.若,则的长为 .
12.如图,在平面直角坐标系中,点,,将平行四边形OABC绕点O旋转90°后,点B的对应点坐标是 .
13.如图,矩形的面积为,对角线交于点O,以、为邻边作平行四边形,对角线交于点,以,为邻边作平行四边形……依此类推,则平行四边形的面积为 .
14.在平行四边形ABCD中,已知对角线AC和BD相交于点O,△ABO的周长为17,AB=6,那么对角线AC+BD= .
15.如图,在中,对角线,交于点,为中点,连接交于点,若的面积为1,则的面积为 .
16.如图,等边中,,为中点,,为边上的动点,且,则的最小值是 .
三、计算题
17.如图,一次函数与反比例函数的图象在第一象限的交点横坐标为1,直线轴于点,且与一次函数和反比例函数的图象分别交于点和点,且点在点上方.
(1)求反比例函数的表达式;
(2)若四边形是平行四边形,求的值.
18.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
19.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,满足,直线经过轴负半轴上的点,且.
(1)求直线的函数表达式;
(2)平移直线,平移后的直线与直线交于点,与轴交于点.
①已知平面内有一点,连接,当的值最小时,求的值;
②若平移后的直线与轴交于点,是否存在点,使以点为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
四、解答题
20.如图,在四边形中,,,,,点P从点D出发,以每秒1个单位长度的速度向点A运动,点Q从点B同时出发,以每秒2个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P运动时间为t秒.
(1)当点P运动停止时,______,线段的长为______;
(2)①用含t的式子填空:______,______,______;
② t为何值时,四边形为矩形,求出t的值;
(3)在运动的过程中,是否存在某一时刻t,使以P,D,C,Q为顶点的四边形为平行四边形?若存在,请求出t的值,若不存在,请说明理由.
21.如图,在 ABCD中,E、F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形,并证明.
22.如图,AM是的中线,是线段AM上一点(不与点A重合),DE//AB,交AC于点,交DF于点,连结AE.
(1)如图①,当点D与点M重合时,求证:四边形ABDE是平行四边形.
(2)如图②,当点D不与点M重合时,(1)中的结论还成立吗?请说明理由.
23.如图,在直角梯形 ABCD中,AB∥CD,∠BCD =90°,AB=AD=10cm,BC=8cm.点 P从点A 出发,以每秒 3c m的速度沿折线 ABCD 向点 D 运动,点 Q 从点 D 出发,以每秒 2cm 的速度沿线段 DC 向点 C 运动.已知动点 P,Q 同时出发,当点 Q运动到点C 时,P,Q两点同时停止运动,设运动时间为 t(s).
(1)求 CD的长.
(2)当四边形 PBQD 为平行四边形时,求四边形PBQD 的周长.
(3)在运动过程中,是否存在某一时刻,使得△BPQ的面积为 20 cm 若存在,请求出所有满足条件的 t的值;若不存在,请说明理由.
答案解析部分
1.【答案】C
【知识点】平行四边形的性质
2.【答案】D
【知识点】平行四边形的判定与性质;矩形的判定;三角形的中位线定理
3.【答案】D
【知识点】勾股定理;平行四边形的判定与性质
4.【答案】A
【知识点】坐标与图形性质;平行四边形的性质;尺规作图-作角的平分线;坐标系中的两点距离公式
5.【答案】B
【知识点】平行四边形的性质
6.【答案】C
【知识点】平行四边形的性质
7.【答案】A
【知识点】平行四边形的性质
8.【答案】B
【知识点】平行四边形的性质;相似三角形的判定与性质;三角形的中位线定理
9.【答案】B
【知识点】线段垂直平分线的性质;勾股定理;平行四边形的性质;三角形全等的判定-AAS
10.【答案】B
【知识点】平行四边形的性质;相似三角形的判定与性质;四边形的综合
11.【答案】
【知识点】平行四边形的性质;相似三角形的判定与性质
12.【答案】或
【知识点】平行四边形的性质;旋转的性质;坐标与图形变化﹣旋转
13.【答案】
【知识点】平行四边形的性质;矩形的性质;中心对称及中心对称图形
14.【答案】22
【知识点】平行四边形的性质
15.【答案】12
【知识点】平行四边形的性质;相似三角形的判定与性质
16.【答案】
【知识点】平行四边形的判定与性质;三角形的中位线定理
17.【答案】(1)
(2)
【知识点】反比例函数与一次函数的交点问题;平行四边形的性质
18.【答案】解:∵BC∥AD,CD∥AB,
∴四边形ABCD是平行四边形,
∴CD=AB=2,
∴S梯形OBCD==;
∴图中阴影部分的面积=S梯形OBCD-S扇形OBD=-×π×12=-。
【知识点】平行四边形的性质;平行四边形的判定;扇形面积的计算
19.【答案】(1)解:∵,
而,,
∴,,
解得:,,
∴,,
∴,
∵,,
∴,
∴,
∴,
设直线的函数表达式为,
将点,代入表达式可得:
可得,
解得:,
∴直线的函数表达式为.
(2)解:①根据题意,平移直线,平移后的直线与直线交于点,与轴交于点,∴可设直线的函数表达式为;
设直线的函数表达式为,
将点,代入,
可得,
解得:,
∴直线的函数表达式为:;
如下图,连接,
∵,
∴当点在同一直线上时,取最小值,
此时,设直线的解析式为,
将点,代入MC的解析式得:
可得,
解得:,
∴直线的解析式为,
联立解方程组,
得:,
∴,
∴将点代入直线表达式,
可得,
解得:;
②(Ⅰ)当点在点右侧时,如下图,过点作轴于点,
∵四边形为平行四边形,
∴,,
∴,
在△AOC和△EMD中,
∴,
∴,即,
将代入直线的表达式,
可得,解得,
∴,
∴将点代入直线表达式,
可得,解得,即;
(Ⅱ)当点在点左侧时,如下图,过点作轴于点,
∵四边形为平行四边形,
∴,,
∴,
在△AOC和△E ND 中,
∴,
∴,即,
将代入直线的表达式,
可得,解得,
∴,
∴将点代入直线表达式,
可得,解得,即.
综上可得,点的坐标为或.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题;平行四边形的性质;一次函数中的动态几何问题;一次函数图象的平移变换
20.【答案】(1);
(2)①;;;②
(3)
【知识点】平行四边形的性质;矩形的判定;一元一次方程的实际应用-几何问题
21.【答案】解:△ADF≌△CBE,
理由:∵四边形ABCD是平行四边形,
∴AD=BC,∠DAC=∠BCA,
∵BE∥DF,
∴∠DFC=∠BEA,
∴∠AFD=∠BEC,
在△ADF与CBE中,
,
∴△ADF≌△CBE(AAS).
【知识点】平行线的性质;平行四边形的性质;三角形全等的判定-AAS
22.【答案】(1)证明:如图1,∵AM是△ABC的中线,D与M重合,
∴DC=BD,
∵DE∥AB,
∴∠EDC=∠B,
∵CE∥AM,即CE∥AD,
∴∠ECD=∠ADB,
在△ECD和△ADB中,,
∴△ECD≌△ADB(ASA),
∴DE=AB,
∴四边形ABDE是平行四边形;
(2)解:(1)中的结论成立,
理由:如图2,过点M作MG∥AB交CE于点G,
∵DE∥AB,
∴MG∥DE,
∵CE∥AM,
∴四边形DEGM是平行四边形,
∴MG=DE,
同(1)得MG=AB,
∴DE=AB,
∴四边形ABDE是平行四边形.
【知识点】平行四边形的判定与性质;三角形全等的判定-ASA
23.【答案】(1)解:过点A作AM⊥CD于M,
∵AB∥CD,∠BCD=∠B=90°,
∴四边形ABCM是矩形,
∴AM=BC=8,CM=AB=10,
∵AD=10,
∴DM=,
∴CD=CM+DM=10+6=16;
(2)解:当四边形 PBQD 为平行四边形时,点P在AB上,点Q在DC上,如图:
由题意得:BP=10-3t,QD=2t,
∴10-3t=2t,解得:t=2;
此时BP=QD=4,CQ=12,
∴BQ=,
∴ 四边形PBQD 的周长=2(BP+BQ)=2(4+4)=8+8(cm);
(3)解:①当点P在线段AB上时,即0≤t≤时,如图:
S△BPQ=BP·BC=(10-3t)×8=20,解得:t=(秒);
②当点P在线段BC上时,即<t≤6时,如图:
BP=3t-10,CQ =16-2t,
S△BPQ=BP·CQ=(3t-10)×(16-2t)=20,
化简得:3t2-34t+100=0,
∵b2-4ac=-44<0,
∴方程没有实数根;
③当点P在线段CD上时,如图:
若点P在Q的右侧,即6≤t≤时,
PQ=34-5t,
S△BPQ=(34-5t)×8=20,解得:t=<6,(不符合题意,舍去);
若点P在Q的左侧,即<t≤8时,
PQ=5t-34,
S△BPQ=(5t-34)×8=20,解得:t=(秒).
综上可得: 所有满足条件的 t的值为:秒或秒.
【知识点】平行四边形的判定与性质;矩形的判定与性质;四边形-动点问题
21世纪教育网(www.21cnjy.com)
1 / 14
