19.1.1矩形的性质(含答案)
文档属性
| 名称 | 19.1.1矩形的性质(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 413.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-28 17:56:59 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
19.1.1矩形的性质
一、单选题
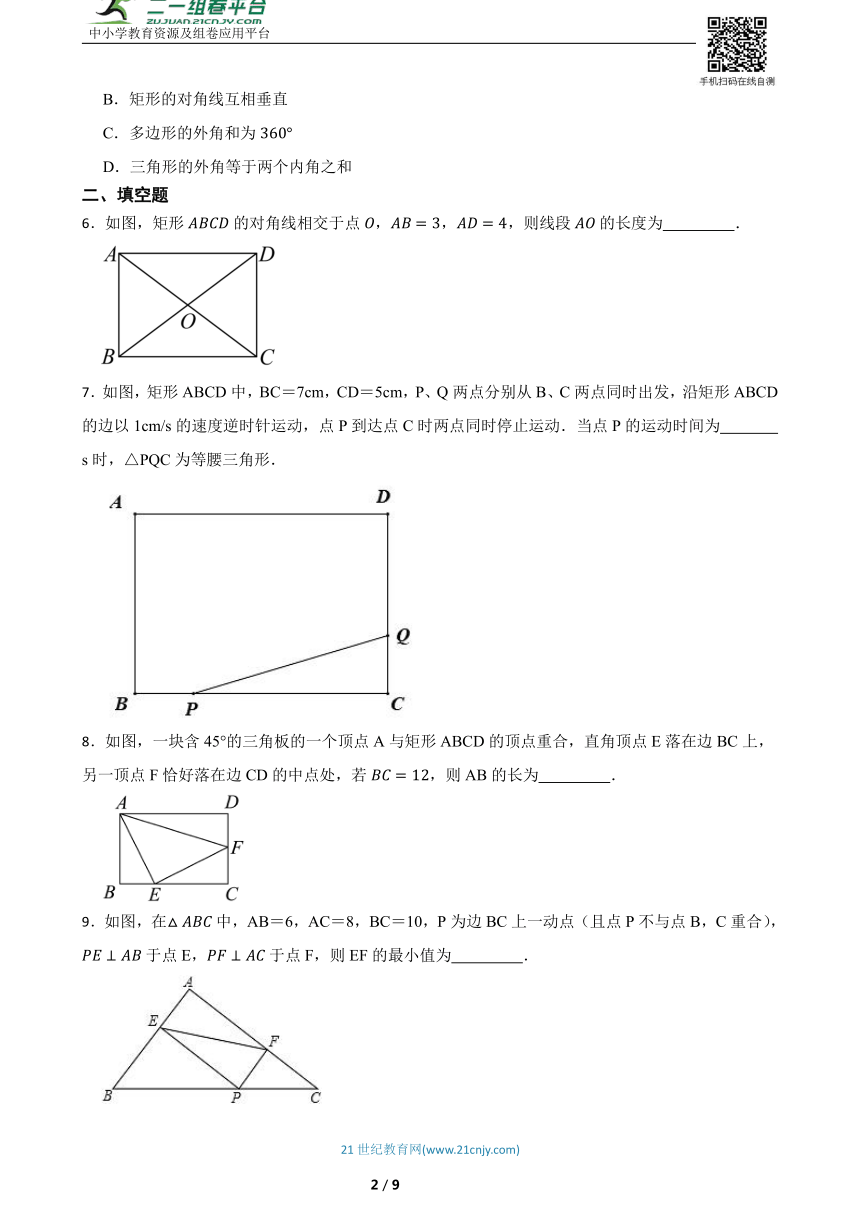
1.如图,四边形为矩形,对角线与交于点O,以下说法不一定正确的是( )
A. B. C. D.
2.如图,将矩形ABCD沿AC折叠,使点B落在点B'处,B'C交AD于点E,若∠1=25°,则∠2等于( )
A.25° B.30° C.50° D.60°
3.在矩形中,对角线相交于点O,的角平分线交于点E,若,则用表示为( )
A. B. C. D.
4.如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于( )
A. B. C. D.8
5.下列命题中,真命题是( )
A.平行四边形的对角线相等
B.矩形的对角线互相垂直
C.多边形的外角和为
D.三角形的外角等于两个内角之和
二、填空题
6.如图,矩形的对角线相交于点,,,则线段的长度为 .
7.如图,矩形ABCD中,BC=7cm,CD=5cm,P、Q两点分别从B、C两点同时出发,沿矩形ABCD的边以1cm/s的速度逆时针运动,点P到达点C时两点同时停止运动.当点P的运动时间为 s时,△PQC为等腰三角形.
8.如图,一块含45°的三角板的一个顶点A与矩形ABCD的顶点重合,直角顶点E落在边BC上,另一顶点F恰好落在边CD的中点处,若,则AB的长为 .
9.如图,在中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B,C重合),于点E,于点F,则EF的最小值为 .
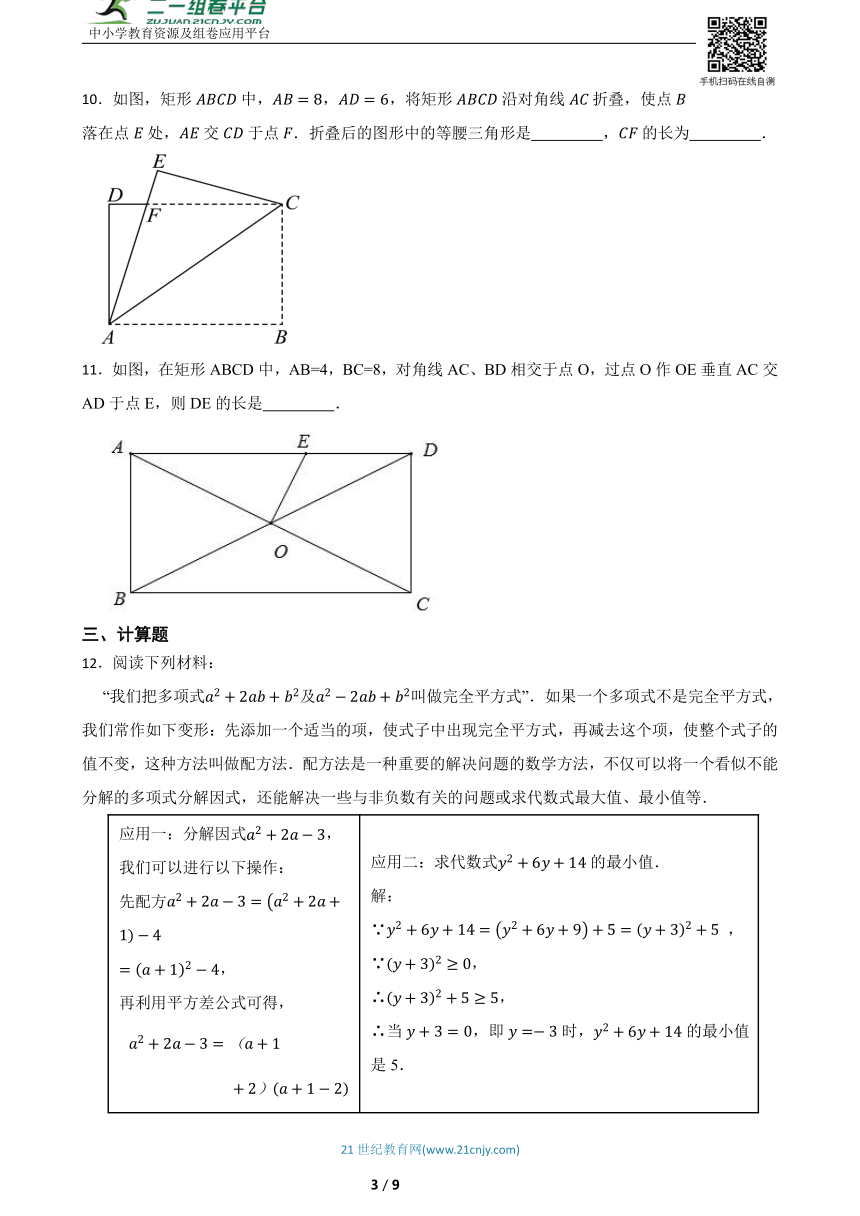
10.如图,矩形中,,,将矩形沿对角线折叠,使点落在点处,交于点.折叠后的图形中的等腰三角形是 ,的长为 .
11.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是 .
三、计算题
12.阅读下列材料:
“我们把多项式及叫做完全平方式”.如果一个多项式不是完全平方式,我们常作如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等.
应用一:分解因式, 我们可以进行以下操作: 先配方 , 再利用平方差公式可得, . 应用二:求代数式的最小值. 解:∵ , ∵, ∴, ∴当,即时,的最小值是5.
【问题解决】
(1)分解因式: ;
(2)代数式的最小值 ;
(3)某养殖场要将一块长为8米,宽为4米的矩形养殖区域进行改造,使得长减少x米,宽增加x米,请问:当x取何值时,矩形区域的面积S最大?最大值是多少?
13.课本再现:
(1)如图,在矩形中,,,是上不与和重合的一个动点,过点分别作和的垂线,垂足分别为,.求的值.
如图1,连接,利用与的面积之和是矩形面积的,可求出的值,请你写出求解过程;
知识应用:
(2)如图2,在矩形中,点,分别在边,上,将矩形沿直线折叠,使点恰好与点重合,点落在点处.点为线段上一动点(不与点,重合),过点分别作直线,的垂线,垂足分别为和,以,为邻边作平行四边形,若,,求平行四边形的周长;
(3)如图3,当点是等边外一点时,过点分别作直线、、的垂线、垂足分别为点、、.若,请直接写出的面积.
四、解答题
14.如图,在矩形中,.动点P、Q分别从点A、C以的速度同时出发.动点P沿向终点B运动,动点Q沿向终点D运动,交对角线于点O.设点P的运动时间为t(秒).
(1)用含t的式子表示:______,______;
(2)运动过程中,无论t为何值,四边形的面积______;
(3)当四边形是矩形时,求出t的值.
五、作图题
15.已知四边形为矩形,点是边的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
(1)在图1中作出矩形的对称轴,使;
(2)在图2中作出矩形的对称轴,使.
六、综合题
16.如图,在矩形中,,点P从点A出发沿以的速度向点B运动;同时,点Q从点B出发沿以的速度向点C运动,点P运动到点B时,点Q也停止运动;当的面积等于时,求运动时间.
17.如图,八里庄孙大伯要修一个育苗棚,棚的横截面是直角三角形,棚宽,高 ,长,求覆盖在顶上的长方形塑料薄膜需多少平方米(结果保留小数点后一位).参考数据:.
18.如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:△DEF是等腰三角形.
答案解析部分
1.【答案】C
【知识点】矩形的性质
2.【答案】C
【知识点】矩形的性质
3.【答案】B
【知识点】三角形的外角性质;等腰三角形的性质;矩形的性质
4.【答案】A
【知识点】矩形的性质
5.【答案】C
【知识点】多边形内角与外角;平行四边形的性质;矩形的性质;真命题与假命题
6.【答案】
【知识点】勾股定理;矩形的性质
7.【答案】或
【知识点】矩形的性质;一元一次方程的实际应用-几何问题
8.【答案】8
【知识点】勾股定理;矩形的性质
9.【答案】4.8
【知识点】勾股定理的逆定理;矩形的性质
10.【答案】;
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质
11.【答案】3
【知识点】线段垂直平分线的性质;勾股定理;矩形的性质
12.【答案】(1);
(2)2;
(3)当x取2时,矩形区域的面积S最大,最大值是36.
【知识点】完全平方公式及运用;因式分解的应用;矩形的性质
13.【答案】(1);(2)24;(3)
【知识点】勾股定理;矩形的性质
14.【答案】(1)cm,cm
(2)24
(3)2
【知识点】勾股定理;矩形的性质
15.【答案】(1)解:如图1中,直线即为所求;
(2)解:如图2中,直线即为所求;
【知识点】矩形的性质;作图-平行线
16.【答案】
【知识点】矩形的性质
17.【答案】
【知识点】勾股定理;矩形的性质
18.【答案】(1)解:∵四边形ABCD是矩形,∴AD=BC,AB=CD.
由折叠的性质可得:BC=CE,AB=AE,
∴AD=CE,AE=CD.
在△ADE和△CED中, ,
∴△ADE≌△CED(SSS)
(2)解:由(1)得△ADE≌△CED,
∴∠DEA=∠EDC,即∠DEF=∠EDF,
∴EF=DF,
∴△DEF是等腰三角形
【知识点】全等三角形的判定与性质;矩形的性质;翻折变换(折叠问题)
21世纪教育网(www.21cnjy.com)
1 / 9
19.1.1矩形的性质
一、单选题
1.如图,四边形为矩形,对角线与交于点O,以下说法不一定正确的是( )
A. B. C. D.
2.如图,将矩形ABCD沿AC折叠,使点B落在点B'处,B'C交AD于点E,若∠1=25°,则∠2等于( )
A.25° B.30° C.50° D.60°
3.在矩形中,对角线相交于点O,的角平分线交于点E,若,则用表示为( )
A. B. C. D.
4.如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于( )
A. B. C. D.8
5.下列命题中,真命题是( )
A.平行四边形的对角线相等
B.矩形的对角线互相垂直
C.多边形的外角和为
D.三角形的外角等于两个内角之和
二、填空题
6.如图,矩形的对角线相交于点,,,则线段的长度为 .
7.如图,矩形ABCD中,BC=7cm,CD=5cm,P、Q两点分别从B、C两点同时出发,沿矩形ABCD的边以1cm/s的速度逆时针运动,点P到达点C时两点同时停止运动.当点P的运动时间为 s时,△PQC为等腰三角形.
8.如图,一块含45°的三角板的一个顶点A与矩形ABCD的顶点重合,直角顶点E落在边BC上,另一顶点F恰好落在边CD的中点处,若,则AB的长为 .
9.如图,在中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B,C重合),于点E,于点F,则EF的最小值为 .
10.如图,矩形中,,,将矩形沿对角线折叠,使点落在点处,交于点.折叠后的图形中的等腰三角形是 ,的长为 .
11.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是 .
三、计算题
12.阅读下列材料:
“我们把多项式及叫做完全平方式”.如果一个多项式不是完全平方式,我们常作如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等.
应用一:分解因式, 我们可以进行以下操作: 先配方 , 再利用平方差公式可得, . 应用二:求代数式的最小值. 解:∵ , ∵, ∴, ∴当,即时,的最小值是5.
【问题解决】
(1)分解因式: ;
(2)代数式的最小值 ;
(3)某养殖场要将一块长为8米,宽为4米的矩形养殖区域进行改造,使得长减少x米,宽增加x米,请问:当x取何值时,矩形区域的面积S最大?最大值是多少?
13.课本再现:
(1)如图,在矩形中,,,是上不与和重合的一个动点,过点分别作和的垂线,垂足分别为,.求的值.
如图1,连接,利用与的面积之和是矩形面积的,可求出的值,请你写出求解过程;
知识应用:
(2)如图2,在矩形中,点,分别在边,上,将矩形沿直线折叠,使点恰好与点重合,点落在点处.点为线段上一动点(不与点,重合),过点分别作直线,的垂线,垂足分别为和,以,为邻边作平行四边形,若,,求平行四边形的周长;
(3)如图3,当点是等边外一点时,过点分别作直线、、的垂线、垂足分别为点、、.若,请直接写出的面积.
四、解答题
14.如图,在矩形中,.动点P、Q分别从点A、C以的速度同时出发.动点P沿向终点B运动,动点Q沿向终点D运动,交对角线于点O.设点P的运动时间为t(秒).
(1)用含t的式子表示:______,______;
(2)运动过程中,无论t为何值,四边形的面积______;
(3)当四边形是矩形时,求出t的值.
五、作图题
15.已知四边形为矩形,点是边的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.
(1)在图1中作出矩形的对称轴,使;
(2)在图2中作出矩形的对称轴,使.
六、综合题
16.如图,在矩形中,,点P从点A出发沿以的速度向点B运动;同时,点Q从点B出发沿以的速度向点C运动,点P运动到点B时,点Q也停止运动;当的面积等于时,求运动时间.
17.如图,八里庄孙大伯要修一个育苗棚,棚的横截面是直角三角形,棚宽,高 ,长,求覆盖在顶上的长方形塑料薄膜需多少平方米(结果保留小数点后一位).参考数据:.
18.如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:△DEF是等腰三角形.
答案解析部分
1.【答案】C
【知识点】矩形的性质
2.【答案】C
【知识点】矩形的性质
3.【答案】B
【知识点】三角形的外角性质;等腰三角形的性质;矩形的性质
4.【答案】A
【知识点】矩形的性质
5.【答案】C
【知识点】多边形内角与外角;平行四边形的性质;矩形的性质;真命题与假命题
6.【答案】
【知识点】勾股定理;矩形的性质
7.【答案】或
【知识点】矩形的性质;一元一次方程的实际应用-几何问题
8.【答案】8
【知识点】勾股定理;矩形的性质
9.【答案】4.8
【知识点】勾股定理的逆定理;矩形的性质
10.【答案】;
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质
11.【答案】3
【知识点】线段垂直平分线的性质;勾股定理;矩形的性质
12.【答案】(1);
(2)2;
(3)当x取2时,矩形区域的面积S最大,最大值是36.
【知识点】完全平方公式及运用;因式分解的应用;矩形的性质
13.【答案】(1);(2)24;(3)
【知识点】勾股定理;矩形的性质
14.【答案】(1)cm,cm
(2)24
(3)2
【知识点】勾股定理;矩形的性质
15.【答案】(1)解:如图1中,直线即为所求;
(2)解:如图2中,直线即为所求;
【知识点】矩形的性质;作图-平行线
16.【答案】
【知识点】矩形的性质
17.【答案】
【知识点】勾股定理;矩形的性质
18.【答案】(1)解:∵四边形ABCD是矩形,∴AD=BC,AB=CD.
由折叠的性质可得:BC=CE,AB=AE,
∴AD=CE,AE=CD.
在△ADE和△CED中, ,
∴△ADE≌△CED(SSS)
(2)解:由(1)得△ADE≌△CED,
∴∠DEA=∠EDC,即∠DEF=∠EDF,
∴EF=DF,
∴△DEF是等腰三角形
【知识点】全等三角形的判定与性质;矩形的性质;翻折变换(折叠问题)
21世纪教育网(www.21cnjy.com)
1 / 9
