19.1矩形(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
19.1矩形
一、单选题
1.如图,把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,若,则截面的半径等于( )
A. B. C. D.
2.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4,则BC的长是( )
A.2 B.3 C.2 D.3
3.如图,矩形中,,E是的中点,,则长为( )
A. B.2 C. D.3
4.矩形具有而一般平行四边形不具有的性质是( )。
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
5.如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合折痕为EF,则△ABE的面积为( )
A.3cm B.4cm C.6cm D.12cm
二、填空题
6.如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则= .
7.如图,将矩形沿对角线折叠,点B落在点E处,若平分,则的长为 .
8.如图,在中,为斜边上一动点,,,若,,则线段的最小值为 .
9.如图,在中,,是的重心,若,则 .
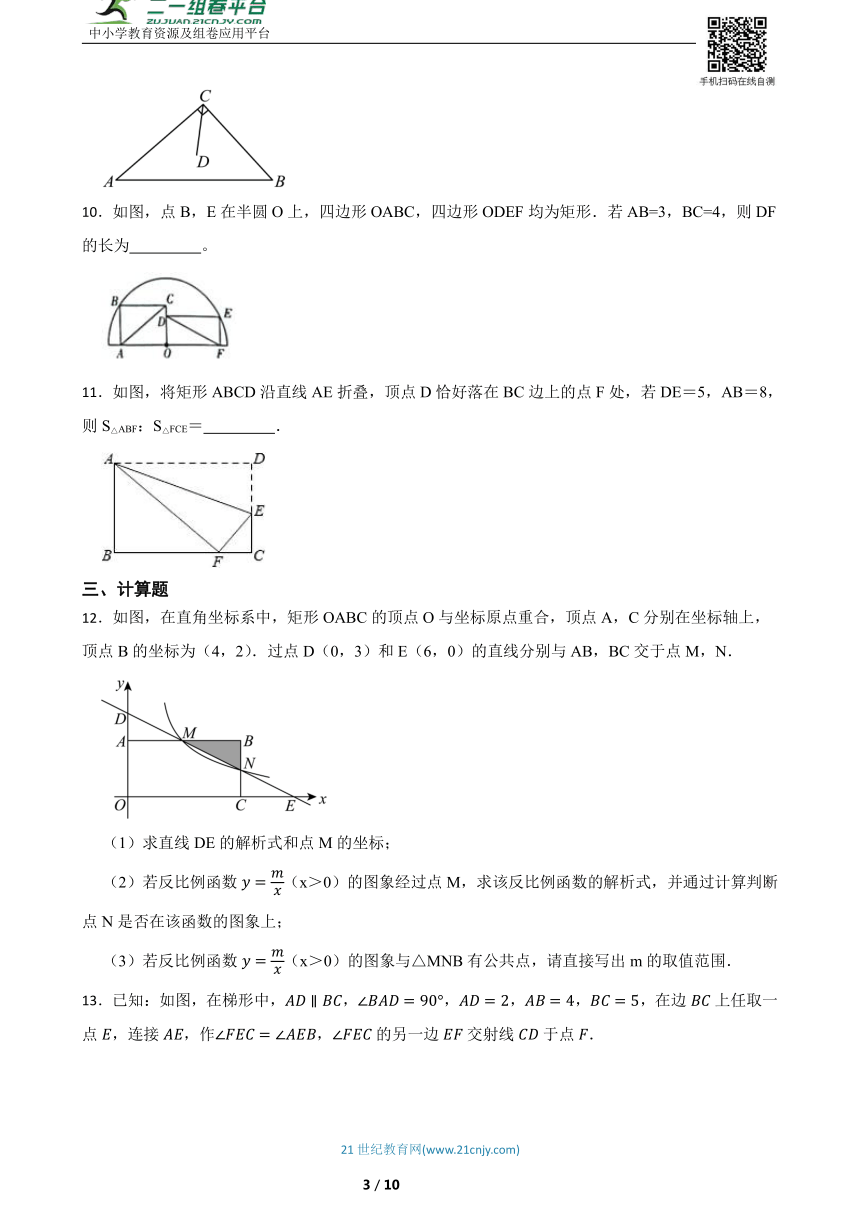
10.如图,点B,E在半圆O上,四边形OABC,四边形ODEF均为矩形.若AB=3,BC=4,则DF的长为 。
11.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,若DE=5,AB=8,则S△ABF:S△FCE= .
三、计算题
12.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
13.已知:如图,在梯形中,,,,,,在边上任取一点,连接,作,的另一边交射线于点.
(1)求的值;
(2)如图,当点在线段上时,若,求的长;
(3)连接,当是直角三角形时,直接写出BE的长.
14.【问题提出】
(1)如图①,为半圆的直径,O为圆心,C,D为半圆上的两点,若,,则___.
【问题探究】
(2)如图②,在矩形中,,,点P在直线的右侧,且满足,求点P到的最短距离.
【问题解决】
(3)如图③,有一块矩形型板材,米,米,由于工作需要,工人王师傅想在这块板材上找一点P,裁出与,并满足,.请问王师傅的设想可以实现吗?如果可以,请帮他计算所裁得的的面积;如果不能,请说明你的理由.
四、解答题
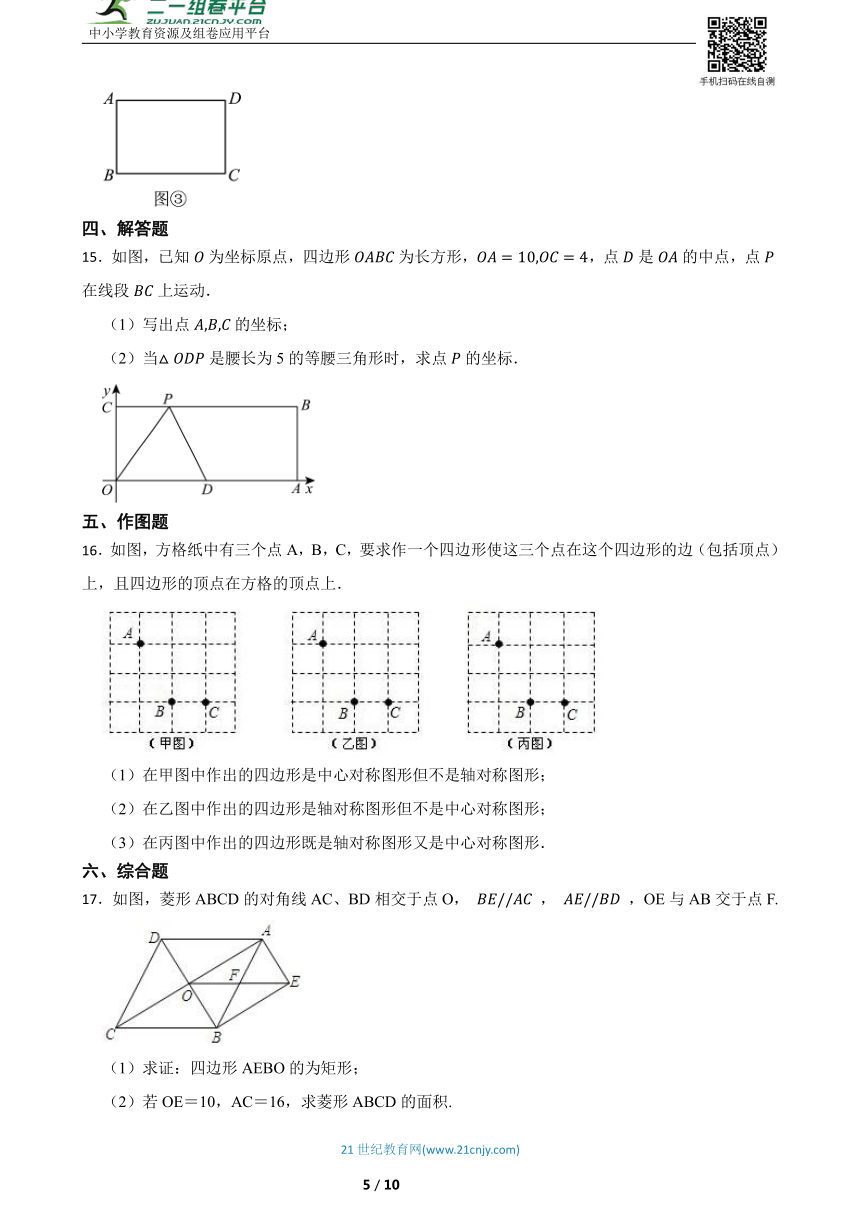
15.如图,已知为坐标原点,四边形为长方形,,点是的中点,点在线段上运动.
(1)写出点的坐标;
(2)当是腰长为5的等腰三角形时,求点的坐标.
五、作图题
16.如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
六、综合题
17.如图,菱形ABCD的对角线AC、BD相交于点O, , ,OE与AB交于点F.
(1)求证:四边形AEBO的为矩形;
(2)若OE=10,AC=16,求菱形ABCD的面积.
18.某校数学活动小组的同学要借助无人机测量某山坡上信号塔顶端到地面的距离.
活动内容 测量信号塔顶端到地面的距离
活动目的 运用锐角三角函数知识解决实际问题
测量工具 无人机、测量角度的仪器、皮尺等
测量示意图 说明:如图为信号塔和建筑物的侧面示意图,点在同一平面内,点在同一水平线上,建筑物为矩形.
测量数据 ①从点处观测点的俯角
②从点处观测点的俯角
③从点处观测点的俯角
④建筑物的宽度
⑤建筑物的高度
参考数据 ,, ,
计算信号塔顶端到地面的距离 要求:①结果保留到; ②先选择合适的测量数据,再进行计算.
19.如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
(1)如果∠BAC=90°,那么四边形AEDF是 形;
(2)如果AD是△ABC的角平分线,那么四边形AEDF是 形.
七、实践探究题
20.某“综合与实践”小组开展测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量,测量报告如下.
课题 测量旗杆的高度
成员 组长:××× 组员:×××,×××,×××
测量工具 皮尺,标杆
测量示意图 说明:在水平地面上直立一根标杆,观测者沿着直线后退到点,使眼睛、标杆的顶端、旗杆的顶端在同一直线上.
测量数据 观测者与标杆的距离 观测者与旗杆的距离 标杆的长 观测者的眼睛离地面的距离
问题解决 如图,过点作于点,交于点.
请根据以上测量结果及该小组的思路,求学校旗杆的高度.
答案解析部分
1.【答案】C
【知识点】勾股定理;矩形的判定与性质;垂径定理
2.【答案】C
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质
3.【答案】C
【知识点】含30°角的直角三角形;勾股定理;矩形的性质;直角三角形斜边上的中线
4.【答案】C
【知识点】矩形的性质
5.【答案】C
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
6.【答案】
【知识点】等边三角形的性质;矩形的性质
7.【答案】
【知识点】含30°角的直角三角形;勾股定理;矩形的性质
8.【答案】
【知识点】勾股定理;矩形的判定与性质
9.【答案】
【知识点】矩形的判定与性质;三角形的重心及应用;三角形的中位线定理
10.【答案】5
【知识点】勾股定理;矩形的性质
11.【答案】4
【知识点】矩形的性质;相似三角形的判定与性质
12.【答案】(1),M(2,2)
(2),在
(3)4≤ m ≤8
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;矩形的性质
13.【答案】(1)
(2)
(3)或或
【知识点】矩形的判定与性质;相似三角形的判定与性质;解直角三角形
14.【答案】(1);(2);(3)师傅的设想可以实现,平方米
【知识点】矩形的性质;圆周角定理;相似三角形的判定与性质;解直角三角形
15.【答案】(1)A(10,0),B(10,4),C(0,4);(2)(3,4)或(2,4)或(8,4).
【知识点】等腰三角形的性质;勾股定理;矩形的性质
16.【答案】(1)解:甲图:平行四边形
(2)解:乙图:等腰梯形
(3)解:丙图:正方形
【知识点】平行四边形的性质;矩形的性质;正方形的性质;等腰梯形的性质
17.【答案】(1)证明:∵ , ,
∴四边形AEBO为平行四边形,
又∵四边形ABCD为菱形,
∴ ,
∴ ,
∴平行四边形AEBO为矩形
(2)解:∵四边形AEBO为矩形,
∴AB=OE=10,
又∵四边形ABCD为菱形,
∴AO= AC=8,
∴ ,
∴ ,
∴BD=2BO=12,
∴菱形ABCD的面积= .
【知识点】勾股定理;平行四边形的判定;菱形的性质;矩形的判定
18.【答案】选择数据①③⑤,信号塔顶端到地面的距离约为
【知识点】矩形的判定与性质;解直角三角形的实际应用﹣仰角俯角问题
19.【答案】(1)矩
(2)菱
【知识点】菱形的判定;矩形的判定
20.【答案】
【知识点】矩形的性质;相似三角形的应用
21世纪教育网(www.21cnjy.com)
1 / 10
19.1矩形
一、单选题
1.如图,把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,若,则截面的半径等于( )
A. B. C. D.
2.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AC=4,则BC的长是( )
A.2 B.3 C.2 D.3
3.如图,矩形中,,E是的中点,,则长为( )
A. B.2 C. D.3
4.矩形具有而一般平行四边形不具有的性质是( )。
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
5.如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合折痕为EF,则△ABE的面积为( )
A.3cm B.4cm C.6cm D.12cm
二、填空题
6.如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则= .
7.如图,将矩形沿对角线折叠,点B落在点E处,若平分,则的长为 .
8.如图,在中,为斜边上一动点,,,若,,则线段的最小值为 .
9.如图,在中,,是的重心,若,则 .
10.如图,点B,E在半圆O上,四边形OABC,四边形ODEF均为矩形.若AB=3,BC=4,则DF的长为 。
11.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,若DE=5,AB=8,则S△ABF:S△FCE= .
三、计算题
12.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
13.已知:如图,在梯形中,,,,,,在边上任取一点,连接,作,的另一边交射线于点.
(1)求的值;
(2)如图,当点在线段上时,若,求的长;
(3)连接,当是直角三角形时,直接写出BE的长.
14.【问题提出】
(1)如图①,为半圆的直径,O为圆心,C,D为半圆上的两点,若,,则___.
【问题探究】
(2)如图②,在矩形中,,,点P在直线的右侧,且满足,求点P到的最短距离.
【问题解决】
(3)如图③,有一块矩形型板材,米,米,由于工作需要,工人王师傅想在这块板材上找一点P,裁出与,并满足,.请问王师傅的设想可以实现吗?如果可以,请帮他计算所裁得的的面积;如果不能,请说明你的理由.
四、解答题
15.如图,已知为坐标原点,四边形为长方形,,点是的中点,点在线段上运动.
(1)写出点的坐标;
(2)当是腰长为5的等腰三角形时,求点的坐标.
五、作图题
16.如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
六、综合题
17.如图,菱形ABCD的对角线AC、BD相交于点O, , ,OE与AB交于点F.
(1)求证:四边形AEBO的为矩形;
(2)若OE=10,AC=16,求菱形ABCD的面积.
18.某校数学活动小组的同学要借助无人机测量某山坡上信号塔顶端到地面的距离.
活动内容 测量信号塔顶端到地面的距离
活动目的 运用锐角三角函数知识解决实际问题
测量工具 无人机、测量角度的仪器、皮尺等
测量示意图 说明:如图为信号塔和建筑物的侧面示意图,点在同一平面内,点在同一水平线上,建筑物为矩形.
测量数据 ①从点处观测点的俯角
②从点处观测点的俯角
③从点处观测点的俯角
④建筑物的宽度
⑤建筑物的高度
参考数据 ,, ,
计算信号塔顶端到地面的距离 要求:①结果保留到; ②先选择合适的测量数据,再进行计算.
19.如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
(1)如果∠BAC=90°,那么四边形AEDF是 形;
(2)如果AD是△ABC的角平分线,那么四边形AEDF是 形.
七、实践探究题
20.某“综合与实践”小组开展测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量,测量报告如下.
课题 测量旗杆的高度
成员 组长:××× 组员:×××,×××,×××
测量工具 皮尺,标杆
测量示意图 说明:在水平地面上直立一根标杆,观测者沿着直线后退到点,使眼睛、标杆的顶端、旗杆的顶端在同一直线上.
测量数据 观测者与标杆的距离 观测者与旗杆的距离 标杆的长 观测者的眼睛离地面的距离
问题解决 如图,过点作于点,交于点.
请根据以上测量结果及该小组的思路,求学校旗杆的高度.
答案解析部分
1.【答案】C
【知识点】勾股定理;矩形的判定与性质;垂径定理
2.【答案】C
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质
3.【答案】C
【知识点】含30°角的直角三角形;勾股定理;矩形的性质;直角三角形斜边上的中线
4.【答案】C
【知识点】矩形的性质
5.【答案】C
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
6.【答案】
【知识点】等边三角形的性质;矩形的性质
7.【答案】
【知识点】含30°角的直角三角形;勾股定理;矩形的性质
8.【答案】
【知识点】勾股定理;矩形的判定与性质
9.【答案】
【知识点】矩形的判定与性质;三角形的重心及应用;三角形的中位线定理
10.【答案】5
【知识点】勾股定理;矩形的性质
11.【答案】4
【知识点】矩形的性质;相似三角形的判定与性质
12.【答案】(1),M(2,2)
(2),在
(3)4≤ m ≤8
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;矩形的性质
13.【答案】(1)
(2)
(3)或或
【知识点】矩形的判定与性质;相似三角形的判定与性质;解直角三角形
14.【答案】(1);(2);(3)师傅的设想可以实现,平方米
【知识点】矩形的性质;圆周角定理;相似三角形的判定与性质;解直角三角形
15.【答案】(1)A(10,0),B(10,4),C(0,4);(2)(3,4)或(2,4)或(8,4).
【知识点】等腰三角形的性质;勾股定理;矩形的性质
16.【答案】(1)解:甲图:平行四边形
(2)解:乙图:等腰梯形
(3)解:丙图:正方形
【知识点】平行四边形的性质;矩形的性质;正方形的性质;等腰梯形的性质
17.【答案】(1)证明:∵ , ,
∴四边形AEBO为平行四边形,
又∵四边形ABCD为菱形,
∴ ,
∴ ,
∴平行四边形AEBO为矩形
(2)解:∵四边形AEBO为矩形,
∴AB=OE=10,
又∵四边形ABCD为菱形,
∴AO= AC=8,
∴ ,
∴ ,
∴BD=2BO=12,
∴菱形ABCD的面积= .
【知识点】勾股定理;平行四边形的判定;菱形的性质;矩形的判定
18.【答案】选择数据①③⑤,信号塔顶端到地面的距离约为
【知识点】矩形的判定与性质;解直角三角形的实际应用﹣仰角俯角问题
19.【答案】(1)矩
(2)菱
【知识点】菱形的判定;矩形的判定
20.【答案】
【知识点】矩形的性质;相似三角形的应用
21世纪教育网(www.21cnjy.com)
1 / 10
