19.2.1菱形的性质(含答案)
文档属性
| 名称 | 19.2.1菱形的性质(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 325.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-28 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
19.2.1菱形的性质
一、单选题
1.下列结论中,矩形具有而菱形不一定具有的性质是( )
A.对边相等 B.对角线互相平分
C.对角线互相垂直 D.对角线相等
2.如图,在菱形中,,则的度数为( )
A. B. C. D.
3.如图,点是内的一点,过点作直线、分别平行于、,与的边分别交于、、、.则图中平行四边形的个数为( )
A.10个 B.9个 C.8个 D.7个
4.菱形不具有的性质是( )
A.四条边都相等 B.四个角都相等
C.对角线互相垂直 D.对角线互相平分
5.如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.2S1=S2
二、填空题
6.如图,在菱形ABCD中,对角线AC、BD交于点O,若BD=7,AC=4,则菱形ABCD的面积为 .
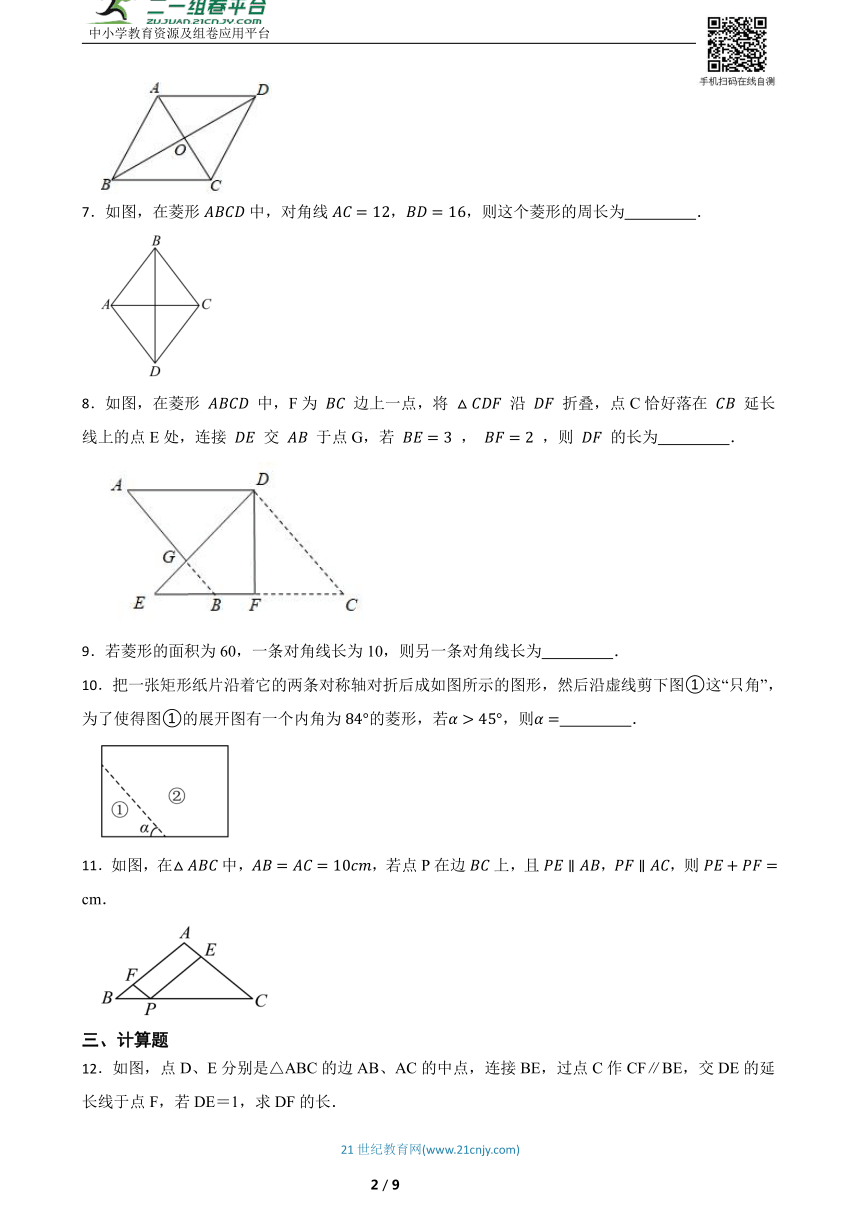
7.如图,在菱形中,对角线,,则这个菱形的周长为 .
8.如图,在菱形 中,F为 边上一点,将 沿 折叠,点C恰好落在 延长线上的点E处,连接 交 于点G,若 , ,则 的长为 .
9.若菱形的面积为60,一条对角线长为10,则另一条对角线长为 .
10.把一张矩形纸片沿着它的两条对称轴对折后成如图所示的图形,然后沿虚线剪下图①这“只角”,为了使得图①的展开图有一个内角为的菱形,若,则 .
11.如图,在中,,若点P在边上,且,,则 cm.
三、计算题
12.如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长.
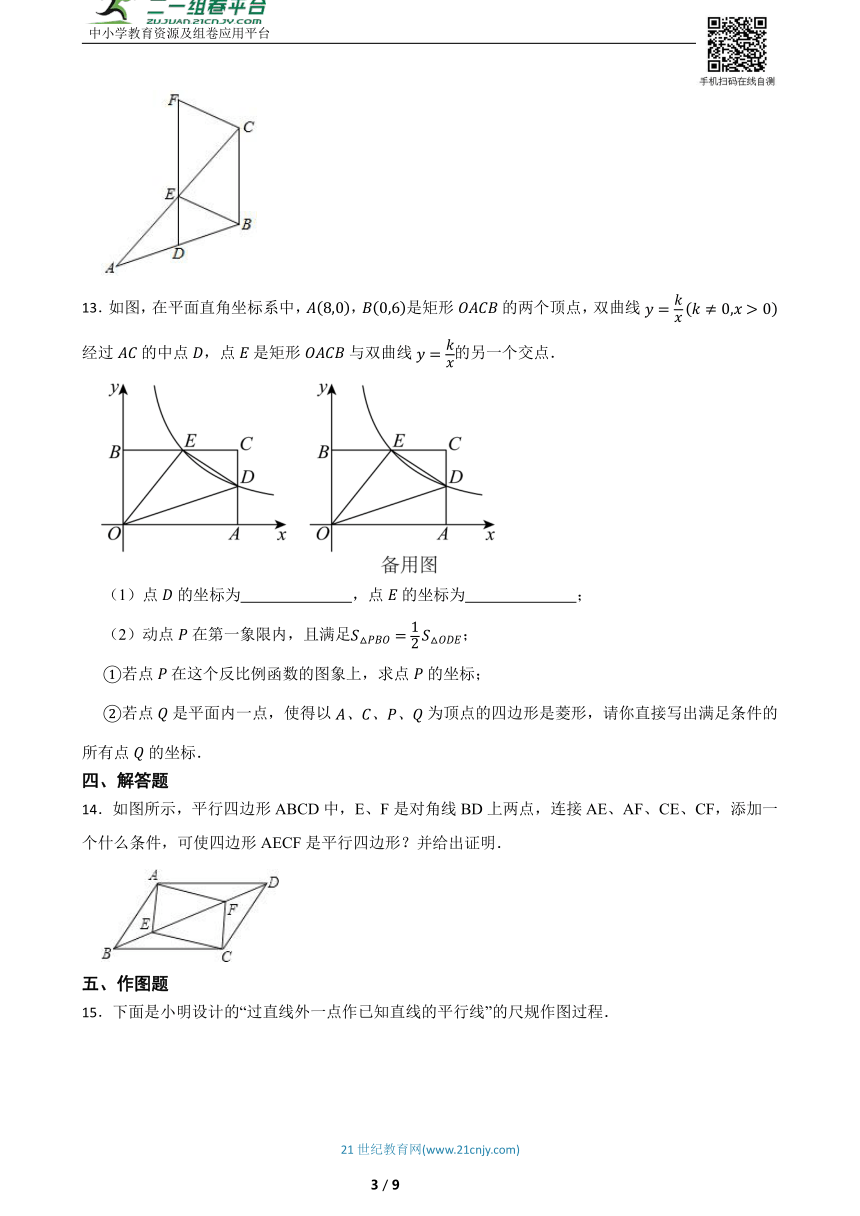
13.如图,在平面直角坐标系中,,是矩形的两个顶点,双曲线经过的中点,点是矩形与双曲线的另一个交点.
(1)点的坐标为 ,点的坐标为 ;
(2)动点在第一象限内,且满足;
若点在这个反比例函数的图象上,求点的坐标;
若点是平面内一点,使得以为顶点的四边形是菱形,请你直接写出满足条件的所有点的坐标.
四、解答题
14.如图所示,平行四边形ABCD中,E、F是对角线BD上两点,连接AE、AF、CE、CF,添加一个什么条件,可使四边形AECF是平行四边形?并给出证明.
五、作图题
15.下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:如图1,直线l 及直线l 外一点A.
求作:直线AD,使得AD// l.
作法:如图2,
①在直线l 上任取两点B,C,连接AB;
②分别以点A,C 为圆心,线段BC,AB 长为半径画弧,两弧在直线l 上方相交于点D;
③作直线AD.
直线AD 就是所求作的直线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接CD.
∵ AB =▲,BC =▲,
∴ 四边形ABCD 为平行四边形( )(填推理的依据).
∴ AD// l.
六、综合题
16.如图,在梯形ABCD中,AB∥CD.
(1)已知∠A=∠B,求证:AD=BC;
(2)已知AD=BC,求证:∠A=∠B.
17.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.
(1)求证:AE=BF;
(2)若点E恰好是AD的中点,AB=2,求BD的值.
18.如图,某型号千斤顶的工作原理是利用四边形的不稳定性,图中的菱形是该型号千斤顶的示意图,保持菱形边长不变,可通过改变的长来调节的长.已知,的初始长为,如果要使的长达到,那么的长需要缩短多少.
答案解析部分
1.【答案】D
【知识点】菱形的性质;矩形的性质
2.【答案】C
【知识点】平行线的性质;菱形的性质
3.【答案】B
【知识点】平行四边形的性质;平行四边形的判定与性质
4.【答案】B
【知识点】菱形的性质
5.【答案】B
【知识点】平行四边形的判定与性质
6.【答案】14
【知识点】菱形的性质
7.【答案】40
【知识点】勾股定理;菱形的性质
8.【答案】
【知识点】菱形的性质;翻折变换(折叠问题)
9.【答案】12
【知识点】菱形的性质
10.【答案】
【知识点】菱形的性质
11.【答案】10
【知识点】等腰三角形的判定;平行四边形的判定与性质
12.【答案】解:∵D、E分别是边、的中点
∴ ∥
∵
∴
∵∥
∴四边形为平行四边形
∴
∴.
【知识点】平行四边形的判定与性质
13.【答案】(1),;
(2);或或或.
【知识点】勾股定理;菱形的性质;矩形的性质
14.【答案】可添加BE=DF(或AE=CF等).
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵BE=DF,
∴△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴∠AEF=CFE,
∴AE∥CF,
∴四边形AECF是平行四边形 (其他证方法:连对角线等 )
【知识点】全等三角形的判定与性质;平行四边形的判定与性质
15.【答案】(1)解:如图所示,
(2)证明:连接CD.
∵ AB =CD,BC =AD,
∴ 四边形ABCD 为平行四边形(两组对边分别相等的四边形是平行四边形)(填推理的依据).
∴ AD// l.
故答案为:,,两组对边分别相等的四边形是平行四边形.
【知识点】平行四边形的判定与性质;作图-平行线
16.【答案】(1)解:如图,过点C作CE∥DA,交AB于点E
∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵CE∥DA
∴∠A=∠CEB
又∵∠A=∠B
∴∠CEB=∠B
∴EC=BC
∴AD=BC
(2)解:∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵AD=BC
∴EC=BC
∴∠CEB=∠B
又∵CE∥DA
∴∠CEB=∠A
∴∠B=∠A
【知识点】等式的基本性质;等腰三角形的性质;平行四边形的判定与性质
17.【答案】(1)证明:四边形ABCD是菱形
∴AB=BC,AD∥BC
∴∠A=∠CBF
∵BE⊥AD、CF⊥AB
∴∠AEB=∠BFC=90°
∴△AEB≌△BFC(AAS)
∴AE=BF
(2)解:∵E是AD中点,且BE⊥AD
∴直线BE为AD的垂直平分线
∴BD=AB=2
【知识点】线段垂直平分线的性质;菱形的性质
18.【答案】的长需要缩短
【知识点】勾股定理;菱形的性质
21世纪教育网(www.21cnjy.com)
1 / 9
19.2.1菱形的性质
一、单选题
1.下列结论中,矩形具有而菱形不一定具有的性质是( )
A.对边相等 B.对角线互相平分
C.对角线互相垂直 D.对角线相等
2.如图,在菱形中,,则的度数为( )
A. B. C. D.
3.如图,点是内的一点,过点作直线、分别平行于、,与的边分别交于、、、.则图中平行四边形的个数为( )
A.10个 B.9个 C.8个 D.7个
4.菱形不具有的性质是( )
A.四条边都相等 B.四个角都相等
C.对角线互相垂直 D.对角线互相平分
5.如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.2S1=S2
二、填空题
6.如图,在菱形ABCD中,对角线AC、BD交于点O,若BD=7,AC=4,则菱形ABCD的面积为 .
7.如图,在菱形中,对角线,,则这个菱形的周长为 .
8.如图,在菱形 中,F为 边上一点,将 沿 折叠,点C恰好落在 延长线上的点E处,连接 交 于点G,若 , ,则 的长为 .
9.若菱形的面积为60,一条对角线长为10,则另一条对角线长为 .
10.把一张矩形纸片沿着它的两条对称轴对折后成如图所示的图形,然后沿虚线剪下图①这“只角”,为了使得图①的展开图有一个内角为的菱形,若,则 .
11.如图,在中,,若点P在边上,且,,则 cm.
三、计算题
12.如图,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若DE=1,求DF的长.
13.如图,在平面直角坐标系中,,是矩形的两个顶点,双曲线经过的中点,点是矩形与双曲线的另一个交点.
(1)点的坐标为 ,点的坐标为 ;
(2)动点在第一象限内,且满足;
若点在这个反比例函数的图象上,求点的坐标;
若点是平面内一点,使得以为顶点的四边形是菱形,请你直接写出满足条件的所有点的坐标.
四、解答题
14.如图所示,平行四边形ABCD中,E、F是对角线BD上两点,连接AE、AF、CE、CF,添加一个什么条件,可使四边形AECF是平行四边形?并给出证明.
五、作图题
15.下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:如图1,直线l 及直线l 外一点A.
求作:直线AD,使得AD// l.
作法:如图2,
①在直线l 上任取两点B,C,连接AB;
②分别以点A,C 为圆心,线段BC,AB 长为半径画弧,两弧在直线l 上方相交于点D;
③作直线AD.
直线AD 就是所求作的直线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接CD.
∵ AB =▲,BC =▲,
∴ 四边形ABCD 为平行四边形( )(填推理的依据).
∴ AD// l.
六、综合题
16.如图,在梯形ABCD中,AB∥CD.
(1)已知∠A=∠B,求证:AD=BC;
(2)已知AD=BC,求证:∠A=∠B.
17.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.
(1)求证:AE=BF;
(2)若点E恰好是AD的中点,AB=2,求BD的值.
18.如图,某型号千斤顶的工作原理是利用四边形的不稳定性,图中的菱形是该型号千斤顶的示意图,保持菱形边长不变,可通过改变的长来调节的长.已知,的初始长为,如果要使的长达到,那么的长需要缩短多少.
答案解析部分
1.【答案】D
【知识点】菱形的性质;矩形的性质
2.【答案】C
【知识点】平行线的性质;菱形的性质
3.【答案】B
【知识点】平行四边形的性质;平行四边形的判定与性质
4.【答案】B
【知识点】菱形的性质
5.【答案】B
【知识点】平行四边形的判定与性质
6.【答案】14
【知识点】菱形的性质
7.【答案】40
【知识点】勾股定理;菱形的性质
8.【答案】
【知识点】菱形的性质;翻折变换(折叠问题)
9.【答案】12
【知识点】菱形的性质
10.【答案】
【知识点】菱形的性质
11.【答案】10
【知识点】等腰三角形的判定;平行四边形的判定与性质
12.【答案】解:∵D、E分别是边、的中点
∴ ∥
∵
∴
∵∥
∴四边形为平行四边形
∴
∴.
【知识点】平行四边形的判定与性质
13.【答案】(1),;
(2);或或或.
【知识点】勾股定理;菱形的性质;矩形的性质
14.【答案】可添加BE=DF(或AE=CF等).
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵BE=DF,
∴△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴∠AEF=CFE,
∴AE∥CF,
∴四边形AECF是平行四边形 (其他证方法:连对角线等 )
【知识点】全等三角形的判定与性质;平行四边形的判定与性质
15.【答案】(1)解:如图所示,
(2)证明:连接CD.
∵ AB =CD,BC =AD,
∴ 四边形ABCD 为平行四边形(两组对边分别相等的四边形是平行四边形)(填推理的依据).
∴ AD// l.
故答案为:,,两组对边分别相等的四边形是平行四边形.
【知识点】平行四边形的判定与性质;作图-平行线
16.【答案】(1)解:如图,过点C作CE∥DA,交AB于点E
∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵CE∥DA
∴∠A=∠CEB
又∵∠A=∠B
∴∠CEB=∠B
∴EC=BC
∴AD=BC
(2)解:∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵AD=BC
∴EC=BC
∴∠CEB=∠B
又∵CE∥DA
∴∠CEB=∠A
∴∠B=∠A
【知识点】等式的基本性质;等腰三角形的性质;平行四边形的判定与性质
17.【答案】(1)证明:四边形ABCD是菱形
∴AB=BC,AD∥BC
∴∠A=∠CBF
∵BE⊥AD、CF⊥AB
∴∠AEB=∠BFC=90°
∴△AEB≌△BFC(AAS)
∴AE=BF
(2)解:∵E是AD中点,且BE⊥AD
∴直线BE为AD的垂直平分线
∴BD=AB=2
【知识点】线段垂直平分线的性质;菱形的性质
18.【答案】的长需要缩短
【知识点】勾股定理;菱形的性质
21世纪教育网(www.21cnjy.com)
1 / 9
