第9章 矩形·菱形与正方形(含答案)
文档属性
| 名称 | 第9章 矩形·菱形与正方形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 919.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-28 17:59:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第9章 矩形·菱形与正方形
一、单选题
1.下列命题中,假命题是( )
A.平行四边形的对角线互相垂直平分
B.矩形的对角线相等
C.菱形的面积等于两条对角线乘积的一半
D.对角线相等的菱形是正方形
2.正方形具有而矩形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对边平行且相等 D.对角线互相垂直平分
3.如图,有一块菱形纸片 ,沿高 剪下后拼成一个矩形,若矩形相邻两边 和 的长分别是5和3,则 的长是( )
A. B.1 C.2 D.
4.如图,已知四边形是平行四边形,下列结论中正确的是( )
A.当 时,它是菱形 B.当时,它是矩形
C.当时,它是菱形 D.当时,它是正方形
5.在菱形中,已知对角线,的长度分别为,,则菱形的边长为( )
A. B. C. D.
6.如图,菱形ABCD中,AC=6,BD=8,AH⊥BC于点H.则AH=( )
A.24 B.10 C. D.
7.如图,四边形的四个顶点分别在矩形的边和对角线上,已知,下列条件能使四边形是平行四边形的是( )
A. B. C. D.
8.菱形具有,但矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对边平行且相等 D.对角线互相垂直
9.如图在边长为1的小正方形构成的5×4的网格中,定义:以网格中的格点为顶点的正方形叫做格点正方形.则图中完全包含“”的格点正方形最多能画( )
A.13个 B.16个 C.19个 D.21个
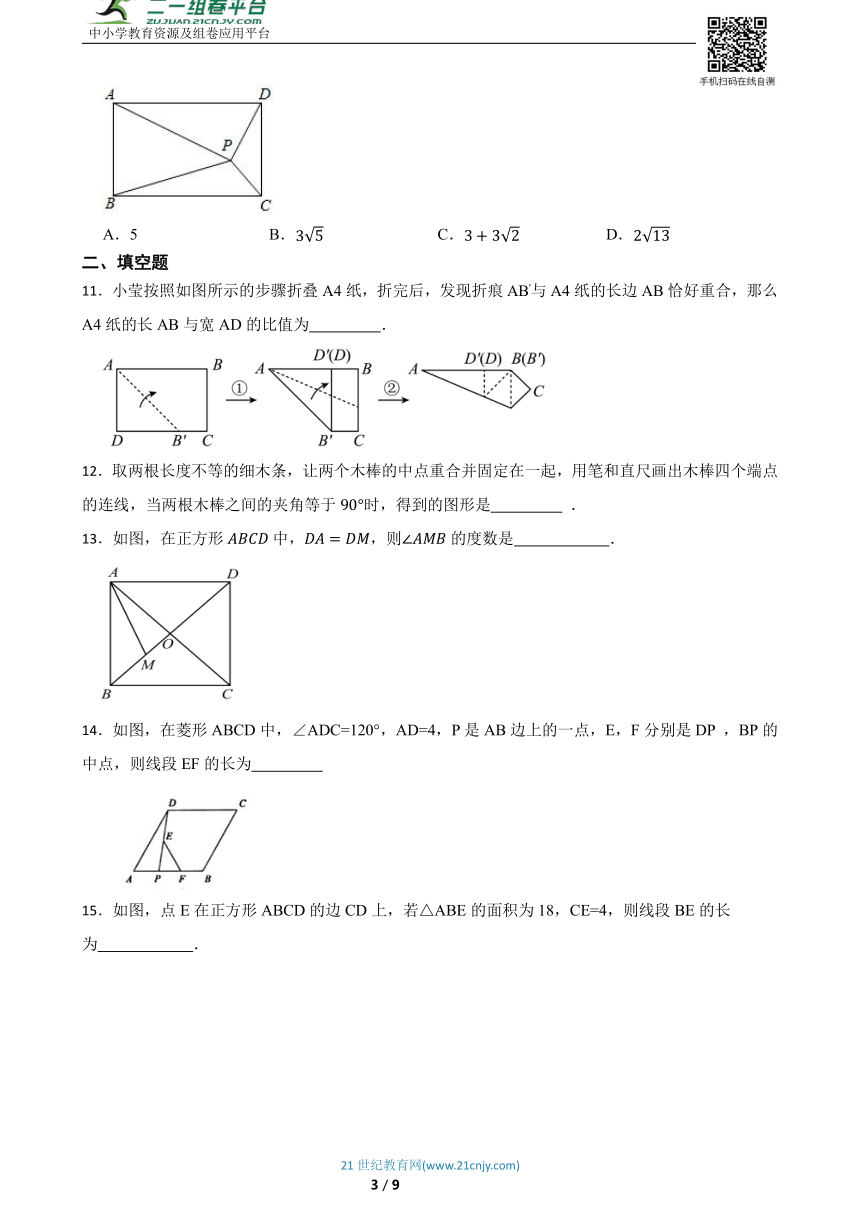
10.如图,在矩形ABCD中,AB=3,BC=4,在矩形内部有一动点P满足S△PAB=3S△PCD,则动点P到点A,B两点距离之和PA+PB的最小值为( )
A.5 B. C. D.
二、填空题
11.小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB'与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .
12.取两根长度不等的细木条,让两个木棒的中点重合并固定在一起,用笔和直尺画出木棒四个端点的连线,当两根木棒之间的夹角等于时,得到的图形是 .
13.如图,在正方形中,,则的度数是 .
14.如图,在菱形ABCD中,∠ADC=120°,AD=4,P是AB边上的一点,E,F分别是DP ,BP的中点,则线段EF的长为
15.如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为 .
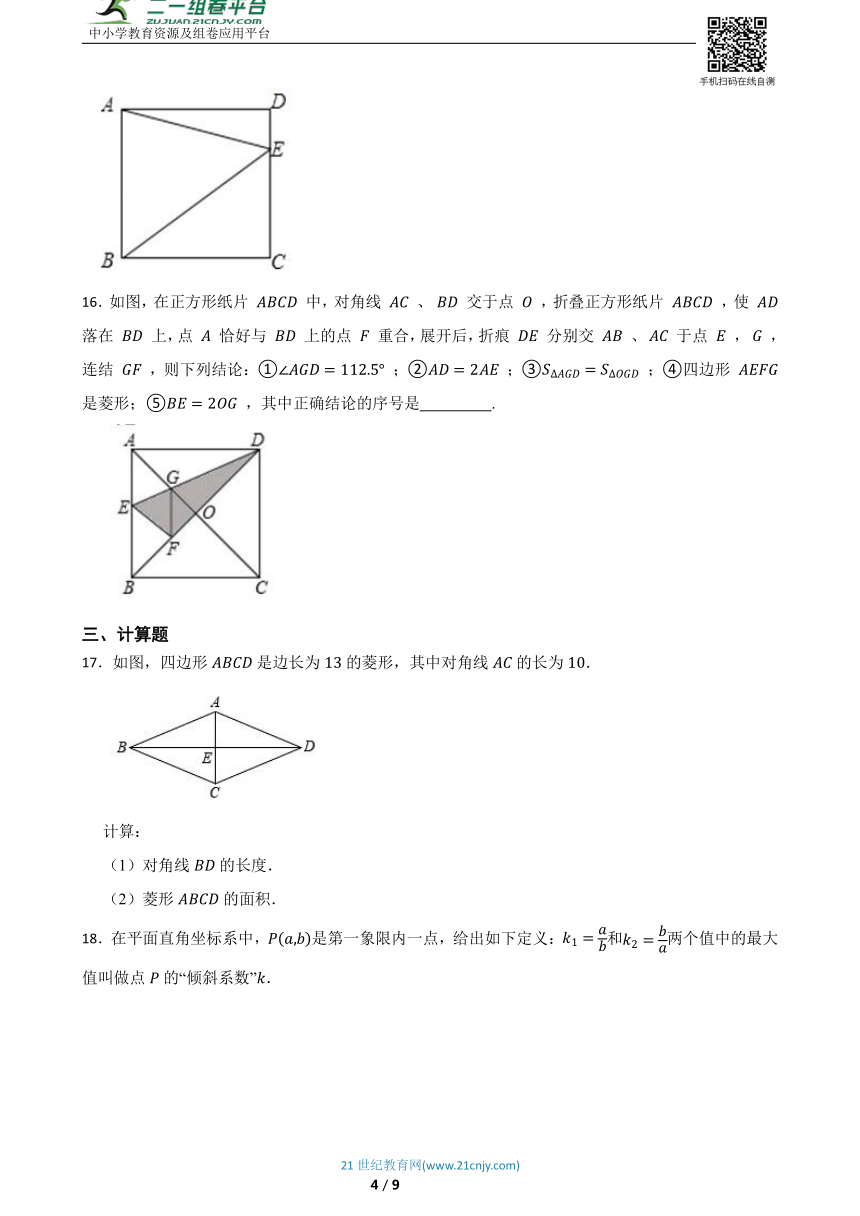
16.如图,在正方形纸片 中,对角线 、 交于点 ,折叠正方形纸片 ,使 落在 上,点 恰好与 上的点 重合,展开后,折痕 分别交 、 于点 , ,连结 ,则下列结论:① ;② ;③ ;④四边形 是菱形;⑤ ,其中正确结论的序号是 .
三、计算题
17.如图,四边形是边长为的菱形,其中对角线的长为.
计算:
(1)对角线的长度.
(2)菱形的面积.
18.在平面直角坐标系中,是第一象限内一点,给出如下定义:和两个值中的最大值叫做点的“倾斜系数”.
(1)求点的“倾斜系数”的值;
(2)已知点的“倾斜系数”,且,求的长;
(3)如图,边长为的正方形在第一象限内,对角线在直线上,对于正方形边上任意一点都有“倾斜系数”,则实数的取值范围是______.
19.如图,在平面直角坐标系中,直线与x轴、y轴分别交于点D、C,直线与y轴交于点,与直线交于点.
(1)求直线的解析式;
(2)点E是射线上一动点,过点E作轴,交直线于点F.若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;
(3)设P是射线上一点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
四、解答题
20.菱形的两条对角线相交于点O.已知,,求菱形的两条对角线的长及它的面积.
21.如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A﹣B﹣C﹣D回到点A,设点P运动的时间为t秒.
(1)当t=3秒时,求△ABP的面积;
(2)当t为何值时,点P与点A的距离为5cm?
(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边.
22.如图,在正方形ABCD中,EF分别是BC,CD上的点,且∠EAF=45°,探究线段BE,FD与EF之间的数量关系.某同学探究的方法大致是将△ABE绕A点旋转90°使得B与D重合,连接AG,由此得到AE=AG,BE=GD,证明∠EAF=∠GAF=45°,再证△EAF≌△GAF,最后通过转化可得出结论:EF=BE+FD.请帮该同学写出证明过程.
23.已知:如图①,在矩形ABCD中,AB=3,AD=4,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AF和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A'BF',在旋转过程中,设A'F'所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】平行四边形的性质;菱形的性质;矩形的性质;正方形的性质;真命题与假命题
2.【答案】D
【知识点】矩形的性质;正方形的性质
3.【答案】B
【知识点】勾股定理;菱形的性质
4.【答案】A
【知识点】菱形的判定;矩形的判定;正方形的判定
5.【答案】A
【知识点】勾股定理;菱形的性质
6.【答案】C
【知识点】勾股定理;菱形的性质
7.【答案】C
【知识点】平行线的性质;平行四边形的判定;矩形的性质;三角形全等的判定-SAS
8.【答案】D
【知识点】菱形的性质;矩形的性质
9.【答案】D
【知识点】勾股定理;正方形的判定
10.【答案】B
【知识点】勾股定理;矩形的性质
11.【答案】
【知识点】勾股定理;矩形的性质
12.【答案】菱形
【知识点】菱形的判定
13.【答案】
【知识点】等腰三角形的性质;正方形的性质
14.【答案】2
【知识点】菱形的性质
15.【答案】2
【知识点】勾股定理;正方形的性质
16.【答案】①④⑤
【知识点】平行线的性质;菱形的判定;正方形的性质;翻折变换(折叠问题)
17.【答案】(1);
(2)
【知识点】勾股定理;菱形的性质
18.【答案】(1)
(2)
(3)
【知识点】解分式方程;勾股定理;正方形的性质
19.【答案】(1)
(2)或
(3)或或
【知识点】待定系数法求一次函数解析式;平行四边形的性质;菱形的判定与性质;正方形的判定与性质
20.【答案】,,
【知识点】勾股定理;菱形的性质
21.【答案】(1)4;(2)当秒或时,AP=5cm;(3)t=.
【知识点】勾股定理的逆定理;矩形的性质
22.【答案】证明:由旋转可知:AE=AG,BE=GD,∠BAE=∠GAD,
,
,
,
,
,
,
,
.
【知识点】正方形的性质;旋转的性质;三角形全等的判定-SAS
23.【答案】1);;(2);(3)存在,2 或 或 或
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质;平移的性质
21世纪教育网(www.21cnjy.com)
3 / 9
第9章 矩形·菱形与正方形
一、单选题
1.下列命题中,假命题是( )
A.平行四边形的对角线互相垂直平分
B.矩形的对角线相等
C.菱形的面积等于两条对角线乘积的一半
D.对角线相等的菱形是正方形
2.正方形具有而矩形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对边平行且相等 D.对角线互相垂直平分
3.如图,有一块菱形纸片 ,沿高 剪下后拼成一个矩形,若矩形相邻两边 和 的长分别是5和3,则 的长是( )
A. B.1 C.2 D.
4.如图,已知四边形是平行四边形,下列结论中正确的是( )
A.当 时,它是菱形 B.当时,它是矩形
C.当时,它是菱形 D.当时,它是正方形
5.在菱形中,已知对角线,的长度分别为,,则菱形的边长为( )
A. B. C. D.
6.如图,菱形ABCD中,AC=6,BD=8,AH⊥BC于点H.则AH=( )
A.24 B.10 C. D.
7.如图,四边形的四个顶点分别在矩形的边和对角线上,已知,下列条件能使四边形是平行四边形的是( )
A. B. C. D.
8.菱形具有,但矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线相等
C.对边平行且相等 D.对角线互相垂直
9.如图在边长为1的小正方形构成的5×4的网格中,定义:以网格中的格点为顶点的正方形叫做格点正方形.则图中完全包含“”的格点正方形最多能画( )
A.13个 B.16个 C.19个 D.21个
10.如图,在矩形ABCD中,AB=3,BC=4,在矩形内部有一动点P满足S△PAB=3S△PCD,则动点P到点A,B两点距离之和PA+PB的最小值为( )
A.5 B. C. D.
二、填空题
11.小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB'与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .
12.取两根长度不等的细木条,让两个木棒的中点重合并固定在一起,用笔和直尺画出木棒四个端点的连线,当两根木棒之间的夹角等于时,得到的图形是 .
13.如图,在正方形中,,则的度数是 .
14.如图,在菱形ABCD中,∠ADC=120°,AD=4,P是AB边上的一点,E,F分别是DP ,BP的中点,则线段EF的长为
15.如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为 .
16.如图,在正方形纸片 中,对角线 、 交于点 ,折叠正方形纸片 ,使 落在 上,点 恰好与 上的点 重合,展开后,折痕 分别交 、 于点 , ,连结 ,则下列结论:① ;② ;③ ;④四边形 是菱形;⑤ ,其中正确结论的序号是 .
三、计算题
17.如图,四边形是边长为的菱形,其中对角线的长为.
计算:
(1)对角线的长度.
(2)菱形的面积.
18.在平面直角坐标系中,是第一象限内一点,给出如下定义:和两个值中的最大值叫做点的“倾斜系数”.
(1)求点的“倾斜系数”的值;
(2)已知点的“倾斜系数”,且,求的长;
(3)如图,边长为的正方形在第一象限内,对角线在直线上,对于正方形边上任意一点都有“倾斜系数”,则实数的取值范围是______.
19.如图,在平面直角坐标系中,直线与x轴、y轴分别交于点D、C,直线与y轴交于点,与直线交于点.
(1)求直线的解析式;
(2)点E是射线上一动点,过点E作轴,交直线于点F.若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;
(3)设P是射线上一点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
四、解答题
20.菱形的两条对角线相交于点O.已知,,求菱形的两条对角线的长及它的面积.
21.如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A﹣B﹣C﹣D回到点A,设点P运动的时间为t秒.
(1)当t=3秒时,求△ABP的面积;
(2)当t为何值时,点P与点A的距离为5cm?
(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边.
22.如图,在正方形ABCD中,EF分别是BC,CD上的点,且∠EAF=45°,探究线段BE,FD与EF之间的数量关系.某同学探究的方法大致是将△ABE绕A点旋转90°使得B与D重合,连接AG,由此得到AE=AG,BE=GD,证明∠EAF=∠GAF=45°,再证△EAF≌△GAF,最后通过转化可得出结论:EF=BE+FD.请帮该同学写出证明过程.
23.已知:如图①,在矩形ABCD中,AB=3,AD=4,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AF和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A'BF',在旋转过程中,设A'F'所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】平行四边形的性质;菱形的性质;矩形的性质;正方形的性质;真命题与假命题
2.【答案】D
【知识点】矩形的性质;正方形的性质
3.【答案】B
【知识点】勾股定理;菱形的性质
4.【答案】A
【知识点】菱形的判定;矩形的判定;正方形的判定
5.【答案】A
【知识点】勾股定理;菱形的性质
6.【答案】C
【知识点】勾股定理;菱形的性质
7.【答案】C
【知识点】平行线的性质;平行四边形的判定;矩形的性质;三角形全等的判定-SAS
8.【答案】D
【知识点】菱形的性质;矩形的性质
9.【答案】D
【知识点】勾股定理;正方形的判定
10.【答案】B
【知识点】勾股定理;矩形的性质
11.【答案】
【知识点】勾股定理;矩形的性质
12.【答案】菱形
【知识点】菱形的判定
13.【答案】
【知识点】等腰三角形的性质;正方形的性质
14.【答案】2
【知识点】菱形的性质
15.【答案】2
【知识点】勾股定理;正方形的性质
16.【答案】①④⑤
【知识点】平行线的性质;菱形的判定;正方形的性质;翻折变换(折叠问题)
17.【答案】(1);
(2)
【知识点】勾股定理;菱形的性质
18.【答案】(1)
(2)
(3)
【知识点】解分式方程;勾股定理;正方形的性质
19.【答案】(1)
(2)或
(3)或或
【知识点】待定系数法求一次函数解析式;平行四边形的性质;菱形的判定与性质;正方形的判定与性质
20.【答案】,,
【知识点】勾股定理;菱形的性质
21.【答案】(1)4;(2)当秒或时,AP=5cm;(3)t=.
【知识点】勾股定理的逆定理;矩形的性质
22.【答案】证明:由旋转可知:AE=AG,BE=GD,∠BAE=∠GAD,
,
,
,
,
,
,
,
.
【知识点】正方形的性质;旋转的性质;三角形全等的判定-SAS
23.【答案】1);;(2);(3)存在,2 或 或 或
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质;平移的性质
21世纪教育网(www.21cnjy.com)
3 / 9
