20.2.2平均数,中位数和众数的选用(含答案)
文档属性
| 名称 | 20.2.2平均数,中位数和众数的选用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 217.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-28 18:06:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
20.2.2平均数,中位数和众数的应用
一、单选题
1.某鞋店试销一款女鞋,试销期间对不同颜色鞋的销售情况统计如下表:鞋店经理最关心的是哪种颜色的鞋最畅销,则对鞋店经理最有意义的统计量是 ( )
颜色
黑色
棕色
白色
红色
销售量(双)
60
50
10
15
A.平均数 B.众数 C.中位数 D.方差
2.5个整数从小到大的排列,其中位数是4,如果这组数据的唯一众数是6,则这5个整数最大的和可能是( )
A. 21 B.22 C.23 D.24
3.参加歌唱比赛的12位同学成绩各不相同,按成绩取前6位进入决赛,小颖要知道自己是否进入决赛,只需要知道这12位同学成绩的( )
A.中位数 B.众数 C.平均数 D.方差
4.甲、乙两支仪仗队队员的平均身高均为1.8米,要想知道哪支仪仗队队员的身高更为整齐,通常需要比较他们身高的( )
A.众数 B.方差 C.平均数 D.中位数
5.小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )
A.方差 B.平均数 C.众数 D.中位数
二、填空题
6.一组数据3,2,7,a,7的平均数是5,则这组数据的方差是 .
7.学校运动会上,共有15名同学参加了男子100米预赛,参赛选手要想知道自己是否能进入前8名,从而取得决赛资格,只需要了解自己的成绩以及全部成绩的 .
8.市运会举行射击比赛,校射击队从甲、乙、丙、丁四人中选拔一人参赛,在选拔赛中,每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.
甲 乙 丙 丁
平均数 8.2 8.0 8.0 8.2
方差 2.1 1.8 1.6 1.4
请你根据表中数据选一人参加比赛,最合适的人选是 .
9.某校组织35名同学参加了马拉松知识竞赛,预赛分数各不相同,取前18名同学参加决赛.其中一名同学知道自己的分数后,要判断自己能否进入决赛,只需要知道这35名同学分数的 .(填“众数”,“中位数”,“平均数”,“方差”)
10.要反映我县某一周每天的最高气温的变化趋势,宜采用 .(从①条形统计图 ②扇形统计图 ③频数分布直方图 ④折线统计图中选择答案,只填序号即可)
11.极差、 、 都是用来描述一组数据的 情况的特征数据.
三、计算题
12.每年6月5日是世界环境日,为增强学生的环境保护意识,某学校举行了“环保主题知识竞赛”,现从该校、两个班级中各抽取10名学生的竞赛成绩(成绩均为整数,满分10分)进行整理、描述和分析,下面给出了部分信息:
班10名学生的成绩为:7,8,8,8,8,9,9,9,10,10.
、两个班级抽取学生测试成绩统计表
统计量 班 班
平均数 8.6 8.6
中位数 9
众数 8
班抽取学生测试成绩条形统计图
根据以上信息,解答下列问题:
(1)直接写出上述表中的,的值;
(2)根据以上数据,你认为、两个班级中哪个班环保知识掌握得更好?请说明理由.(写出一条即可)
(3)如果将平均数、中位数、众数依次按50%、30%、20%的权重计算、两个班的成绩,哪个班的成绩高?
四、解答题
13. 数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动。同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长(单位:,宽(单位:的数据后,分别计算长宽比,整理数据如下:
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
分析数据如下:
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 4.0 0.0424
荔枝树叶的长宽比 1.95 0.0669
【问题解决】
(1)m= ,n= ,并求荔枝树叶的长宽比的平均数.
(2)同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”
同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”以上两位同学的说法中,合理的是 同学;
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.
五、综合题
14.某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数 6 7 8 9
人数 1 5 2
(1)填空:10名学生的射击成绩的众数是 ,中位数是 .
(2)这10名学生的平均成绩为 .
(3)若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有 是优秀射手.
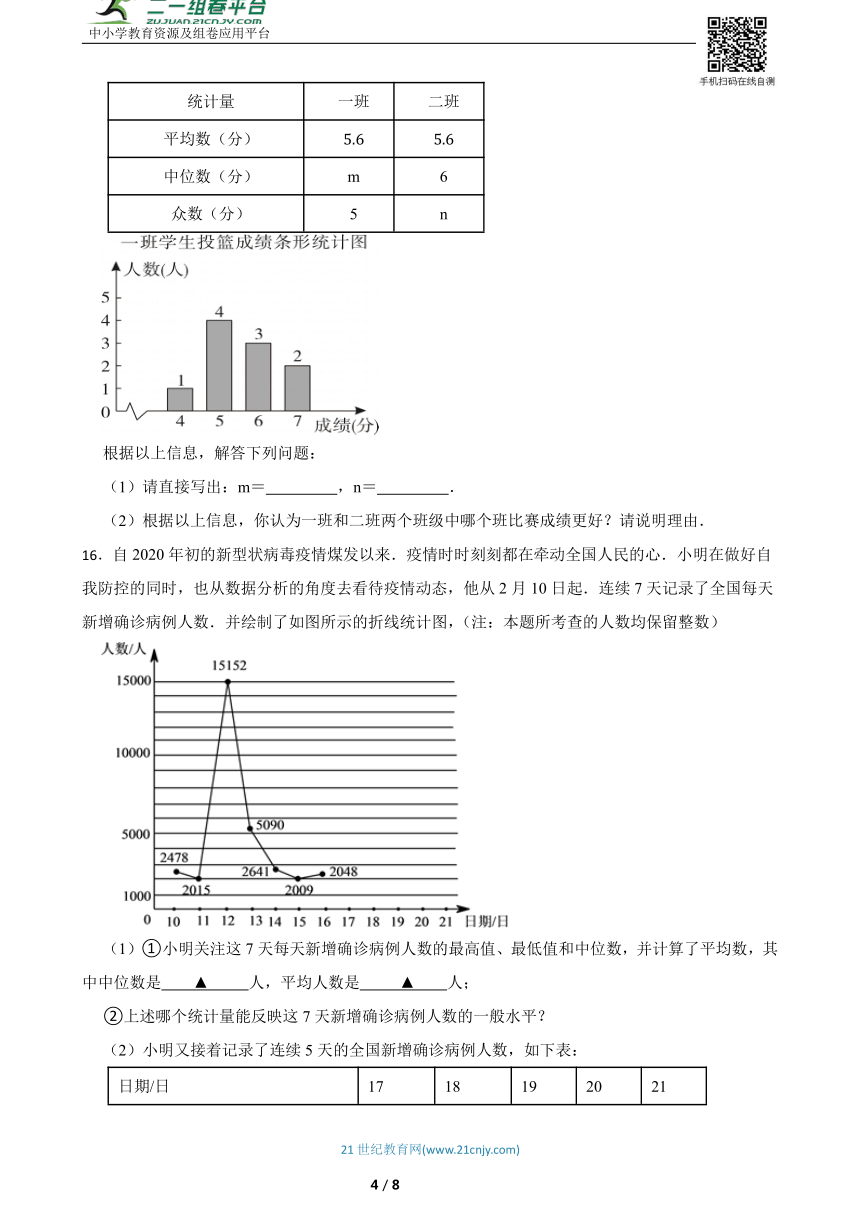
15.某校组织八年级篮球投篮赛,在一班和二班两个班级中各随机抽取10名学生的投篮成绩进行整理、描述和分析,得出下面部分信息:二班10名学生的成绩分别为(单位:分):4,4,4,5,6,6,6,6,7,8.
一班、二班学生投篮成绩统计表
统计量 一班 二班
平均数(分)
中位数(分) m 6
众数(分) 5 n
根据以上信息,解答下列问题:
(1)请直接写出:m= ,n= .
(2)根据以上信息,你认为一班和二班两个班级中哪个班比赛成绩更好?请说明理由.
16.自2020年初的新型状病毒疫情煤发以来.疫情时时刻刻都在牵动全国人民的心.小明在做好自我防控的同时,也从数据分析的角度去看待疫情动态,他从2月10日起.连续7天记录了全国每天新增确诊病例人数.并绘制了如图所示的折线统计图,(注:本题所考查的人数均保留整数)
(1)①小明关注这7天每天新增确诊病例人数的最高值、最低值和中位数,并计算了平均数,其中中位数是 ▲ 人,平均人数是 ▲ 人;
②上述哪个统计量能反映这7天新增确诊病例人数的一般水平?
(2)小明又接着记录了连续5天的全国新增确诊病例人数,如下表:
日期/日 17 18 19 20 21
新增确诊病例人数/人 1886 1749 820 889 397
①请在图12中补画出这5天每天新增确诊病例人数的折线统计图;
②求2月10日至2月21日每天新增确诊病例人数的中位数.
(3)请你分别通过对上述两个中位数的比较和全部折线图来说明每天新增确诊病例人数的升降趋势
六、实践探究题
17. “防溺水”是校园安全教育工作重点之一.某校为确保学生安全,开展了“远离溺水 珍爱生命”的防溺水安全知识竞赛.现从七年级、八年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
七年级:92,75,82,96,84,90,85,97,85,92,68,100,85,86,95,85,89,90,91,93.
八年级:90,87,93,97,90,84,92,72,100,80,90,91,59,93,87,90,82,91,92,100.
【整理与分析数据】
50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七年级 0 1 1 8 a
八年级 1 0 1 5 13
【应用数据】
平均数 众数 中位数
七年级 88 85 b
八年级 88 c 90
(1)由上表填空:a= ,b= ,c= ;
(2)若成绩不低于90分为优秀等次,该校七、八年级共有学生1600人,请你估计两个年级在本次竞赛中获得优秀等次的共有多少人?
(3)你认为哪个年级的学生对防溺水安全知识掌握的总体水平较好,请从两个不同的角度说明理由.
答案解析部分
1.【答案】B
【知识点】常用统计量的选择
2.【答案】A
【知识点】分析数据的集中趋势(平均数、中位数、众数)
3.【答案】A
【知识点】常用统计量的选择
4.【答案】B
【知识点】常用统计量的选择
5.【答案】D
【知识点】分析数据的集中趋势(平均数、中位数、众数)
6.【答案】4.4
【知识点】分析数据的集中趋势(平均数、中位数、众数)
7.【答案】中位数
【知识点】常用统计量的选择
8.【答案】丁
【知识点】常用统计量的选择
9.【答案】中位数
【知识点】中位数;常用统计量的选择
10.【答案】④
【知识点】折线统计图;常用统计量的选择
11.【答案】方差;标准差;波动
【知识点】常用统计量的选择
12.【答案】(1)a=10,b=8.5;(2)A班学生环保知识掌握得更好,理由:A班和B班学生的平均分相同,A班的中位数和众数都高于B班;(3)A班的成绩高.
【知识点】统计表;中位数;常用统计量的选择;众数
13.【答案】(1)3.75;2.0
(2)B
(3)解:树叶来自荔枝树;理由:根据长与宽的比值大约为2可得
【知识点】中位数;分析数据的集中趋势(平均数、中位数、众数);众数
14.【答案】(1)7环;7环
(2)7.5环
(3)100人
【知识点】分析数据的集中趋势(平均数、中位数、众数)
15.【答案】(1)5.5;6
(2)解:二班的比赛成绩更好,
由于两个班抽取的学生成绩中平均数相等,二班的中位数和众数都比一班高,
说明二班的总体成绩比一班高,故二班的比赛成绩更好.
【知识点】中位数;分析数据的集中趋势(平均数、中位数、众数);众数
16.【答案】(1)2478;4490;解:②由中位数的性质不受个别较大数据的影响,而且处于中间位置,前面与后面的均相等,处于中间水平,为此选取中位数
(2)解:①由折线图表示每日的新增人数的具体数目,在图中描出一下5点(17,1886),(18,1749),(19,820),(20,889),(21,397),再连线,补全折线统计图如图所示:
②把给的数据从大到小进行排列15152,5000,2641, 2478, 2018, 2015, 2000, 1886, 1749, 889, 820,397,一共12个数据,第六第七两个数据的平均数为中位数,所求的中位数为 (人).
(3)解:通过对两个中位数第一次是2478,第二次2012的比较可以看出,12天每天新增确诊病例人数的中位数小于前7天每天新增确诊病例人数的中位数.说明每天新增确诊病例人数呈下降趋势:通过补画完的折线图可以看出,每天新增确诊病例人数呈减少趋势,说明每天新增确诊病例人数呈下降趋势
【知识点】利用统计图表描述数据;平均数及其计算;中位数;常用统计量的选择
17.【答案】(1)10;;90
(2)解:(人),
答:估计两个年级在本次竞赛中获得优秀等次的共有920人.
(3)解:八年级的学生对防溺水安全知识掌握的总体水平较好.
理由:七、八年级的平均分相等;八年级成绩的众数为90,高于七年级学生成绩的众数85;八年级成绩的中位数为90,高于七年级学生成绩的中位数,综合比较,八年级的学生对防溺水安全知识掌握的总体水平较好.
【知识点】频数(率)分布表;中位数;分析数据的集中趋势(平均数、中位数、众数);众数
21世纪教育网(www.21cnjy.com)
1 / 8
20.2.2平均数,中位数和众数的应用
一、单选题
1.某鞋店试销一款女鞋,试销期间对不同颜色鞋的销售情况统计如下表:鞋店经理最关心的是哪种颜色的鞋最畅销,则对鞋店经理最有意义的统计量是 ( )
颜色
黑色
棕色
白色
红色
销售量(双)
60
50
10
15
A.平均数 B.众数 C.中位数 D.方差
2.5个整数从小到大的排列,其中位数是4,如果这组数据的唯一众数是6,则这5个整数最大的和可能是( )
A. 21 B.22 C.23 D.24
3.参加歌唱比赛的12位同学成绩各不相同,按成绩取前6位进入决赛,小颖要知道自己是否进入决赛,只需要知道这12位同学成绩的( )
A.中位数 B.众数 C.平均数 D.方差
4.甲、乙两支仪仗队队员的平均身高均为1.8米,要想知道哪支仪仗队队员的身高更为整齐,通常需要比较他们身高的( )
A.众数 B.方差 C.平均数 D.中位数
5.小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )
A.方差 B.平均数 C.众数 D.中位数
二、填空题
6.一组数据3,2,7,a,7的平均数是5,则这组数据的方差是 .
7.学校运动会上,共有15名同学参加了男子100米预赛,参赛选手要想知道自己是否能进入前8名,从而取得决赛资格,只需要了解自己的成绩以及全部成绩的 .
8.市运会举行射击比赛,校射击队从甲、乙、丙、丁四人中选拔一人参赛,在选拔赛中,每人射击10次,计算他们10发成绩的平均数(环)及方差如下表.
甲 乙 丙 丁
平均数 8.2 8.0 8.0 8.2
方差 2.1 1.8 1.6 1.4
请你根据表中数据选一人参加比赛,最合适的人选是 .
9.某校组织35名同学参加了马拉松知识竞赛,预赛分数各不相同,取前18名同学参加决赛.其中一名同学知道自己的分数后,要判断自己能否进入决赛,只需要知道这35名同学分数的 .(填“众数”,“中位数”,“平均数”,“方差”)
10.要反映我县某一周每天的最高气温的变化趋势,宜采用 .(从①条形统计图 ②扇形统计图 ③频数分布直方图 ④折线统计图中选择答案,只填序号即可)
11.极差、 、 都是用来描述一组数据的 情况的特征数据.
三、计算题
12.每年6月5日是世界环境日,为增强学生的环境保护意识,某学校举行了“环保主题知识竞赛”,现从该校、两个班级中各抽取10名学生的竞赛成绩(成绩均为整数,满分10分)进行整理、描述和分析,下面给出了部分信息:
班10名学生的成绩为:7,8,8,8,8,9,9,9,10,10.
、两个班级抽取学生测试成绩统计表
统计量 班 班
平均数 8.6 8.6
中位数 9
众数 8
班抽取学生测试成绩条形统计图
根据以上信息,解答下列问题:
(1)直接写出上述表中的,的值;
(2)根据以上数据,你认为、两个班级中哪个班环保知识掌握得更好?请说明理由.(写出一条即可)
(3)如果将平均数、中位数、众数依次按50%、30%、20%的权重计算、两个班的成绩,哪个班的成绩高?
四、解答题
13. 数学活动课上,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动。同学们随机收集芒果树、荔枝树的树叶各10片,通过测量得到这些树叶的长(单位:,宽(单位:的数据后,分别计算长宽比,整理数据如下:
1 2 3 4 5 6 7 8 9 10
芒果树叶的长宽比 3.8 3.7 3.5 3.4 3.8 4.0 3.6 4.0 3.6 4.0
荔枝树叶的长宽比 2.0 2.0 2.0 2.4 1.8 1.9 1.8 2.0 1.3 1.9
分析数据如下:
平均数 中位数 众数 方差
芒果树叶的长宽比 3.74 4.0 0.0424
荔枝树叶的长宽比 1.95 0.0669
【问题解决】
(1)m= ,n= ,并求荔枝树叶的长宽比的平均数.
(2)同学说:“从树叶的长宽比的方差来看,我认为芒果树叶的形状差别大.”
同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现荔枝树叶的长约为宽的两倍.”以上两位同学的说法中,合理的是 同学;
(3)现有一片长,宽的树叶,请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.
五、综合题
14.某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数 6 7 8 9
人数 1 5 2
(1)填空:10名学生的射击成绩的众数是 ,中位数是 .
(2)这10名学生的平均成绩为 .
(3)若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有 是优秀射手.
15.某校组织八年级篮球投篮赛,在一班和二班两个班级中各随机抽取10名学生的投篮成绩进行整理、描述和分析,得出下面部分信息:二班10名学生的成绩分别为(单位:分):4,4,4,5,6,6,6,6,7,8.
一班、二班学生投篮成绩统计表
统计量 一班 二班
平均数(分)
中位数(分) m 6
众数(分) 5 n
根据以上信息,解答下列问题:
(1)请直接写出:m= ,n= .
(2)根据以上信息,你认为一班和二班两个班级中哪个班比赛成绩更好?请说明理由.
16.自2020年初的新型状病毒疫情煤发以来.疫情时时刻刻都在牵动全国人民的心.小明在做好自我防控的同时,也从数据分析的角度去看待疫情动态,他从2月10日起.连续7天记录了全国每天新增确诊病例人数.并绘制了如图所示的折线统计图,(注:本题所考查的人数均保留整数)
(1)①小明关注这7天每天新增确诊病例人数的最高值、最低值和中位数,并计算了平均数,其中中位数是 ▲ 人,平均人数是 ▲ 人;
②上述哪个统计量能反映这7天新增确诊病例人数的一般水平?
(2)小明又接着记录了连续5天的全国新增确诊病例人数,如下表:
日期/日 17 18 19 20 21
新增确诊病例人数/人 1886 1749 820 889 397
①请在图12中补画出这5天每天新增确诊病例人数的折线统计图;
②求2月10日至2月21日每天新增确诊病例人数的中位数.
(3)请你分别通过对上述两个中位数的比较和全部折线图来说明每天新增确诊病例人数的升降趋势
六、实践探究题
17. “防溺水”是校园安全教育工作重点之一.某校为确保学生安全,开展了“远离溺水 珍爱生命”的防溺水安全知识竞赛.现从七年级、八年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
七年级:92,75,82,96,84,90,85,97,85,92,68,100,85,86,95,85,89,90,91,93.
八年级:90,87,93,97,90,84,92,72,100,80,90,91,59,93,87,90,82,91,92,100.
【整理与分析数据】
50≤x≤59 60≤x≤69 70≤x≤79 80≤x≤89 90≤x≤100
七年级 0 1 1 8 a
八年级 1 0 1 5 13
【应用数据】
平均数 众数 中位数
七年级 88 85 b
八年级 88 c 90
(1)由上表填空:a= ,b= ,c= ;
(2)若成绩不低于90分为优秀等次,该校七、八年级共有学生1600人,请你估计两个年级在本次竞赛中获得优秀等次的共有多少人?
(3)你认为哪个年级的学生对防溺水安全知识掌握的总体水平较好,请从两个不同的角度说明理由.
答案解析部分
1.【答案】B
【知识点】常用统计量的选择
2.【答案】A
【知识点】分析数据的集中趋势(平均数、中位数、众数)
3.【答案】A
【知识点】常用统计量的选择
4.【答案】B
【知识点】常用统计量的选择
5.【答案】D
【知识点】分析数据的集中趋势(平均数、中位数、众数)
6.【答案】4.4
【知识点】分析数据的集中趋势(平均数、中位数、众数)
7.【答案】中位数
【知识点】常用统计量的选择
8.【答案】丁
【知识点】常用统计量的选择
9.【答案】中位数
【知识点】中位数;常用统计量的选择
10.【答案】④
【知识点】折线统计图;常用统计量的选择
11.【答案】方差;标准差;波动
【知识点】常用统计量的选择
12.【答案】(1)a=10,b=8.5;(2)A班学生环保知识掌握得更好,理由:A班和B班学生的平均分相同,A班的中位数和众数都高于B班;(3)A班的成绩高.
【知识点】统计表;中位数;常用统计量的选择;众数
13.【答案】(1)3.75;2.0
(2)B
(3)解:树叶来自荔枝树;理由:根据长与宽的比值大约为2可得
【知识点】中位数;分析数据的集中趋势(平均数、中位数、众数);众数
14.【答案】(1)7环;7环
(2)7.5环
(3)100人
【知识点】分析数据的集中趋势(平均数、中位数、众数)
15.【答案】(1)5.5;6
(2)解:二班的比赛成绩更好,
由于两个班抽取的学生成绩中平均数相等,二班的中位数和众数都比一班高,
说明二班的总体成绩比一班高,故二班的比赛成绩更好.
【知识点】中位数;分析数据的集中趋势(平均数、中位数、众数);众数
16.【答案】(1)2478;4490;解:②由中位数的性质不受个别较大数据的影响,而且处于中间位置,前面与后面的均相等,处于中间水平,为此选取中位数
(2)解:①由折线图表示每日的新增人数的具体数目,在图中描出一下5点(17,1886),(18,1749),(19,820),(20,889),(21,397),再连线,补全折线统计图如图所示:
②把给的数据从大到小进行排列15152,5000,2641, 2478, 2018, 2015, 2000, 1886, 1749, 889, 820,397,一共12个数据,第六第七两个数据的平均数为中位数,所求的中位数为 (人).
(3)解:通过对两个中位数第一次是2478,第二次2012的比较可以看出,12天每天新增确诊病例人数的中位数小于前7天每天新增确诊病例人数的中位数.说明每天新增确诊病例人数呈下降趋势:通过补画完的折线图可以看出,每天新增确诊病例人数呈减少趋势,说明每天新增确诊病例人数呈下降趋势
【知识点】利用统计图表描述数据;平均数及其计算;中位数;常用统计量的选择
17.【答案】(1)10;;90
(2)解:(人),
答:估计两个年级在本次竞赛中获得优秀等次的共有920人.
(3)解:八年级的学生对防溺水安全知识掌握的总体水平较好.
理由:七、八年级的平均分相等;八年级成绩的众数为90,高于七年级学生成绩的众数85;八年级成绩的中位数为90,高于七年级学生成绩的中位数,综合比较,八年级的学生对防溺水安全知识掌握的总体水平较好.
【知识点】频数(率)分布表;中位数;分析数据的集中趋势(平均数、中位数、众数);众数
21世纪教育网(www.21cnjy.com)
1 / 8
