人教版 六年级下册数学 第四单元 比例的基本性质(课件)(共50张PPT)
文档属性
| 名称 | 人教版 六年级下册数学 第四单元 比例的基本性质(课件)(共50张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-28 16:42:48 | ||
图片预览






文档简介
(共50张PPT)
比例的基本性质
两个比之间的关系(相等)。
两个数量之间的关系(相除)。
表示两个比相等的式子叫做比例。
比表示两个数相除。
比例
比
定义
区别
基本
性质
比的前项、后项同时乘或除以相同的数(0除外),比值不变。
复习导入
五星红旗——中华人民共和国的象征。
国旗之通用尺度定为如下五种,各界酌情选用:
(1)长288厘米,高192厘米。
(2)长240厘米,高160厘米。
(3)长192厘米,高128厘米。
(4)长144厘米,高96厘米。
(5)长96厘米,高64厘米。
下面是我国的国旗,求出国旗长和宽、宽和长的比值。
64 cm
96 cm
先写出比
再求比值
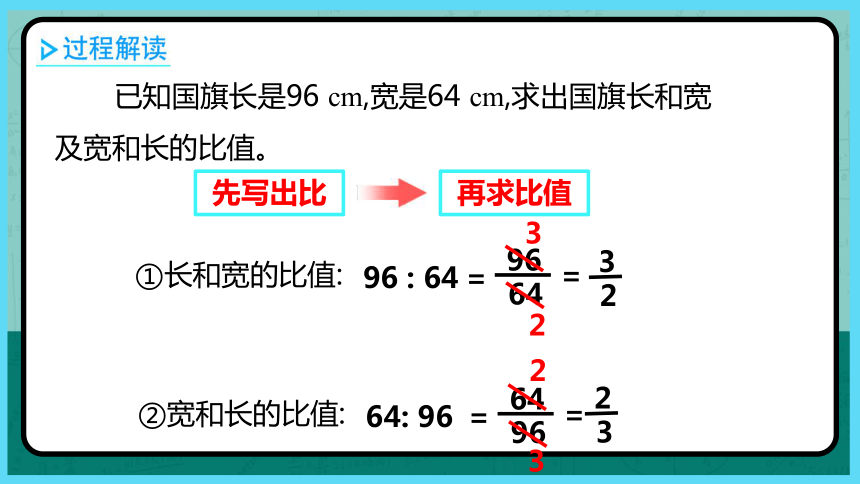
已知国旗长是96 cm,宽是64 cm,求出国旗长和宽及宽和长的比值。
①长和宽的比值:
96 : 64
=
96
64
3
2
=
②宽和长的比值:
64: 96
=
64
96
2
3
=
2
3
3
2
国旗的通用规格有五种:
①长288cm,宽192cm; ②长240cm,宽160cm;
③长192cm,宽128cm; ④长144cm,宽96cm;
⑤长96cm,宽64cm。
任选两种规格的国旗,分别求出长和宽或宽和长的比值。
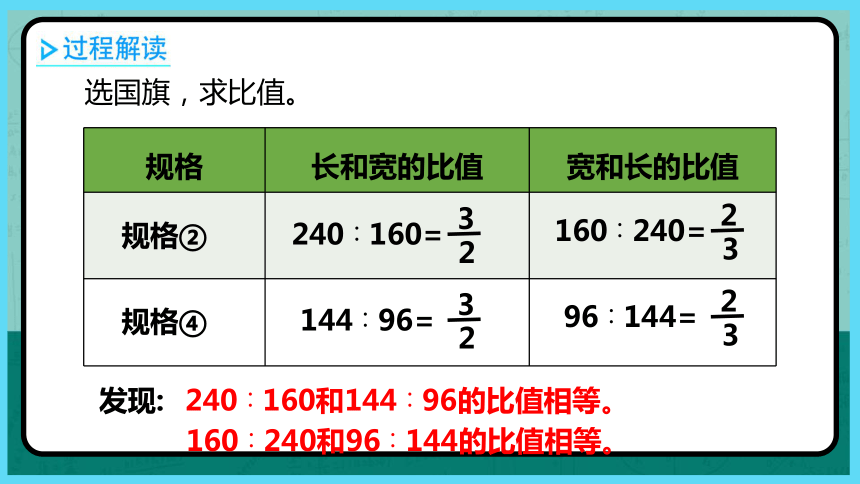
选国旗,求比值。
规格 长和宽的比值 宽和长的比值
240∶160=
3
2
规格②
160∶240=
2
3
144∶96=
3
2
规格④
96∶144=
2
3
发现:
240∶160和144∶96的比值相等。
160∶240和96∶144的比值相等。
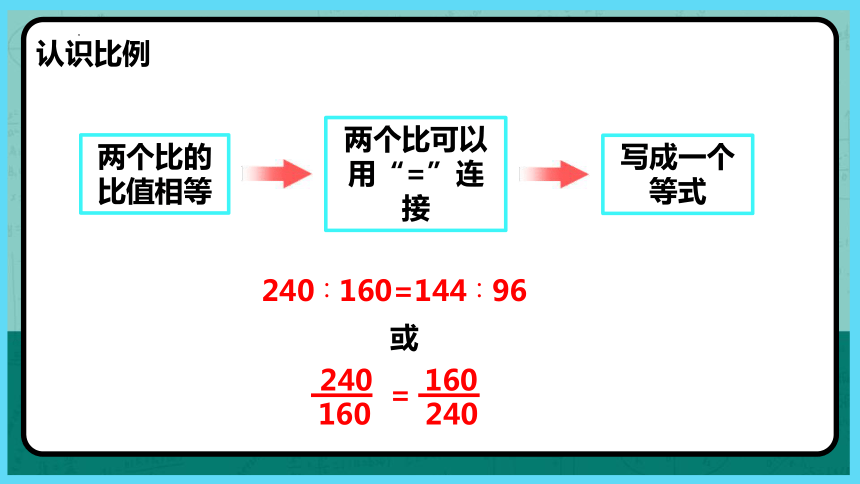
认识比例
或
240∶160=144∶96
两个比的比值相等
两个比可以用“=”连接
写成一个等式
240
160
=
160
240
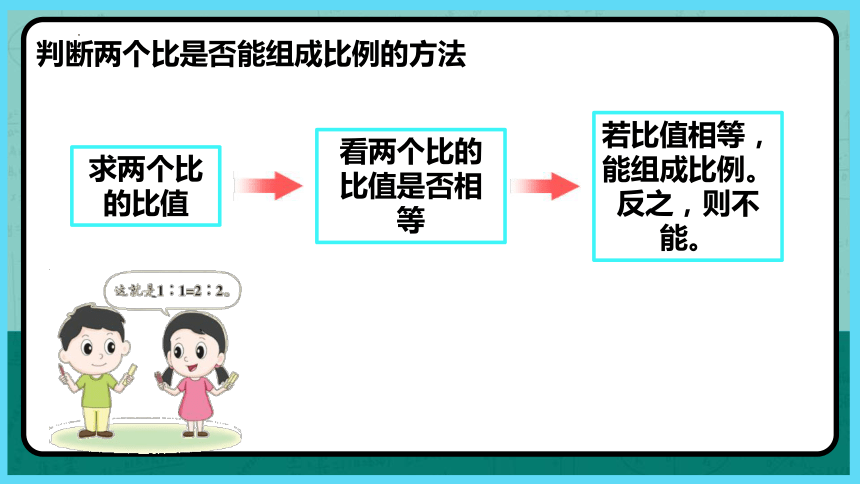
判断两个比是否能组成比例的方法
求两个比的比值
看两个比的比值是否相等
若比值相等,能组成比例。反之,则不能。
表示两个比相等的式子叫做比例。
判断两个比能不能组成比例,要看它们的比值是不是相等。
两个比的比值相等,就能组成比例。
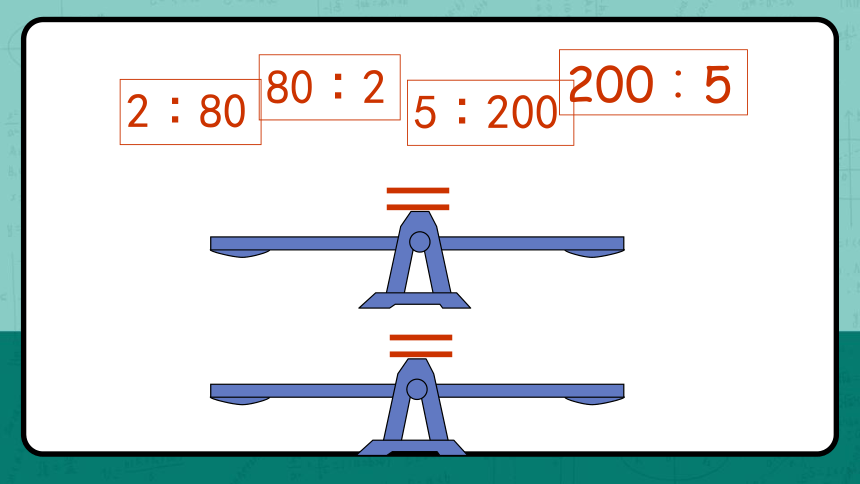
2︰80
5︰200
80︰2
200︰5
=
=
2 ︰80
5 ︰200
=
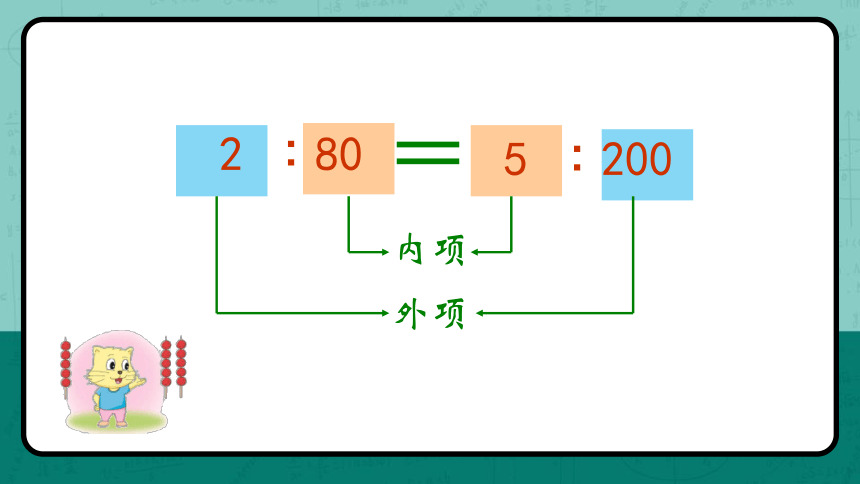
内项
外项
也可以写成
144
中间的两项叫做比例的内项。
240∶160=144∶96
240 96
两端的两项叫做比例的外项。
在比例中,组成比例的四个数叫做比例的项。
内项
外项
项
160 144
240
96
160
探究新知
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
2.4 ︰ 1.6
60︰ 40
=
外项
内项
内项积是:
1.6 × 60=96
外项积是:
2.4 × 40 = 96
2.4
40
1.6
60
×
×
=
2.4 ︰ 1.6
60 ︰ 40
=
外项
内项
=
2.4×40
1.6×60
在比例里,两个外项的积等于两个内项的积。
2.4︰1.6
60︰40
=
2.4
1.6
=
60
40
外项
外项
内项
内项
交叉相乘
=
2.4×40
1.6×60
2.4 ︰1.6
60︰40
=
外项
内项
在比例里,两个外项的积等于两个
内项的积,这叫做比例的基本性质.
比例的基本性质.
外项
240∶160=144∶96
也可以表示为
两边同时乘以 160×96,
可以得到
240×96 = 144×160
a∶b = c∶d
两边同时乘以 bd,
可以得到
内项
也可以表示为
ad= bc
(a,b,c,d都不为0)
240 96
160 144
240 96
144 160
外项
内项
a d
b c
ad
bc
23040
23040
特殊
一般
a∶b = c∶d,
也可以表示为
(a,b,c,d都不为0),
两边同时乘以 bd,
在 的等式
可以得到 。
ad= bc
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
不能组成比例。
3、2、5、6
小游戏:任意说出四个10以内的自然数,看看它们能不能组成比例。
能组成比例。
2、3、4、6
小游戏:任意说出四个10以内的自然数,看看它们能不能组成比例。
复习
判断下面每组中的两个比能否组成比例?
(1) 6:15 = 8:20
根据比例的意义判断:
根据比例的基本性质判断:
复习:
3、判断下面每组中的两个比能否组成比例?
(2) 0.5 : 0.4 = 2 : 2.5
根据比例的意义判断:
根据比例的基本性质判断:
根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?
3×40 = 20×6
根据比例的基本性质我们知道,两个内项的积等于两个外项的积。倒过来理解,乘积相等(并且不为0)的两个乘法式子,也可以改写成比例。
根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?
3×40 = 20×6
你能把上面的等式改写成比例吗?
3:20=6:40
40:20=6:3
40:6=20:3
3:6=20:40
20:3=40:6
6:3=40:20
6:40=3:20
20:40=3:6
3和40当内项
6和20当内项
判断下面哪组中的两个比可以组成比例。
(1)6∶3 和 8∶5
(2)0.2∶2.5 和 4∶50
(3) 和
(4)1.2∶ 和 ∶5
求比值
应用比例的基本性质
外项积 = 内项积
(1)6×5=30
3×8=24
24≠30
不能组成比例
(2)0.2×50=10
2.5×4=10
10=10
能组成比例
0.2∶2.5=4∶50
(3)
能组成比例
(4)1.2×5=6
不能组成比例
填一填:
24∶ = ∶2
24∶ = ∶2
24∶ = ∶2
24∶ = ∶2
24∶ = ∶2
24×2=48
6
8
8
6
3
16
16
3
1.6
30
···
已知24×3=8×9,根据比例的基本性质,你能写出比例吗 你能写几个
24×3 = 8×9
内项积
外项积
8∶24 = 3∶9
9∶24 = 3∶8
8∶3= 24∶9
9∶3 = 24∶8
24×3 = 8×9
外项积
内项积
24∶8 = 9∶3
3∶8 = 9∶24
24∶9= 8∶3
3∶9 = 8∶24
有序思考
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
a∶b = c∶d。
(a,b,c,d都不为0)。
可以得到 。
ad= bc
判断两个比是否可以组成比例
解比例
解比例。
(1)9∶2=6∶x
(2)
解:
9x=2×6
解:
x=12÷9
根据比例的基本性质,如果已知比例中的任何三项,就可以求出另外一个未知项。求比例中的未知项,叫做解比例。
分析
依据比例的基本性质,把比例式化为等积式,然后求解x。
法国巴黎的埃菲尔铁塔高度约310m。北京的世界公园里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1:10。这座模型高多少米
解:设这座模型的高度是 x m。
x∶320=1∶10
10x=320×1
x=
x=32
答:这座模型高 32 m。
依据:比例的基本性质
方法:
利用比例的基本性质将比例转化为外项之积与内项之积相等的等式
过程:
解方程
法国巴黎的埃菲尔铁塔高度约320m。北京的世界公园里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1:10。这座模型高多少米
解:设这座模型的高度是 x m。
x∶320=1∶10
10x=320×1
x=
x=32
答:这座模型高 32 m。
x∶320=1∶10
x=
x=32
方法一:
方法二:
餐馆给餐具消毒,要用100mL消毒液配成消毒水,如果消毒液与水的比是1:150,应加入水多少毫升?
解:设应加入水 x mL。
100∶x=1∶150
x=100×150
x=15000
答:应加入水 15000 毫升。
找到对应,写出比;
根据关系,组比例;
依据性质,解比例;
相同质量的水和冰的体积之比是9∶10。一块体积是 50 dm3的冰,化成水后的体积是多少
找到对应,写出比;
根据关系,组比例;
依据性质,解比例;
解:化成水后的体积是 x dm3。
9∶10 = x∶50
10x = 9×50
x = 45
相同质量的水和冰的体积之比是9∶10。一块体积是 50 dm3的冰,化成水后的体积是多少
份总关系:
50÷10×9 = 45(dm3)
分数乘法:
50× = 45(dm3)
水的体积是冰的 。
水的体积是冰的 。
分数除法:
50÷ = 45(dm3)
解:化成水后的体积是 x dm3。
9∶10 = x∶50
10x = 9×50
x = 45
答:化成水后的体积是 45 dm3。
解比例:
做一做
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
6∶3和8∶5
0.2∶2.5和4∶50
因为 6×5=30
所以 6∶3和8∶5不能组成比例.
所以 0.2∶2.5 =4∶50
10=10
3×8=24
30≠24
因为 2.5×4=10
0.2×50=10
应用比例的基本性质,判断下面哪组中的两个比
可以组成比例。
1.解比例。
解:
x=1.2÷0.3
x=4
96 ∶ 24=x ∶ 36
0.6∶x=0.3 ∶ 2
0.3x=0.6×2
解:
x=96×36÷24
x=144
24x=96×36
解:
基础练习
解:
解:
解:
2.上午10时整,在空地上直立了6根不同长度的竹竿,测得这些竹竿的高度和影子的长度如下表。
(1)写出竹竿高度与影子长度的比,并填在上表中。
竹竿高度(米) 1 2 3 4 5 6
影子长度(米) 0.5 1 1.5 2 2.5 3
竹竿高度与影长的比
1∶0.5
2 ∶ 1
3∶1.5
4 ∶ 2
5 ∶ 2.5
6 ∶ 3
(2)根据上面的结果写出三个比例。
1∶0.5=2 ∶ 1
3 ∶ 1.5=4 ∶ 2
5 ∶ 2.5=6 ∶ 3
竹竿高度(米) 1 2 3 4 5 6
影子长度(米) 0.5 1 1.5 2 2.5 3
竹竿高度与影长的比
2.上午10时整,在空地上直立了6根不同长度的竹竿,测得这些竹竿的高度和影子的长度如下表。
1∶0.5
2 ∶ 1
3∶1.5
4 ∶ 2
5 ∶ 2.5
6 ∶ 3
(3)算一算,如果竹竿的高度是3.5米,影子的长是多少米?
解:设影子的长是 x 米。
1∶0.5=3.5 ∶ x
x =3.5×0.5
x =1.75
答:影子的长是1.75米。
竹竿高度(米) 1 2 3 4 5 6
影子长度(米) 0.5 1 1.5 2 2.5 3
竹竿高度与影长的比
2.上午10时整,在空地上直立了6根不同长度的竹竿,测得这些竹竿的高度和影子的长度如下表。
1∶0.5
2 ∶ 1
3∶1.5
4 ∶ 2
5 ∶ 2.5
6 ∶ 3
(1)分别写出买两块花布花的钱数和花布的米数的比,看这两个比能不能组成比例。
25∶2=12.5
37.5 ∶ 3=12.5
可以组成比例,组成的比例为。
25 ∶ 2=37.5 ∶ 3
3.妈妈买了两块花布。
2米25元
3米37.5元
(2)如果买5米上面的花布,需要多少元钱?
解:设需要 x 元钱。
x ∶ 5=25 ∶ 2
x =125÷2
x =62.5
答:需要62.5元钱。
3.妈妈买了两块花布。
2米25元
3米37.5元
2x =25×5
(3)如果买7米下面的花布,需要多少元钱?
解:设需要 x 元钱。
x ∶ 7=37.5 ∶ 3
x =37.5×7÷3
x =87.5
答:需要87.5元钱。
3x =37.5×7
2米25元
3米37.5元
3.妈妈买了两块花布。
也可以写成
144
240∶160=144∶96
240 96
内项
外项
160 144
240
96
160
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
判断两个比是否可以组成比例
解比例
a∶b = c∶d。
(a,b,c,d都不为0)。
可以得到 。
ad= bc
表示两个比相等的式子叫做比例。
课堂小结
完成练习册本课时的习题。
课后作业
再
见
比例的基本性质
两个比之间的关系(相等)。
两个数量之间的关系(相除)。
表示两个比相等的式子叫做比例。
比表示两个数相除。
比例
比
定义
区别
基本
性质
比的前项、后项同时乘或除以相同的数(0除外),比值不变。
复习导入
五星红旗——中华人民共和国的象征。
国旗之通用尺度定为如下五种,各界酌情选用:
(1)长288厘米,高192厘米。
(2)长240厘米,高160厘米。
(3)长192厘米,高128厘米。
(4)长144厘米,高96厘米。
(5)长96厘米,高64厘米。
下面是我国的国旗,求出国旗长和宽、宽和长的比值。
64 cm
96 cm
先写出比
再求比值
已知国旗长是96 cm,宽是64 cm,求出国旗长和宽及宽和长的比值。
①长和宽的比值:
96 : 64
=
96
64
3
2
=
②宽和长的比值:
64: 96
=
64
96
2
3
=
2
3
3
2
国旗的通用规格有五种:
①长288cm,宽192cm; ②长240cm,宽160cm;
③长192cm,宽128cm; ④长144cm,宽96cm;
⑤长96cm,宽64cm。
任选两种规格的国旗,分别求出长和宽或宽和长的比值。
选国旗,求比值。
规格 长和宽的比值 宽和长的比值
240∶160=
3
2
规格②
160∶240=
2
3
144∶96=
3
2
规格④
96∶144=
2
3
发现:
240∶160和144∶96的比值相等。
160∶240和96∶144的比值相等。
认识比例
或
240∶160=144∶96
两个比的比值相等
两个比可以用“=”连接
写成一个等式
240
160
=
160
240
判断两个比是否能组成比例的方法
求两个比的比值
看两个比的比值是否相等
若比值相等,能组成比例。反之,则不能。
表示两个比相等的式子叫做比例。
判断两个比能不能组成比例,要看它们的比值是不是相等。
两个比的比值相等,就能组成比例。
2︰80
5︰200
80︰2
200︰5
=
=
2 ︰80
5 ︰200
=
内项
外项
也可以写成
144
中间的两项叫做比例的内项。
240∶160=144∶96
240 96
两端的两项叫做比例的外项。
在比例中,组成比例的四个数叫做比例的项。
内项
外项
项
160 144
240
96
160
探究新知
指出下面比例的外项和内项。
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
2.4 ︰ 1.6
60︰ 40
=
外项
内项
内项积是:
1.6 × 60=96
外项积是:
2.4 × 40 = 96
2.4
40
1.6
60
×
×
=
2.4 ︰ 1.6
60 ︰ 40
=
外项
内项
=
2.4×40
1.6×60
在比例里,两个外项的积等于两个内项的积。
2.4︰1.6
60︰40
=
2.4
1.6
=
60
40
外项
外项
内项
内项
交叉相乘
=
2.4×40
1.6×60
2.4 ︰1.6
60︰40
=
外项
内项
在比例里,两个外项的积等于两个
内项的积,这叫做比例的基本性质.
比例的基本性质.
外项
240∶160=144∶96
也可以表示为
两边同时乘以 160×96,
可以得到
240×96 = 144×160
a∶b = c∶d
两边同时乘以 bd,
可以得到
内项
也可以表示为
ad= bc
(a,b,c,d都不为0)
240 96
160 144
240 96
144 160
外项
内项
a d
b c
ad
bc
23040
23040
特殊
一般
a∶b = c∶d,
也可以表示为
(a,b,c,d都不为0),
两边同时乘以 bd,
在 的等式
可以得到 。
ad= bc
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
不能组成比例。
3、2、5、6
小游戏:任意说出四个10以内的自然数,看看它们能不能组成比例。
能组成比例。
2、3、4、6
小游戏:任意说出四个10以内的自然数,看看它们能不能组成比例。
复习
判断下面每组中的两个比能否组成比例?
(1) 6:15 = 8:20
根据比例的意义判断:
根据比例的基本性质判断:
复习:
3、判断下面每组中的两个比能否组成比例?
(2) 0.5 : 0.4 = 2 : 2.5
根据比例的意义判断:
根据比例的基本性质判断:
根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?
3×40 = 20×6
根据比例的基本性质我们知道,两个内项的积等于两个外项的积。倒过来理解,乘积相等(并且不为0)的两个乘法式子,也可以改写成比例。
根据上面的等式,你能判断哪两个是外项?哪两个是内项吗?
3×40 = 20×6
你能把上面的等式改写成比例吗?
3:20=6:40
40:20=6:3
40:6=20:3
3:6=20:40
20:3=40:6
6:3=40:20
6:40=3:20
20:40=3:6
3和40当内项
6和20当内项
判断下面哪组中的两个比可以组成比例。
(1)6∶3 和 8∶5
(2)0.2∶2.5 和 4∶50
(3) 和
(4)1.2∶ 和 ∶5
求比值
应用比例的基本性质
外项积 = 内项积
(1)6×5=30
3×8=24
24≠30
不能组成比例
(2)0.2×50=10
2.5×4=10
10=10
能组成比例
0.2∶2.5=4∶50
(3)
能组成比例
(4)1.2×5=6
不能组成比例
填一填:
24∶ = ∶2
24∶ = ∶2
24∶ = ∶2
24∶ = ∶2
24∶ = ∶2
24×2=48
6
8
8
6
3
16
16
3
1.6
30
···
已知24×3=8×9,根据比例的基本性质,你能写出比例吗 你能写几个
24×3 = 8×9
内项积
外项积
8∶24 = 3∶9
9∶24 = 3∶8
8∶3= 24∶9
9∶3 = 24∶8
24×3 = 8×9
外项积
内项积
24∶8 = 9∶3
3∶8 = 9∶24
24∶9= 8∶3
3∶9 = 8∶24
有序思考
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
a∶b = c∶d。
(a,b,c,d都不为0)。
可以得到 。
ad= bc
判断两个比是否可以组成比例
解比例
解比例。
(1)9∶2=6∶x
(2)
解:
9x=2×6
解:
x=12÷9
根据比例的基本性质,如果已知比例中的任何三项,就可以求出另外一个未知项。求比例中的未知项,叫做解比例。
分析
依据比例的基本性质,把比例式化为等积式,然后求解x。
法国巴黎的埃菲尔铁塔高度约310m。北京的世界公园里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1:10。这座模型高多少米
解:设这座模型的高度是 x m。
x∶320=1∶10
10x=320×1
x=
x=32
答:这座模型高 32 m。
依据:比例的基本性质
方法:
利用比例的基本性质将比例转化为外项之积与内项之积相等的等式
过程:
解方程
法国巴黎的埃菲尔铁塔高度约320m。北京的世界公园里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1:10。这座模型高多少米
解:设这座模型的高度是 x m。
x∶320=1∶10
10x=320×1
x=
x=32
答:这座模型高 32 m。
x∶320=1∶10
x=
x=32
方法一:
方法二:
餐馆给餐具消毒,要用100mL消毒液配成消毒水,如果消毒液与水的比是1:150,应加入水多少毫升?
解:设应加入水 x mL。
100∶x=1∶150
x=100×150
x=15000
答:应加入水 15000 毫升。
找到对应,写出比;
根据关系,组比例;
依据性质,解比例;
相同质量的水和冰的体积之比是9∶10。一块体积是 50 dm3的冰,化成水后的体积是多少
找到对应,写出比;
根据关系,组比例;
依据性质,解比例;
解:化成水后的体积是 x dm3。
9∶10 = x∶50
10x = 9×50
x = 45
相同质量的水和冰的体积之比是9∶10。一块体积是 50 dm3的冰,化成水后的体积是多少
份总关系:
50÷10×9 = 45(dm3)
分数乘法:
50× = 45(dm3)
水的体积是冰的 。
水的体积是冰的 。
分数除法:
50÷ = 45(dm3)
解:化成水后的体积是 x dm3。
9∶10 = x∶50
10x = 9×50
x = 45
答:化成水后的体积是 45 dm3。
解比例:
做一做
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
6∶3和8∶5
0.2∶2.5和4∶50
因为 6×5=30
所以 6∶3和8∶5不能组成比例.
所以 0.2∶2.5 =4∶50
10=10
3×8=24
30≠24
因为 2.5×4=10
0.2×50=10
应用比例的基本性质,判断下面哪组中的两个比
可以组成比例。
1.解比例。
解:
x=1.2÷0.3
x=4
96 ∶ 24=x ∶ 36
0.6∶x=0.3 ∶ 2
0.3x=0.6×2
解:
x=96×36÷24
x=144
24x=96×36
解:
基础练习
解:
解:
解:
2.上午10时整,在空地上直立了6根不同长度的竹竿,测得这些竹竿的高度和影子的长度如下表。
(1)写出竹竿高度与影子长度的比,并填在上表中。
竹竿高度(米) 1 2 3 4 5 6
影子长度(米) 0.5 1 1.5 2 2.5 3
竹竿高度与影长的比
1∶0.5
2 ∶ 1
3∶1.5
4 ∶ 2
5 ∶ 2.5
6 ∶ 3
(2)根据上面的结果写出三个比例。
1∶0.5=2 ∶ 1
3 ∶ 1.5=4 ∶ 2
5 ∶ 2.5=6 ∶ 3
竹竿高度(米) 1 2 3 4 5 6
影子长度(米) 0.5 1 1.5 2 2.5 3
竹竿高度与影长的比
2.上午10时整,在空地上直立了6根不同长度的竹竿,测得这些竹竿的高度和影子的长度如下表。
1∶0.5
2 ∶ 1
3∶1.5
4 ∶ 2
5 ∶ 2.5
6 ∶ 3
(3)算一算,如果竹竿的高度是3.5米,影子的长是多少米?
解:设影子的长是 x 米。
1∶0.5=3.5 ∶ x
x =3.5×0.5
x =1.75
答:影子的长是1.75米。
竹竿高度(米) 1 2 3 4 5 6
影子长度(米) 0.5 1 1.5 2 2.5 3
竹竿高度与影长的比
2.上午10时整,在空地上直立了6根不同长度的竹竿,测得这些竹竿的高度和影子的长度如下表。
1∶0.5
2 ∶ 1
3∶1.5
4 ∶ 2
5 ∶ 2.5
6 ∶ 3
(1)分别写出买两块花布花的钱数和花布的米数的比,看这两个比能不能组成比例。
25∶2=12.5
37.5 ∶ 3=12.5
可以组成比例,组成的比例为。
25 ∶ 2=37.5 ∶ 3
3.妈妈买了两块花布。
2米25元
3米37.5元
(2)如果买5米上面的花布,需要多少元钱?
解:设需要 x 元钱。
x ∶ 5=25 ∶ 2
x =125÷2
x =62.5
答:需要62.5元钱。
3.妈妈买了两块花布。
2米25元
3米37.5元
2x =25×5
(3)如果买7米下面的花布,需要多少元钱?
解:设需要 x 元钱。
x ∶ 7=37.5 ∶ 3
x =37.5×7÷3
x =87.5
答:需要87.5元钱。
3x =37.5×7
2米25元
3米37.5元
3.妈妈买了两块花布。
也可以写成
144
240∶160=144∶96
240 96
内项
外项
160 144
240
96
160
在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。
判断两个比是否可以组成比例
解比例
a∶b = c∶d。
(a,b,c,d都不为0)。
可以得到 。
ad= bc
表示两个比相等的式子叫做比例。
课堂小结
完成练习册本课时的习题。
课后作业
再
见
