直线和圆的位置关系

课件25张PPT。直线与圆的位置关系童寺镇芝溪小学 曾伟（一）教材地位与作用 直线和圆的位置关系是在学习了点和圆的位置关系的基础上进行的，为后面的圆与圆的位置关系作了铺垫．起着承上启下的作用． 直线与圆的位置关系一、教材分析直线与圆的位置关系（二）教学目标 知识目标：
理解直线和圆的三种位置关系;探究直线和圆的位置关系的数量关系及其运用。
能力目标：
渗透类比、转化、数形结合的数学思想和方法，培养学生实验、观察、猜想、概括的逻辑思维能力。
情感目标：
学生经过操作，实验，发现，归纳等数学活动，从探索直线与圆的位置关系中，体会运动变化的观点。感受数学中的美感。(三)教学重点、难点 教学重点：
理解直线和圆的三种位置关系 教学难点：
直线和圆的三种位置关系的性质与判定的应用 直线与圆的位置关系二、教法学法分析以实验探究教学法为主，整堂课紧紧围绕“情景问题——学生体验——合作交流”的模式 。激励学生积极参与、观察、发现。培养学生用创造性思维去学会学习。 直线与圆的位置关系活动一：观察图片，引入课题直线和圆的位置有
何关系？？？思考：
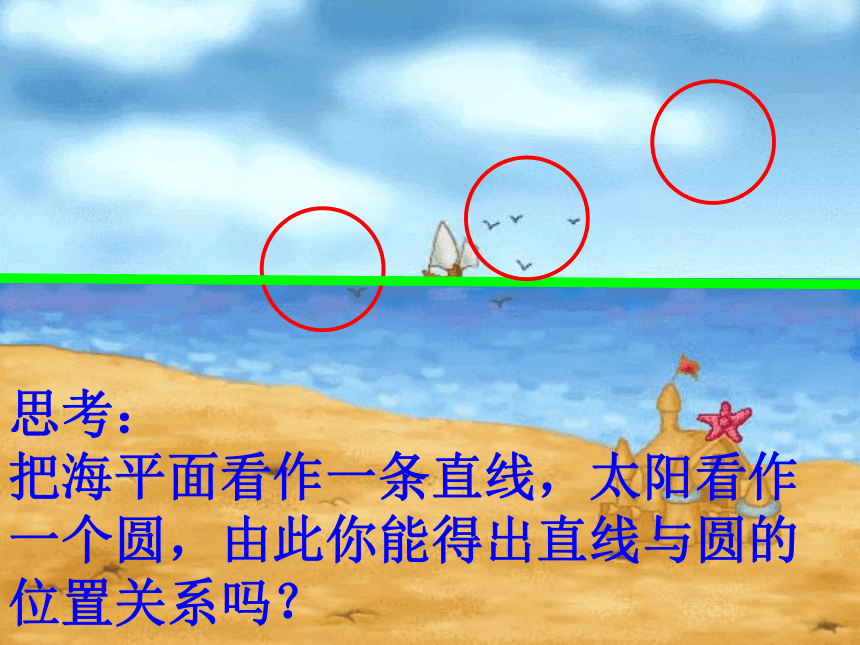
把海平面看作一条直线，太阳看作一个圆，由此你能得出直线与圆的位置关系吗？ 思考：
把海平面看作一条直线，太阳看作一个圆，由此你能得出直线与圆的位置关系吗？ 活动二：实验观察 探索新知图 1图 2图 3这条直线叫做圆的割线 ,
公共点叫直线与圆的交点。直线和圆没有公共点时,叫做直线与圆相离.直线和圆有唯一公共点时,叫做直线与圆相切.直线和圆有两个公共点时,叫做直线与圆相交. 这条直线叫做圆的切线 ,
唯一公共点叫做直线与圆的切点。1.直线与圆的位置关系（图形特征） １、直线与圆最多有两个公共点 。 （　） √×判断3 、若A是⊙O上一点， 则直线AB与⊙O相切 。( )２、若直线与圆相交，则直线上的点都在圆内。( ) 4 、若C为⊙O外的一点，则过点C的直线CD与
⊙O 相交或相离。………（ ）××生活中还有哪些例子,都给我们直线与圆的位置关系的印象.你能举出1—2个实例吗? 活动三：诱导思维、自主探究dr相离Adr相切H1、直线与圆相离2、直线与圆相切3、直线与圆相交2.直线与圆的位置关系 (数量特征).D.Ord相交
C.OB直线与圆的位置关系的性质与判定.
E. FOd>rd=rd r没有归纳小结活动四：运用新知，拓展训练 设⊙O的半径为r，圆心O到直线l的距离为d。根据下列条件判断直线l与⊙O的位置关系。试一试,我能行（2）d=1,r= ； （3）d=2,r=2； （1）d=4,r=3；∵ d ＜ r
∴直线l与⊙O相交∵d＝r
∴直线l与⊙O相切∵d＞ r
∴直线l与⊙O相离填空：1、已知⊙O的半径为5cm，点O到直线a的距离
为3cm，则⊙O与直线a的位置关系是_____;
直线a与⊙O的公共点个数是____.动动脑筋相交 相切两个3、已知⊙O的直径为10cm，点O到直线a的距离
为7cm，则⊙O与直线a的位置关系是 ____;
直线a与⊙O的公共点个数是____。零相离一个2、已知⊙O的直径是11cm，点O到直线a的距离
是5.5cm，则⊙O与直线a的位置关系是 ____;
直线a与⊙O的公共点个数是____.4、在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆
与AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm (3)r=3cm。B解后思在Rt△ABC中，∠C=90°，AC=3cm，
BC=4cm，以C为圆心，r为半径作圆。1、当 r 满足____________时，⊙C与直线AB相离。2、当 r 满足___________ 时，⊙C与直线AB相切。3、当 r 满足_________ 时，⊙C与直线AB相交。BCAD4d=2.4cm3r＜2.4cmr=2.4cmr＞2.4cm
2、对老师说你有什么困惑
1、对同学说你有什么收获
1)、知识 2)、思想方法
活动五：反思归纳 收获提升 台风是一种在沿海地区较为常见的自然灾害，它在以台风中心为圆心的数十千米乃至数百千米范围内肆虐，房屋、庄稼、汽车等将遭到极强破坏。2009年10月8日，在日本的东南方向距东京500km处有一名叫“茉莉”的台风中心形成。其中心最大风力为14级，每离开台风中心30km风力将降低一级。若此台风中心沿着北偏西150的方向以15km/h的速度移动，且台风中心风力不变。若城市所受到的台风风力为不小于4级，则称为受台风影响1、东京会受到“茉莉”台风的影响吗？2、若会受影响，那会台风将会影响东京多长时间呢？最大风力将会是几级呢？ 联系实际,拓展应用四、教学设计思路请各位评委、老师指正，谢谢！