人教版六年级上册数学3.8《分数除法的应用》 课件(共16张PPT)
文档属性
| 名称 | 人教版六年级上册数学3.8《分数除法的应用》 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-29 12:16:39 | ||
图片预览



文档简介
(共16张PPT)
分数除法的应用(4)
新课导入
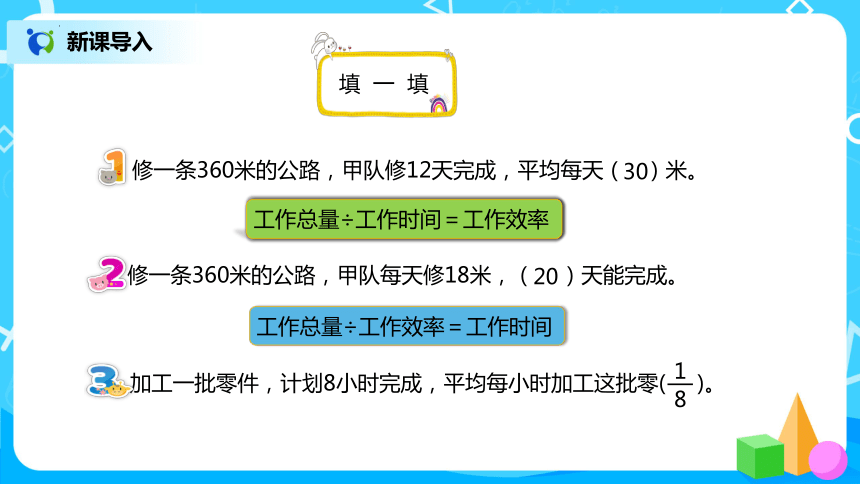
修一条360米的公路,甲队修12天完成,平均每天( )米。
30
工作总量÷工作时间=工作效率
修一条360米的公路,甲队每天修18米,( )天能完成。
20
工作总量÷工作效率=工作时间
加工一批零件,计划8小时完成,平均每小时加工这批零( )。
填 一 填
1
8
如果我们二队单独修,18天才能修完。
如果两队合修,多少天能修完?
你知道了哪些数学信息?
新课讲解
这条道路,如果我们一队单独修,12天能修完。
如果我们二队单独修,18天才能修完。
如果两队合修,多少天能修完?
工作时间
= 工作总量 ÷ 工作效率
这条路有多长呢?
新课讲解
这条道路,如果我们一队单独修,12天能修完。
如果我们二队单独修,18天才能修完。
新课讲解
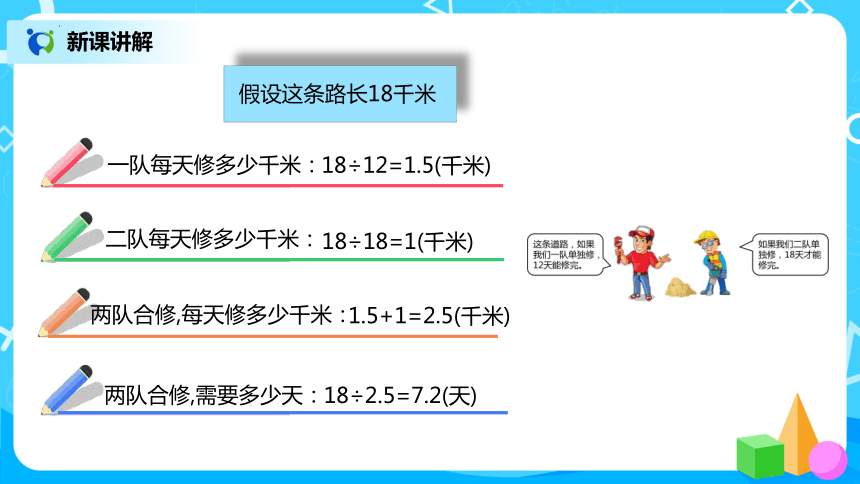
18÷2.5=7.2(天)
假设这条路长18千米
一队每天修多少千米:
18÷12=1.5(千米)
二队每天修多少千米:
18÷18=1(千米)
1.5+1=2.5(千米)
两队合修,需要多少天:
两队合修,每天修多少千米:
新课讲解
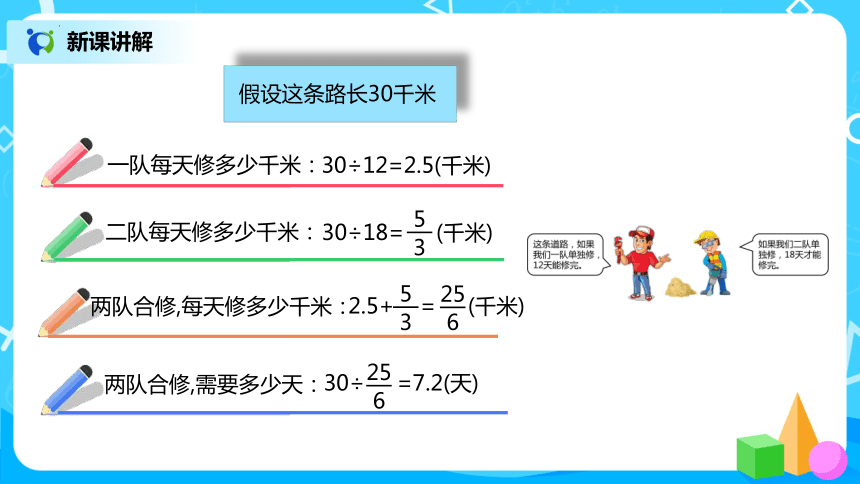
假设这条路长30千米
一队每天修多少千米:
30÷12=2.5(千米)
二队每天修多少千米:
两队合修,需要多少天:
两队合修,每天修多少千米:
30÷18= (千米)
5
3
2.5+ = (千米)
5
3
25
6
30÷ =7.2(天)
25
6
新课讲解
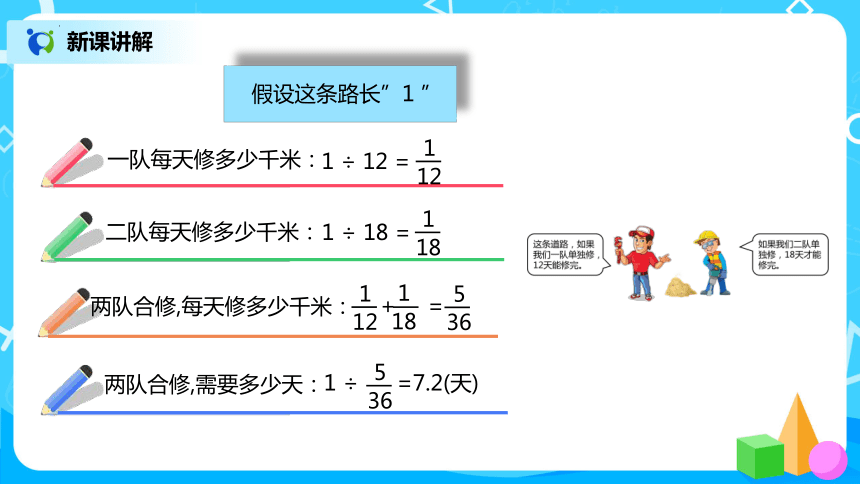
假设这条路长”1 ”
一队每天修多少千米:
二队每天修多少千米:
两队合修,需要多少天:
两队合修,每天修多少千米:
1 ÷ 18 =
1
18
1 ÷ =7.2(天)
5
36
1 ÷ 12 =
1
12
+ =
1
18
5
36
1
12
分别求出一队和二队7.2天修的道路,再将它们合起来,看一看够不够单位“1”。
×7.2+ ×7.2
1
12
1
18
= 0.6+0.4
= 1
检 验 一 下
结论正确
新课讲解
答:如果两队合修,7.2天可以修完。
= 7.2(天)
1÷(+ )
1
12
1
18
= 1÷
5
36
不管假设这条路
有多长,两队都
是7.2天修完。
通过计算你发现了什么?
新课讲解
新课讲解
以上三种解法的思维是一致的,数量关系
相同、都是用工作总量除以工作效率的和。
不管这条路假设有多长,答案都是相同的。
其中把这条路的长度设为1,计算更简便。
如果两辆车一起运,多少次能运完这批货物?
答:如果两辆车一起运,
2次能运完这批货物。
这批货物,只用我的车运,6次才能运完。
只用我的车运,3次就
能运完。
= 2(次)
1÷(+ )
1
6
1
3
= 1÷
1
2
课堂练习
加工180个零件,甲单独做要8天完成,乙单独做要12天完成。
现在甲、乙一起做,6天能完成吗?
= 4.8(天)
1÷(+ )
1
8
1
12
= 1÷
5
24
4.8 < 6
答:甲、乙一起做,6天能完成。
课堂练习
甲、乙两车从两地同时相向开出,甲车行完全程用20小时,乙车行
完全程所用的时间是甲车的 。两车出发多少小时后相遇?
3
2
30 (小时)
20 × =
3
2
= 12(小时)
1÷(+ )
1
20
1
30
= 1÷
1
12
答:两车出发12小时后相遇。
课堂练习
课堂练习
修一条公路,甲队单独修10天完成,乙队单独修15天完成。
两队一起修,多少天能完成全长的 ?
2
3
= 4(天)
2
3
÷(+ )
1
10
1
15
= ÷
1
6
2
3
答:4 天能完成全长的 ?
2
3
将工作总量看作单位“1”,
用单位时间内完成工作总量的几分之一表示工作效率。
基本等量关系式:工作总量÷工作效率之和=工作时间
获
收
我
的
课堂总结
谢谢观看
分数除法的应用(4)
新课导入
修一条360米的公路,甲队修12天完成,平均每天( )米。
30
工作总量÷工作时间=工作效率
修一条360米的公路,甲队每天修18米,( )天能完成。
20
工作总量÷工作效率=工作时间
加工一批零件,计划8小时完成,平均每小时加工这批零( )。
填 一 填
1
8
如果我们二队单独修,18天才能修完。
如果两队合修,多少天能修完?
你知道了哪些数学信息?
新课讲解
这条道路,如果我们一队单独修,12天能修完。
如果我们二队单独修,18天才能修完。
如果两队合修,多少天能修完?
工作时间
= 工作总量 ÷ 工作效率
这条路有多长呢?
新课讲解
这条道路,如果我们一队单独修,12天能修完。
如果我们二队单独修,18天才能修完。
新课讲解
18÷2.5=7.2(天)
假设这条路长18千米
一队每天修多少千米:
18÷12=1.5(千米)
二队每天修多少千米:
18÷18=1(千米)
1.5+1=2.5(千米)
两队合修,需要多少天:
两队合修,每天修多少千米:
新课讲解
假设这条路长30千米
一队每天修多少千米:
30÷12=2.5(千米)
二队每天修多少千米:
两队合修,需要多少天:
两队合修,每天修多少千米:
30÷18= (千米)
5
3
2.5+ = (千米)
5
3
25
6
30÷ =7.2(天)
25
6
新课讲解
假设这条路长”1 ”
一队每天修多少千米:
二队每天修多少千米:
两队合修,需要多少天:
两队合修,每天修多少千米:
1 ÷ 18 =
1
18
1 ÷ =7.2(天)
5
36
1 ÷ 12 =
1
12
+ =
1
18
5
36
1
12
分别求出一队和二队7.2天修的道路,再将它们合起来,看一看够不够单位“1”。
×7.2+ ×7.2
1
12
1
18
= 0.6+0.4
= 1
检 验 一 下
结论正确
新课讲解
答:如果两队合修,7.2天可以修完。
= 7.2(天)
1÷(+ )
1
12
1
18
= 1÷
5
36
不管假设这条路
有多长,两队都
是7.2天修完。
通过计算你发现了什么?
新课讲解
新课讲解
以上三种解法的思维是一致的,数量关系
相同、都是用工作总量除以工作效率的和。
不管这条路假设有多长,答案都是相同的。
其中把这条路的长度设为1,计算更简便。
如果两辆车一起运,多少次能运完这批货物?
答:如果两辆车一起运,
2次能运完这批货物。
这批货物,只用我的车运,6次才能运完。
只用我的车运,3次就
能运完。
= 2(次)
1÷(+ )
1
6
1
3
= 1÷
1
2
课堂练习
加工180个零件,甲单独做要8天完成,乙单独做要12天完成。
现在甲、乙一起做,6天能完成吗?
= 4.8(天)
1÷(+ )
1
8
1
12
= 1÷
5
24
4.8 < 6
答:甲、乙一起做,6天能完成。
课堂练习
甲、乙两车从两地同时相向开出,甲车行完全程用20小时,乙车行
完全程所用的时间是甲车的 。两车出发多少小时后相遇?
3
2
30 (小时)
20 × =
3
2
= 12(小时)
1÷(+ )
1
20
1
30
= 1÷
1
12
答:两车出发12小时后相遇。
课堂练习
课堂练习
修一条公路,甲队单独修10天完成,乙队单独修15天完成。
两队一起修,多少天能完成全长的 ?
2
3
= 4(天)
2
3
÷(+ )
1
10
1
15
= ÷
1
6
2
3
答:4 天能完成全长的 ?
2
3
将工作总量看作单位“1”,
用单位时间内完成工作总量的几分之一表示工作效率。
基本等量关系式:工作总量÷工作效率之和=工作时间
获
收
我
的
课堂总结
谢谢观看
