华师大版数学八年级下册期末试题【培优】(含答案)
文档属性
| 名称 | 华师大版数学八年级下册期末试题【培优】(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 318.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
华师大版数学八年级下册期末试题【培优】
一、单选题
1.(2023八上·长葛期中)一根细铁丝长,小明想把它折成一个三角形,则他折成的三角形的最长的边有可能是( )
A. B. C. D.
2.(2024八上·白城月考)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.240° B.360° C.540° D.720°
3.(2022八上·东光月考)如图,已知,线段与交于点O,则下面的结论中不正确的是( )
A. B. C. D.
4.(2023八下·紫金月考)如图所示,一副三角板叠放在一起,则图中等于( )
A.105° B.115° C.120° D.135°
5.(2024八上·泸县期中)一木工师傅有两根长分别为的木条,他要找第三根木条,将它们钉成一个三角形框架,以下4根木条,他选择( )根木条合适
A.2cm B.3cm C.10cm D.13cm
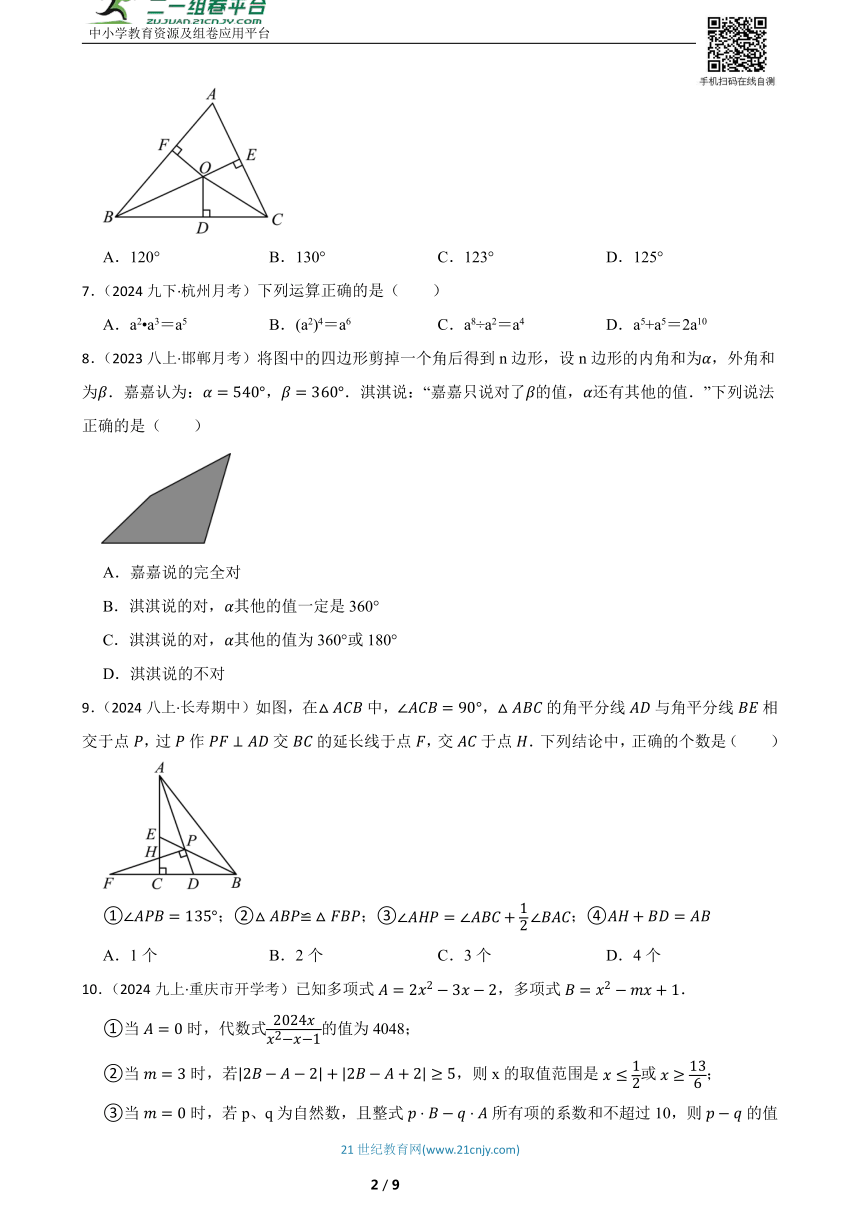
6.(2023八上·路北期末)如图,是内一点,且到三边、、的距离,若,则( )
A.120° B.130° C.123° D.125°
7.(2024九下·杭州月考)下列运算正确的是( )
A.a2 a3=a5 B.(a2)4=a6 C.a8÷a2=a4 D.a5+a5=2a10
8.(2023八上·邯郸月考)将图中的四边形剪掉一个角后得到n边形,设n边形的内角和为,外角和为.嘉嘉认为:,.淇淇说:“嘉嘉只说对了的值,还有其他的值.”下列说法正确的是( )
A.嘉嘉说的完全对
B.淇淇说的对,其他的值一定是360°
C.淇淇说的对,其他的值为360°或180°
D.淇淇说的不对
9.(2024八上·长寿期中)如图,在中,,的角平分线与角平分线相交于点,过作交的延长线于点,交于点.下列结论中,正确的个数是( )
①;②;③;④
A.1个 B.2个 C.3个 D.4个
10.(2024九上·重庆市开学考)已知多项式,多项式.
①当时,代数式的值为4048;
②当时,若,则x的取值范围是或;
③当时,若p、q为自然数,且整式所有项的系数和不超过10,则的值有9种可能.
以上说法正确的个数是( )
A.0 B.1 C.2 D.3
二、填空题
11.(2023八上·莎车期中)点A(3,﹣1)关于y轴对称的点的坐标是 .
12.(2024七下·北京市期中)已知点O为直线上一点,,于点O,平分,则 .
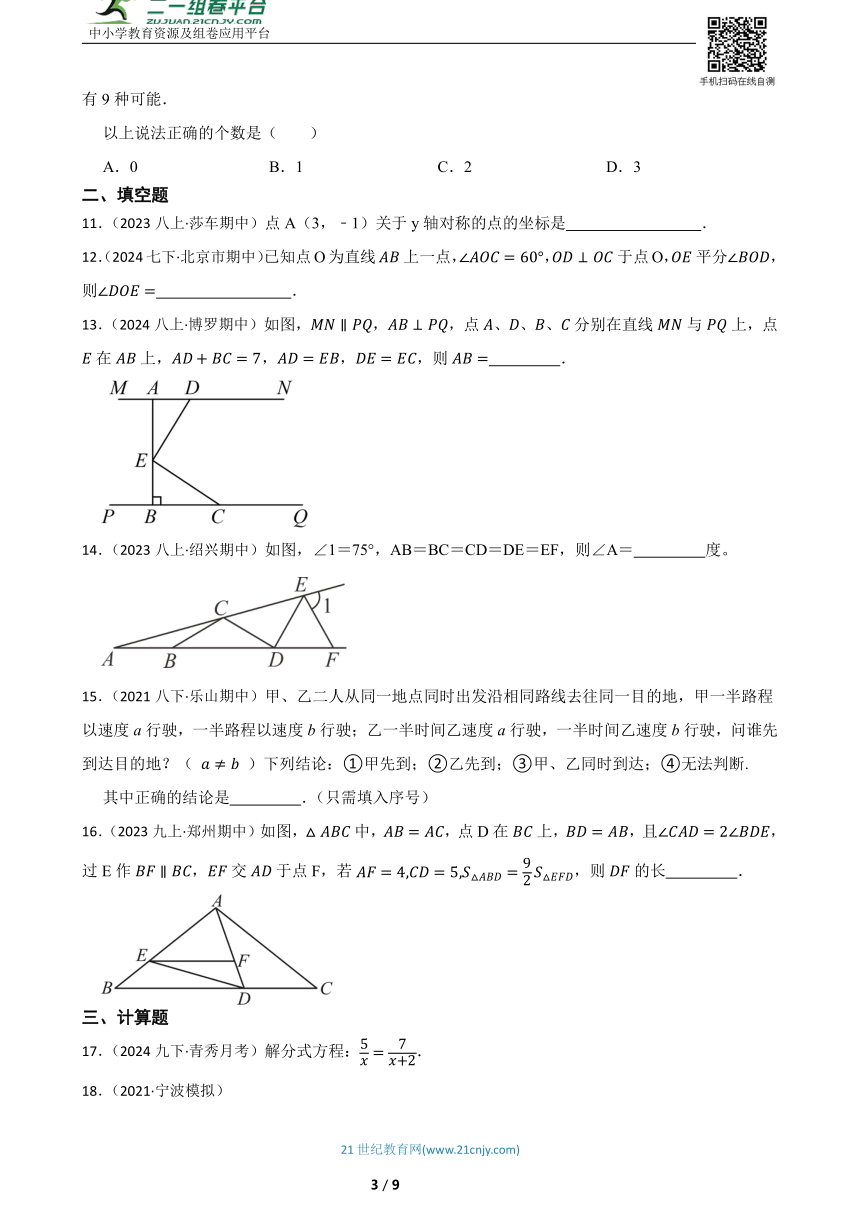
13.(2024八上·博罗期中)如图,,,点、、、分别在直线与上,点在上,,,,则 .
14.(2023八上·绍兴期中)如图,∠1=75°,AB=BC=CD=DE=EF,则∠A= 度。
15.(2021八下·乐山期中)甲、乙二人从同一地点同时出发沿相同路线去往同一目的地,甲一半路程以速度a行驶,一半路程以速度b行驶;乙一半时间乙速度a行驶,一半时间乙速度b行驶,问谁先到达目的地?( )下列结论:①甲先到;②乙先到;③甲、乙同时到达;④无法判断.
其中正确的结论是 .(只需填入序号)
16.(2023九上·郑州期中)如图,中,,点D在上,,且,过E作,交于点F,若,则的长 .
三、计算题
17.(2024九下·青秀月考)解分式方程:.
18.(2021·宁波模拟)
(1)化简: ;
(2)解不等式: .
19.(2017·盐城)先化简,再求值: ÷(x+2﹣ ),其中x=3+ .
四、解答题
20.(2024八上·富顺月考)如图,在中,为的平分线,于E,于F,面积是,,,求的长.
21.(2022八上·大兴期中)用一条长的细绳围成一个等腰三角形,若一腰长是底边长的倍,求各边的长.
22.(2020八上·和平期末)如图所示,在平面直角坐标系中△ABC的三个顶点坐标分别为A(﹣2,4),B(-4,2),C(﹣3,1).
(1)作出△ABC关于x轴对称的△A1B1C1,并直接写出A1点的坐标
(2)作出△ABC关于y轴对称的△A2B2C2,并直接写出B2点的坐标
(3)在(1)(2)的条件下,若点P在x轴上,当A1P+B2P的值最小时,直接写出A1P+B2P的最小值
23.已知 abc=1,则 求 的值.
24.(2024八上·双辽期末)某商场用元购进一批滑板车,很受儿童喜爱,滑板车很快售完,接着又用元购进第二批这种滑板车,所购数量是第一批数量的倍,但每台进价多了元.
(1)求第一批滑板车每台的进价是多少元;
(2)如果这两批滑板车每台售价都是元,那么全部售出后,该商店可获得的利润是多少元?
25.如图, 将一个边长为 的正方形图形分割成四部分(两个正方形和两个长方形), 请认真观察图形, 解答下列问题:
(1)请用两种方法表示该图形阴影部分的面积(用含 的代数式表示):
方法一: ; 方法二: .
(2) 若图中 满足 , 求阴影部分正方形的边长;
(3) 若 , 求 的值.
答案解析部分
1.【答案】A
【知识点】一元一次不等式的应用;三角形三边关系
2.【答案】B
【知识点】三角形的外角性质;多边形内角与外角
3.【答案】C
【知识点】三角形全等及其性质
4.【答案】A
【知识点】角的运算;三角形的外角性质
5.【答案】C
【知识点】三角形三边关系
6.【答案】C
【知识点】三角形内角和定理;角平分线的性质
7.【答案】A
【知识点】同底数幂的乘法;同底数幂的除法;合并同类项法则及应用;幂的乘方运算
8.【答案】C
【知识点】多边形内角与外角
9.【答案】D
【知识点】三角形内角和定理;三角形的外角性质;三角形全等及其性质
10.【答案】C
【知识点】整式的加减运算;分式的值;一元一次不等式的特殊解
11.【答案】(-3,-1)
【知识点】坐标与图形变化﹣对称
12.【答案】或
【知识点】角平分线的性质;邻补角
13.【答案】7
【知识点】平行线的性质;直角三角形全等的判定-HL
14.【答案】15
【知识点】三角形的外角性质;等腰三角形的性质
15.【答案】②
【知识点】分式方程的实际应用
16.【答案】2
【知识点】解分式方程;三角形全等及其性质;等腰三角形的判定与性质
17.【答案】
【知识点】解分式方程
18.【答案】(1)解:原式
.
(2)解:去分母得: ,
去括号得: ,
移项,合并同类项得: ,
系数化为1得: .
【知识点】整式的混合运算;解一元一次不等式
19.【答案】解:原式= ÷( ﹣ )
= ÷
=
= ,
当x=3+ 时,原式= = =
【知识点】分式的化简求值
20.【答案】
【知识点】角平分线的性质
21.【答案】解:设底长为 ,则腰边长为 ,
根据题意得 ,
解得 ,
当 时, ,
所以三角形的腰长为 、 ,底边长为 ,符合题意;
【知识点】等腰三角形的性质
22.【答案】解:(1)分别找出点A、B、C关于x轴的对称点A1、B1、C1,然后顺次连接,如图所示,△A1B1C1即为所求, (-2,-4);
(2)分别找出点A、B、C关于y轴的对称点A2、B2、C2,然后顺次连接,如图所示,△A2B2C2即为所求,
(4,2);
(3)连接A1 B2,交x轴于点P,根据两点之间线段最短可得,A1B2即为A1P+B2P的最小值 .
【知识点】作图﹣轴对称;轴对称的应用-最短距离问题
23.【答案】解:∵abc=1,
∴原式
=1.
【知识点】分式的化简求值-整体代入
24.【答案】(1)解:设第一批滑板车每台的进价是元,则第二批为元,
依题意得:
,
解得,
经检验是原方程的解,
答:第一批滑板车每台的进价是元.
(2)解:由(1)可知第一批购进:(台),
第二批购进(台),
,
答:商店可获得的利润8000元.
【知识点】分式方程的实际应用
25.【答案】(1);
(2)解:∵a2+b2=31,ab=3,
∴结合(1)的结论可得:(a-b)2=a2-2ab+b2
=31-2×3=31-6=25,
∵阴影部分是正方形,
∴阴影部分正方形的边长为:=5.
答:阴影部分正方形的边长是5.
(3)解:设2021-y=m,2023-y=n,
∴mn=1010,m-n=-2,
∴m2+n2=(m-n)2+2mn=(-2)2+2×1010=2024;
即(2021-y)2+(2023-y)2=2024.
答: 的值为 2024
【知识点】多项式乘多项式;完全平方公式的几何背景
21世纪教育网(www.21cnjy.com)
2 / 9
华师大版数学八年级下册期末试题【培优】
一、单选题
1.(2023八上·长葛期中)一根细铁丝长,小明想把它折成一个三角形,则他折成的三角形的最长的边有可能是( )
A. B. C. D.
2.(2024八上·白城月考)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
A.240° B.360° C.540° D.720°
3.(2022八上·东光月考)如图,已知,线段与交于点O,则下面的结论中不正确的是( )
A. B. C. D.
4.(2023八下·紫金月考)如图所示,一副三角板叠放在一起,则图中等于( )
A.105° B.115° C.120° D.135°
5.(2024八上·泸县期中)一木工师傅有两根长分别为的木条,他要找第三根木条,将它们钉成一个三角形框架,以下4根木条,他选择( )根木条合适
A.2cm B.3cm C.10cm D.13cm
6.(2023八上·路北期末)如图,是内一点,且到三边、、的距离,若,则( )
A.120° B.130° C.123° D.125°
7.(2024九下·杭州月考)下列运算正确的是( )
A.a2 a3=a5 B.(a2)4=a6 C.a8÷a2=a4 D.a5+a5=2a10
8.(2023八上·邯郸月考)将图中的四边形剪掉一个角后得到n边形,设n边形的内角和为,外角和为.嘉嘉认为:,.淇淇说:“嘉嘉只说对了的值,还有其他的值.”下列说法正确的是( )
A.嘉嘉说的完全对
B.淇淇说的对,其他的值一定是360°
C.淇淇说的对,其他的值为360°或180°
D.淇淇说的不对
9.(2024八上·长寿期中)如图,在中,,的角平分线与角平分线相交于点,过作交的延长线于点,交于点.下列结论中,正确的个数是( )
①;②;③;④
A.1个 B.2个 C.3个 D.4个
10.(2024九上·重庆市开学考)已知多项式,多项式.
①当时,代数式的值为4048;
②当时,若,则x的取值范围是或;
③当时,若p、q为自然数,且整式所有项的系数和不超过10,则的值有9种可能.
以上说法正确的个数是( )
A.0 B.1 C.2 D.3
二、填空题
11.(2023八上·莎车期中)点A(3,﹣1)关于y轴对称的点的坐标是 .
12.(2024七下·北京市期中)已知点O为直线上一点,,于点O,平分,则 .
13.(2024八上·博罗期中)如图,,,点、、、分别在直线与上,点在上,,,,则 .
14.(2023八上·绍兴期中)如图,∠1=75°,AB=BC=CD=DE=EF,则∠A= 度。
15.(2021八下·乐山期中)甲、乙二人从同一地点同时出发沿相同路线去往同一目的地,甲一半路程以速度a行驶,一半路程以速度b行驶;乙一半时间乙速度a行驶,一半时间乙速度b行驶,问谁先到达目的地?( )下列结论:①甲先到;②乙先到;③甲、乙同时到达;④无法判断.
其中正确的结论是 .(只需填入序号)
16.(2023九上·郑州期中)如图,中,,点D在上,,且,过E作,交于点F,若,则的长 .
三、计算题
17.(2024九下·青秀月考)解分式方程:.
18.(2021·宁波模拟)
(1)化简: ;
(2)解不等式: .
19.(2017·盐城)先化简,再求值: ÷(x+2﹣ ),其中x=3+ .
四、解答题
20.(2024八上·富顺月考)如图,在中,为的平分线,于E,于F,面积是,,,求的长.
21.(2022八上·大兴期中)用一条长的细绳围成一个等腰三角形,若一腰长是底边长的倍,求各边的长.
22.(2020八上·和平期末)如图所示,在平面直角坐标系中△ABC的三个顶点坐标分别为A(﹣2,4),B(-4,2),C(﹣3,1).
(1)作出△ABC关于x轴对称的△A1B1C1,并直接写出A1点的坐标
(2)作出△ABC关于y轴对称的△A2B2C2,并直接写出B2点的坐标
(3)在(1)(2)的条件下,若点P在x轴上,当A1P+B2P的值最小时,直接写出A1P+B2P的最小值
23.已知 abc=1,则 求 的值.
24.(2024八上·双辽期末)某商场用元购进一批滑板车,很受儿童喜爱,滑板车很快售完,接着又用元购进第二批这种滑板车,所购数量是第一批数量的倍,但每台进价多了元.
(1)求第一批滑板车每台的进价是多少元;
(2)如果这两批滑板车每台售价都是元,那么全部售出后,该商店可获得的利润是多少元?
25.如图, 将一个边长为 的正方形图形分割成四部分(两个正方形和两个长方形), 请认真观察图形, 解答下列问题:
(1)请用两种方法表示该图形阴影部分的面积(用含 的代数式表示):
方法一: ; 方法二: .
(2) 若图中 满足 , 求阴影部分正方形的边长;
(3) 若 , 求 的值.
答案解析部分
1.【答案】A
【知识点】一元一次不等式的应用;三角形三边关系
2.【答案】B
【知识点】三角形的外角性质;多边形内角与外角
3.【答案】C
【知识点】三角形全等及其性质
4.【答案】A
【知识点】角的运算;三角形的外角性质
5.【答案】C
【知识点】三角形三边关系
6.【答案】C
【知识点】三角形内角和定理;角平分线的性质
7.【答案】A
【知识点】同底数幂的乘法;同底数幂的除法;合并同类项法则及应用;幂的乘方运算
8.【答案】C
【知识点】多边形内角与外角
9.【答案】D
【知识点】三角形内角和定理;三角形的外角性质;三角形全等及其性质
10.【答案】C
【知识点】整式的加减运算;分式的值;一元一次不等式的特殊解
11.【答案】(-3,-1)
【知识点】坐标与图形变化﹣对称
12.【答案】或
【知识点】角平分线的性质;邻补角
13.【答案】7
【知识点】平行线的性质;直角三角形全等的判定-HL
14.【答案】15
【知识点】三角形的外角性质;等腰三角形的性质
15.【答案】②
【知识点】分式方程的实际应用
16.【答案】2
【知识点】解分式方程;三角形全等及其性质;等腰三角形的判定与性质
17.【答案】
【知识点】解分式方程
18.【答案】(1)解:原式
.
(2)解:去分母得: ,
去括号得: ,
移项,合并同类项得: ,
系数化为1得: .
【知识点】整式的混合运算;解一元一次不等式
19.【答案】解:原式= ÷( ﹣ )
= ÷
=
= ,
当x=3+ 时,原式= = =
【知识点】分式的化简求值
20.【答案】
【知识点】角平分线的性质
21.【答案】解:设底长为 ,则腰边长为 ,
根据题意得 ,
解得 ,
当 时, ,
所以三角形的腰长为 、 ,底边长为 ,符合题意;
【知识点】等腰三角形的性质
22.【答案】解:(1)分别找出点A、B、C关于x轴的对称点A1、B1、C1,然后顺次连接,如图所示,△A1B1C1即为所求, (-2,-4);
(2)分别找出点A、B、C关于y轴的对称点A2、B2、C2,然后顺次连接,如图所示,△A2B2C2即为所求,
(4,2);
(3)连接A1 B2,交x轴于点P,根据两点之间线段最短可得,A1B2即为A1P+B2P的最小值 .
【知识点】作图﹣轴对称;轴对称的应用-最短距离问题
23.【答案】解:∵abc=1,
∴原式
=1.
【知识点】分式的化简求值-整体代入
24.【答案】(1)解:设第一批滑板车每台的进价是元,则第二批为元,
依题意得:
,
解得,
经检验是原方程的解,
答:第一批滑板车每台的进价是元.
(2)解:由(1)可知第一批购进:(台),
第二批购进(台),
,
答:商店可获得的利润8000元.
【知识点】分式方程的实际应用
25.【答案】(1);
(2)解:∵a2+b2=31,ab=3,
∴结合(1)的结论可得:(a-b)2=a2-2ab+b2
=31-2×3=31-6=25,
∵阴影部分是正方形,
∴阴影部分正方形的边长为:=5.
答:阴影部分正方形的边长是5.
(3)解:设2021-y=m,2023-y=n,
∴mn=1010,m-n=-2,
∴m2+n2=(m-n)2+2mn=(-2)2+2×1010=2024;
即(2021-y)2+(2023-y)2=2024.
答: 的值为 2024
【知识点】多项式乘多项式;完全平方公式的几何背景
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
