第八章 认识概率 章末练习【培优】(含答案)
文档属性
| 名称 | 第八章 认识概率 章末练习【培优】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 804.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 04:30:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章 认识概率【培优】
一、单选题
1.(2024九上·东阳期末)下列诗句所描述的事件中,属于不可能事件的是( )
A.守株待兔 B.瓮中捉鳖 C.水中捞月 D.百步穿杨
2.(2024九上·西湖月考)下列四个图形中,从中任取一个是中心对称图形的概率是( )
A. B. C. D.1
3.(2024九下·高坪模拟)下列说法正确的是( )
A.要了解七年级(一)班学生的视力情况,适合采用抽样调查
B.李老师想了解小菲同学4次数学模拟考试成绩的变化情况应选用折线统计图
C.事件“乘坐公共汽车恰好有空座”是必然事件
D.掷一枚质地均匀的硬币两次,一定有一次正面朝上
4.(2024九下·岳阳模拟)某同学现有一装有若干个黄球的袋子.为了估计袋子中黄球的数量,该同学向这袋黄球中放入了30个绿球(所有球除颜色外其余均相同),摇匀后随机抓取60个,其中绿球共计10个,则袋子中黄球的数量约为( )
A.200个 B.180个 C.240个 D.150个
5.(2024九上·越城期末)在一个不透明的口袋中有除颜色外完全相同的5个白球、7个红球,则任意摸出一个球是红球的概率是( )
A. B. C. D.1
6.(2024九上·鹿城期中)小明在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制统计图如图所示,则符合这一结果的实验可能是( )
A.掷一枚正六面体的骰子,出现4点的概率
B.抛一枚硬币,出现反面的概率
C.任意写一个正整数,它能被3整除的概率
D.从一副扑克牌中任抽一张牌,取到“大王”的概率
7.(2024九上·东阳期中)一个袋子里有7个红球、4个黄球和1个绿球。从中任意摸出1个球,摸出的球( )。
A.一定是绿球 B.一定是黄球
C.一定是红球 D.红球的可能性大
8.(2024九上·清远期末)林业局为考察一种树苗移植的成活率,展开了大量调查,并将调查数据绘制成如图所示的统计图,则可估计这种树苗移植成活的概率为( )
A. B. C. D.
9.(2024九上·英德期中)某区为了解初中生体质健康水平,在全区进行初中生体质健康的随机抽测,结果如下表,根据抽测结果,下列对该区初中生体质健康合格的概率的估计,最合理的是( )
累计抽测的学生数n 100 200 300 400 500 600 700 800 900 1000
体质健康合格的学生数与n的比值 0.85 0.9 0.93 0.9 0.89 0.9 0.91 0.91 0.92 0.92
A.0.92 B.0.91 C.0.903 D.0.9
10.(2024七上·成都开学考)投掷3次硬币,有2次正面朝上,1次反面朝上,那么第4次投掷硬币正面朝上的可能性是( )
A. B. C. D.
二、填空题
11.(2024九下·嘉善模拟)一个不透明的袋子里装有6个红球和4个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为 .
12.(2024九下·福田模拟)老师将6种生活现象制成如图所示看上去无差别的卡片,从中随机抽取一张卡,抽中生活现象是物理变化的概率是 .
13.(2024九下·湖南会考)一个不透明的袋子中装有四个小球,它们除了分别标有的数字1,2,3,4不同外,其它完全相同,任意从袋子中摸出一球后不放回,再任意摸出一球,则两次摸出的球所标数字之和为5的概率是 .
14.(2024九上·绍兴月考)一个不透明的盒子中装有若干个红球和个黑球,这些球除颜色外均相同.经多次摸球试验后发现,摸到黑球的频率稳定在左右,则盒子中红球的个数约为 .
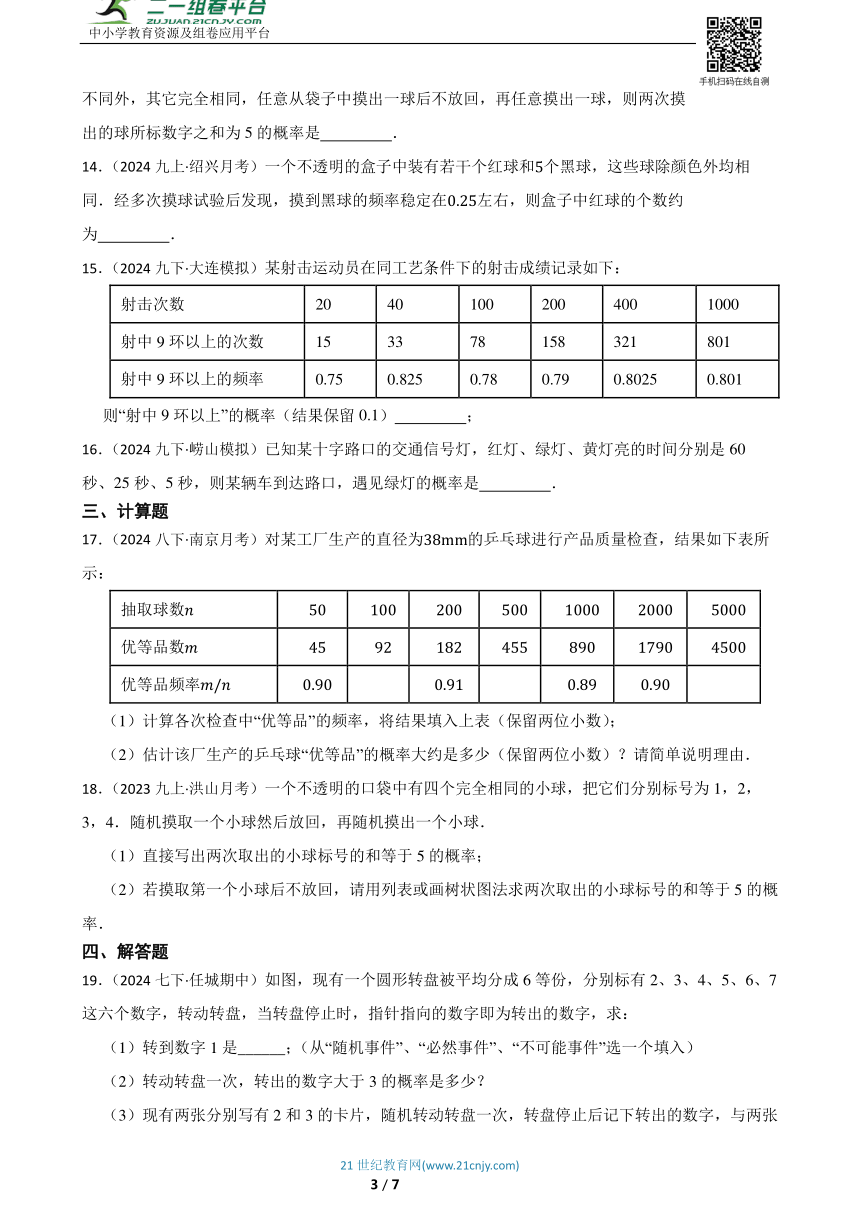
15.(2024九下·大连模拟)某射击运动员在同工艺条件下的射击成绩记录如下:
射击次数 20 40 100 200 400 1000
射中9环以上的次数 15 33 78 158 321 801
射中9环以上的频率 0.75 0.825 0.78 0.79 0.8025 0.801
则“射中9环以上”的概率(结果保留0.1) ;
16.(2024九下·崂山模拟)已知某十字路口的交通信号灯,红灯、绿灯、黄灯亮的时间分别是60秒、25秒、5秒,则某辆车到达路口,遇见绿灯的概率是 .
三、计算题
17.(2024八下·南京月考)对某工厂生产的直径为的乒乓球进行产品质量检查,结果如下表所示:
抽取球数
优等品数
优等品频率
(1)计算各次检查中“优等品”的频率,将结果填入上表(保留两位小数);
(2)估计该厂生产的乒乓球“优等品”的概率大约是多少(保留两位小数)?请简单说明理由.
18.(2023九上·洪山月考)一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球.
(1)直接写出两次取出的小球标号的和等于5的概率;
(2)若摸取第一个小球后不放回,请用列表或画树状图法求两次取出的小球标号的和等于5的概率.
四、解答题
19.(2024七下·任城期中)如图,现有一个圆形转盘被平均分成6等份,分别标有2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)转到数字1是______;(从“随机事件”、“必然事件”、“不可能事件”选一个填入)
(2)转动转盘一次,转出的数字大于3的概率是多少?
(3)现有两张分别写有2和3的卡片,随机转动转盘一次,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度(长度单位均是厘米).这三条线段能构成三角形的概率是多少?
20.如图所示,下列第一排表示了不同组成情况的十张牌,任意抽一张,请选择第二排的语言来描述抽到红牌的可能性,并用线连起来.
21.(2024八下·吴江月考)在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球试验;每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s 150 300 600 900 1200 1500
摸到白球的频数n 63 a 247 365 484 606
摸到白球的频率 b
(1)按表格数据格式,表中的 .
(2)请估计:当次数 s 很大时,摸到白球的频率将会接近 (精确到);
(3)请推算:摸到红球的概率约是 (精确到);
(4)试估算:这一个不透明的口袋中红球有 只.
22.(2024八上·重庆市开学考)在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球试验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s 150 300 600 900 1200 1500
摸到白球的频数n 63 123 247 365 484 606
摸到白球的频率 0.420 0.410 0.412 0.406 0.403 a
(1)按表格数据格式,表中的a=______;
(2)请估计:当次数s很大时,摸到白球的频率将会接近______(精确到0.1);
(3)试估算:这一个不透明的口袋中红球有______只.
答案解析部分
1.【答案】C
【知识点】事件的分类
2.【答案】B
【知识点】中心对称及中心对称图形;概率公式
3.【答案】B
【知识点】全面调查与抽样调查;统计图的选择;事件的分类
4.【答案】D
【知识点】解分式方程;利用频率估计概率
5.【答案】B
【知识点】概率公式
6.【答案】C
【知识点】利用频率估计概率;概率公式
7.【答案】D
【知识点】可能性的大小;概率的意义;事件发生的可能性
8.【答案】B
【知识点】利用频率估计概率
9.【答案】A
【知识点】利用频率估计概率
10.【答案】A
【知识点】可能性的大小
11.【答案】
【知识点】概率公式
12.【答案】
【知识点】概率公式
13.【答案】
【知识点】用列表法或树状图法求概率;概率公式;等可能事件的概率
14.【答案】15
【知识点】利用频率估计概率;概率公式
15.【答案】
【知识点】利用频率估计概率
16.【答案】
【知识点】概率公式
17.【答案】(1)、、
(2)
【知识点】频数与频率;利用频率估计概率
18.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
19.【答案】(1)不可能事件;(2);(3)
【知识点】三角形三边关系;概率公式
20.【答案】解:如图,
【知识点】可能性的大小;事件发生的可能性
21.【答案】(1)
(2)
(3)
(4)
【知识点】解分式方程;利用频率估计概率;概率公式
22.【答案】(1)0.404
(2)0.4
(3)15
【知识点】频数与频率;利用频率估计概率;简单事件概率的计算
21世纪教育网(www.21cnjy.com)
2 / 7
第八章 认识概率【培优】
一、单选题
1.(2024九上·东阳期末)下列诗句所描述的事件中,属于不可能事件的是( )
A.守株待兔 B.瓮中捉鳖 C.水中捞月 D.百步穿杨
2.(2024九上·西湖月考)下列四个图形中,从中任取一个是中心对称图形的概率是( )
A. B. C. D.1
3.(2024九下·高坪模拟)下列说法正确的是( )
A.要了解七年级(一)班学生的视力情况,适合采用抽样调查
B.李老师想了解小菲同学4次数学模拟考试成绩的变化情况应选用折线统计图
C.事件“乘坐公共汽车恰好有空座”是必然事件
D.掷一枚质地均匀的硬币两次,一定有一次正面朝上
4.(2024九下·岳阳模拟)某同学现有一装有若干个黄球的袋子.为了估计袋子中黄球的数量,该同学向这袋黄球中放入了30个绿球(所有球除颜色外其余均相同),摇匀后随机抓取60个,其中绿球共计10个,则袋子中黄球的数量约为( )
A.200个 B.180个 C.240个 D.150个
5.(2024九上·越城期末)在一个不透明的口袋中有除颜色外完全相同的5个白球、7个红球,则任意摸出一个球是红球的概率是( )
A. B. C. D.1
6.(2024九上·鹿城期中)小明在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制统计图如图所示,则符合这一结果的实验可能是( )
A.掷一枚正六面体的骰子,出现4点的概率
B.抛一枚硬币,出现反面的概率
C.任意写一个正整数,它能被3整除的概率
D.从一副扑克牌中任抽一张牌,取到“大王”的概率
7.(2024九上·东阳期中)一个袋子里有7个红球、4个黄球和1个绿球。从中任意摸出1个球,摸出的球( )。
A.一定是绿球 B.一定是黄球
C.一定是红球 D.红球的可能性大
8.(2024九上·清远期末)林业局为考察一种树苗移植的成活率,展开了大量调查,并将调查数据绘制成如图所示的统计图,则可估计这种树苗移植成活的概率为( )
A. B. C. D.
9.(2024九上·英德期中)某区为了解初中生体质健康水平,在全区进行初中生体质健康的随机抽测,结果如下表,根据抽测结果,下列对该区初中生体质健康合格的概率的估计,最合理的是( )
累计抽测的学生数n 100 200 300 400 500 600 700 800 900 1000
体质健康合格的学生数与n的比值 0.85 0.9 0.93 0.9 0.89 0.9 0.91 0.91 0.92 0.92
A.0.92 B.0.91 C.0.903 D.0.9
10.(2024七上·成都开学考)投掷3次硬币,有2次正面朝上,1次反面朝上,那么第4次投掷硬币正面朝上的可能性是( )
A. B. C. D.
二、填空题
11.(2024九下·嘉善模拟)一个不透明的袋子里装有6个红球和4个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为 .
12.(2024九下·福田模拟)老师将6种生活现象制成如图所示看上去无差别的卡片,从中随机抽取一张卡,抽中生活现象是物理变化的概率是 .
13.(2024九下·湖南会考)一个不透明的袋子中装有四个小球,它们除了分别标有的数字1,2,3,4不同外,其它完全相同,任意从袋子中摸出一球后不放回,再任意摸出一球,则两次摸出的球所标数字之和为5的概率是 .
14.(2024九上·绍兴月考)一个不透明的盒子中装有若干个红球和个黑球,这些球除颜色外均相同.经多次摸球试验后发现,摸到黑球的频率稳定在左右,则盒子中红球的个数约为 .
15.(2024九下·大连模拟)某射击运动员在同工艺条件下的射击成绩记录如下:
射击次数 20 40 100 200 400 1000
射中9环以上的次数 15 33 78 158 321 801
射中9环以上的频率 0.75 0.825 0.78 0.79 0.8025 0.801
则“射中9环以上”的概率(结果保留0.1) ;
16.(2024九下·崂山模拟)已知某十字路口的交通信号灯,红灯、绿灯、黄灯亮的时间分别是60秒、25秒、5秒,则某辆车到达路口,遇见绿灯的概率是 .
三、计算题
17.(2024八下·南京月考)对某工厂生产的直径为的乒乓球进行产品质量检查,结果如下表所示:
抽取球数
优等品数
优等品频率
(1)计算各次检查中“优等品”的频率,将结果填入上表(保留两位小数);
(2)估计该厂生产的乒乓球“优等品”的概率大约是多少(保留两位小数)?请简单说明理由.
18.(2023九上·洪山月考)一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球.
(1)直接写出两次取出的小球标号的和等于5的概率;
(2)若摸取第一个小球后不放回,请用列表或画树状图法求两次取出的小球标号的和等于5的概率.
四、解答题
19.(2024七下·任城期中)如图,现有一个圆形转盘被平均分成6等份,分别标有2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)转到数字1是______;(从“随机事件”、“必然事件”、“不可能事件”选一个填入)
(2)转动转盘一次,转出的数字大于3的概率是多少?
(3)现有两张分别写有2和3的卡片,随机转动转盘一次,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度(长度单位均是厘米).这三条线段能构成三角形的概率是多少?
20.如图所示,下列第一排表示了不同组成情况的十张牌,任意抽一张,请选择第二排的语言来描述抽到红牌的可能性,并用线连起来.
21.(2024八下·吴江月考)在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球试验;每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s 150 300 600 900 1200 1500
摸到白球的频数n 63 a 247 365 484 606
摸到白球的频率 b
(1)按表格数据格式,表中的 .
(2)请估计:当次数 s 很大时,摸到白球的频率将会接近 (精确到);
(3)请推算:摸到红球的概率约是 (精确到);
(4)试估算:这一个不透明的口袋中红球有 只.
22.(2024八上·重庆市开学考)在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球试验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s 150 300 600 900 1200 1500
摸到白球的频数n 63 123 247 365 484 606
摸到白球的频率 0.420 0.410 0.412 0.406 0.403 a
(1)按表格数据格式,表中的a=______;
(2)请估计:当次数s很大时,摸到白球的频率将会接近______(精确到0.1);
(3)试估算:这一个不透明的口袋中红球有______只.
答案解析部分
1.【答案】C
【知识点】事件的分类
2.【答案】B
【知识点】中心对称及中心对称图形;概率公式
3.【答案】B
【知识点】全面调查与抽样调查;统计图的选择;事件的分类
4.【答案】D
【知识点】解分式方程;利用频率估计概率
5.【答案】B
【知识点】概率公式
6.【答案】C
【知识点】利用频率估计概率;概率公式
7.【答案】D
【知识点】可能性的大小;概率的意义;事件发生的可能性
8.【答案】B
【知识点】利用频率估计概率
9.【答案】A
【知识点】利用频率估计概率
10.【答案】A
【知识点】可能性的大小
11.【答案】
【知识点】概率公式
12.【答案】
【知识点】概率公式
13.【答案】
【知识点】用列表法或树状图法求概率;概率公式;等可能事件的概率
14.【答案】15
【知识点】利用频率估计概率;概率公式
15.【答案】
【知识点】利用频率估计概率
16.【答案】
【知识点】概率公式
17.【答案】(1)、、
(2)
【知识点】频数与频率;利用频率估计概率
18.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
19.【答案】(1)不可能事件;(2);(3)
【知识点】三角形三边关系;概率公式
20.【答案】解:如图,
【知识点】可能性的大小;事件发生的可能性
21.【答案】(1)
(2)
(3)
(4)
【知识点】解分式方程;利用频率估计概率;概率公式
22.【答案】(1)0.404
(2)0.4
(3)15
【知识点】频数与频率;利用频率估计概率;简单事件概率的计算
21世纪教育网(www.21cnjy.com)
2 / 7
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
