9.3平行四边形 同步练习(含答案)
文档属性
| 名称 | 9.3平行四边形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 183.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 04:33:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
9.3平行四边形
一、单选题
1.如图,在中,若,则的度数是( )
A. B. C. D.
2.下列命题的逆命题是真命题的是( )
A.对顶角相等
B.如果两个实数相等,那么它们的绝对值相等
C.等边三角形的三个内角都等于60°
D.平行四边形的一组对边相等
3.如图,在中,平分,交边于,,,则的长为( )
A. B. C. D.
4.如图,在中,AC,BD相交于点O,若,则线段AO的长为( )
A.3 B.4 C.5 D.16
5.如图,在中,,的角平分线交于点E,连接,若恰好垂直于,则的值为( )
A.64 B.36 C.20 D.16
二、填空题
6.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成了一个四边形ABCD,当线段AD=13时,线段BC的长为 .
7.如图,在中,,,,则 .
8.如图,在中,,,的平分线交,则 .
9. ABCD一内角的平分线与边相交并把这条边分成5cm,7cm的两条线段,则 ABCD的周长是 cm.
10.四边形中,,当 时,这个四边形是平行四边形.
11.如图,在平行四边形中,对角线相交于点O.已知两条对角线长的和为,长为.则的周长为 .
三、计算题
12.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
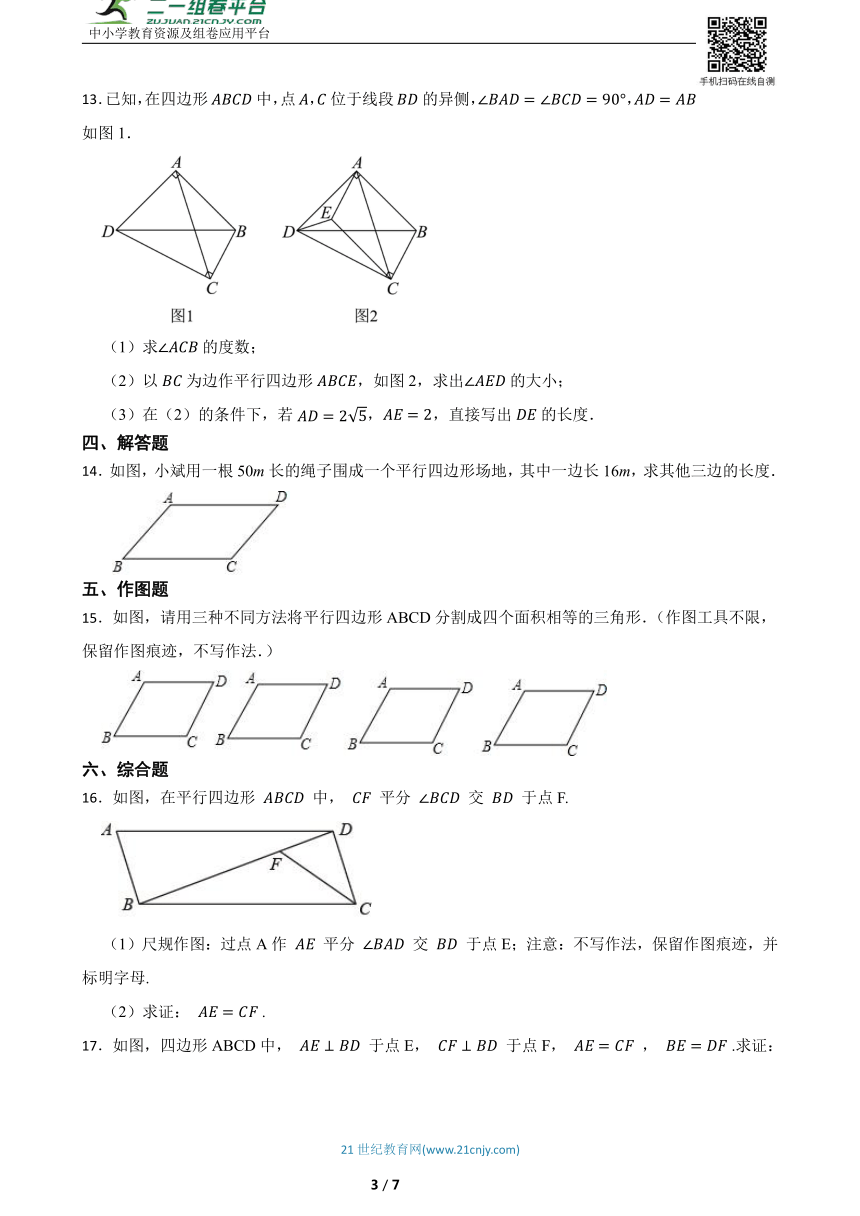
13.已知,在四边形中,点,位于线段的异侧,,,如图1.
(1)求的度数;
(2)以为边作平行四边形,如图2,求出的大小;
(3)在(2)的条件下,若,,直接写出的长度.
四、解答题
14.如图,小斌用一根50m长的绳子围成一个平行四边形场地,其中一边长16m,求其他三边的长度.
五、作图题
15.如图,请用三种不同方法将平行四边形ABCD分割成四个面积相等的三角形.(作图工具不限,保留作图痕迹,不写作法.)
六、综合题
16.如图,在平行四边形 中, 平分 交 于点F.
(1)尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.
(2)求证: .
17.如图,四边形ABCD中, 于点E, 于点F, , .求证:
(1) ;
(2)四边形ABCD是平行四边形.
18.如图,在方格网中已知格点△ABC和点O.
(1)画△A′B′C′和△ABC关于点O成中心对称;
(2)请在方格网中标出所有使以点A、O、C′、D为顶点的四边形是平行四边形的D点.
答案解析部分
1.【答案】C
【知识点】平行四边形的性质
2.【答案】C
【知识点】平行四边形的判定;真命题与假命题;逆命题;绝对值的概念与意义
3.【答案】C
【知识点】等腰三角形的判定与性质;平行四边形的性质
4.【答案】B
【知识点】平行四边形的性质
5.【答案】A
【知识点】等腰三角形的判定与性质;勾股定理;平行四边形的性质
6.【答案】13
【知识点】平行四边形的判定与性质
7.【答案】10
【知识点】勾股定理;平行四边形的性质
8.【答案】4
【知识点】角平分线的性质;等腰三角形的判定与性质;平行四边形的性质
9.【答案】34或38
【知识点】平行四边形的性质
10.【答案】3
【知识点】平行四边形的判定
11.【答案】
【知识点】平行四边形的性质
12.【答案】解:∵在平行四边形ABCD中,AB∥CD且AB=CD
又∵AE=CF
∴AB-AE=CD-CF
∴BE=DF
∴四边形EBFD是平行四边形
∴DE=BF.
【知识点】平行四边形的判定与性质
13.【答案】(1)
(2)
(3)
【知识点】等腰三角形的判定与性质;勾股定理;平行四边形的性质;三角形全等的判定-SAS
14.【答案】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵周长为50,
∴2(AB+BC)=50,
∴AB+BC=25,
∵一边长为16m,
∴另一边长为9m,
∴其他三边的长为9m,16m,9m.
【知识点】平行四边形的性质
15.【答案】解:如图所示:
【知识点】三角形的面积;平行四边形的性质
16.【答案】(1)解:如图,AE为所作;
(2)证明:∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE BAD,∠DCF ∠BCD,
∵四边形ABCD为平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵AB∥CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AE=CF.
【知识点】平行四边形的性质;三角形全等的判定-ASA;角平分线的概念;尺规作图-作角的平分线
17.【答案】(1)解:∵ ,
∴∠AEB=∠CFD=90°
又∵ ,
∴ (SAS)
(2)解:∵
∴∠ABE=∠CDF,AB=CD,
∴AB∥CD
∴四边形ABCD是平行四边形
【知识点】平行四边形的判定;三角形全等的判定-SAS
18.【答案】(1)解:画△A′B′C′和△ABC关于点O成中心对称的图形如下:
(2)解:根据题意画图如下:
【知识点】平行四边形的判定;作图﹣旋转
21世纪教育网(www.21cnjy.com)
1 / 7
9.3平行四边形
一、单选题
1.如图,在中,若,则的度数是( )
A. B. C. D.
2.下列命题的逆命题是真命题的是( )
A.对顶角相等
B.如果两个实数相等,那么它们的绝对值相等
C.等边三角形的三个内角都等于60°
D.平行四边形的一组对边相等
3.如图,在中,平分,交边于,,,则的长为( )
A. B. C. D.
4.如图,在中,AC,BD相交于点O,若,则线段AO的长为( )
A.3 B.4 C.5 D.16
5.如图,在中,,的角平分线交于点E,连接,若恰好垂直于,则的值为( )
A.64 B.36 C.20 D.16
二、填空题
6.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成了一个四边形ABCD,当线段AD=13时,线段BC的长为 .
7.如图,在中,,,,则 .
8.如图,在中,,,的平分线交,则 .
9. ABCD一内角的平分线与边相交并把这条边分成5cm,7cm的两条线段,则 ABCD的周长是 cm.
10.四边形中,,当 时,这个四边形是平行四边形.
11.如图,在平行四边形中,对角线相交于点O.已知两条对角线长的和为,长为.则的周长为 .
三、计算题
12.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
13.已知,在四边形中,点,位于线段的异侧,,,如图1.
(1)求的度数;
(2)以为边作平行四边形,如图2,求出的大小;
(3)在(2)的条件下,若,,直接写出的长度.
四、解答题
14.如图,小斌用一根50m长的绳子围成一个平行四边形场地,其中一边长16m,求其他三边的长度.
五、作图题
15.如图,请用三种不同方法将平行四边形ABCD分割成四个面积相等的三角形.(作图工具不限,保留作图痕迹,不写作法.)
六、综合题
16.如图,在平行四边形 中, 平分 交 于点F.
(1)尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.
(2)求证: .
17.如图,四边形ABCD中, 于点E, 于点F, , .求证:
(1) ;
(2)四边形ABCD是平行四边形.
18.如图,在方格网中已知格点△ABC和点O.
(1)画△A′B′C′和△ABC关于点O成中心对称;
(2)请在方格网中标出所有使以点A、O、C′、D为顶点的四边形是平行四边形的D点.
答案解析部分
1.【答案】C
【知识点】平行四边形的性质
2.【答案】C
【知识点】平行四边形的判定;真命题与假命题;逆命题;绝对值的概念与意义
3.【答案】C
【知识点】等腰三角形的判定与性质;平行四边形的性质
4.【答案】B
【知识点】平行四边形的性质
5.【答案】A
【知识点】等腰三角形的判定与性质;勾股定理;平行四边形的性质
6.【答案】13
【知识点】平行四边形的判定与性质
7.【答案】10
【知识点】勾股定理;平行四边形的性质
8.【答案】4
【知识点】角平分线的性质;等腰三角形的判定与性质;平行四边形的性质
9.【答案】34或38
【知识点】平行四边形的性质
10.【答案】3
【知识点】平行四边形的判定
11.【答案】
【知识点】平行四边形的性质
12.【答案】解:∵在平行四边形ABCD中,AB∥CD且AB=CD
又∵AE=CF
∴AB-AE=CD-CF
∴BE=DF
∴四边形EBFD是平行四边形
∴DE=BF.
【知识点】平行四边形的判定与性质
13.【答案】(1)
(2)
(3)
【知识点】等腰三角形的判定与性质;勾股定理;平行四边形的性质;三角形全等的判定-SAS
14.【答案】解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵周长为50,
∴2(AB+BC)=50,
∴AB+BC=25,
∵一边长为16m,
∴另一边长为9m,
∴其他三边的长为9m,16m,9m.
【知识点】平行四边形的性质
15.【答案】解:如图所示:
【知识点】三角形的面积;平行四边形的性质
16.【答案】(1)解:如图,AE为所作;
(2)证明:∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE BAD,∠DCF ∠BCD,
∵四边形ABCD为平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵AB∥CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AE=CF.
【知识点】平行四边形的性质;三角形全等的判定-ASA;角平分线的概念;尺规作图-作角的平分线
17.【答案】(1)解:∵ ,
∴∠AEB=∠CFD=90°
又∵ ,
∴ (SAS)
(2)解:∵
∴∠ABE=∠CDF,AB=CD,
∴AB∥CD
∴四边形ABCD是平行四边形
【知识点】平行四边形的判定;三角形全等的判定-SAS
18.【答案】(1)解:画△A′B′C′和△ABC关于点O成中心对称的图形如下:
(2)解:根据题意画图如下:
【知识点】平行四边形的判定;作图﹣旋转
21世纪教育网(www.21cnjy.com)
1 / 7
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
