9.4矩形 ,菱形,正方形 同步练习(含答案)
文档属性
| 名称 | 9.4矩形 ,菱形,正方形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 645.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 04:33:44 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
9.4矩形 ,菱形,正方形
一、单选题
1.将矩形纸片放置在如图所示的平面直角坐标系中,P为边上一动点(不与点B,C重合),连接,将折叠,得到.经过点P再次折叠纸片,使点B的对应点落在直线上,折痕交于点E.已知点,当四边形是正方形时,点E的坐标为( )
A. B. C. D.
2.下列是关于某个四边形的三个结论:①它是一个菱形;②它的对角线互相垂直;③它是一个正方形.下列推理过程正确的是( )
A.由①推出②,由②推出③ B.由②推出③,由③推出①
C.由③推出①,由①推出③ D.由③推出①,由①推出②
3.下列命题中是真命题的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线互相垂直且平分的四边形是菱形
C.有一个角是直角且对角线相等的四边形是矩形
D.一个角为且一组邻边相等的四边形是正方形
4.若菱形的两条对角线的长分别为6和10,则菱形的面积为( )
A.60 B.30 C.24 D.15
5.如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为(
A.8 B.9 C.10 D.11
二、填空题
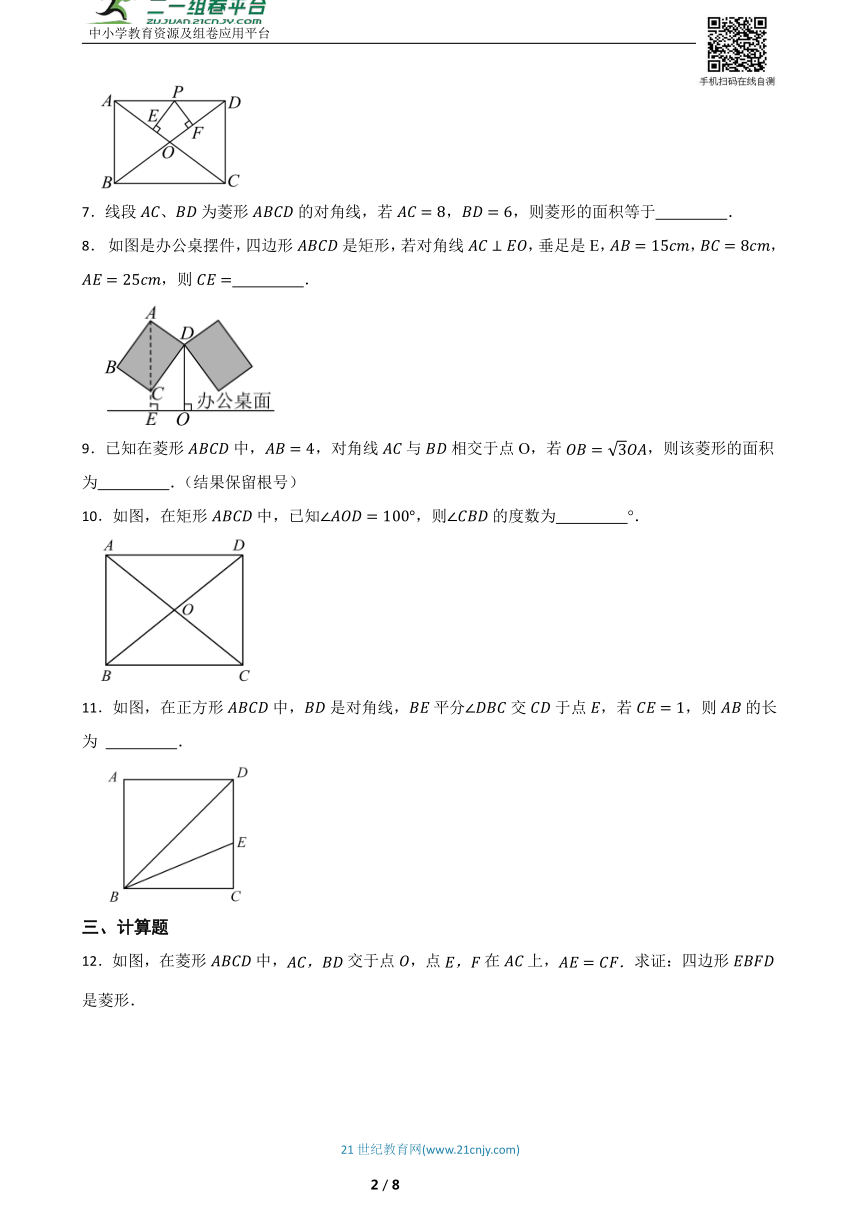
6.如图,矩形中,,,是上的一个动点,于,于,则的值为 .
7.线段、为菱形的对角线,若,,则菱形的面积等于 .
8. 如图是办公桌摆件,四边形是矩形,若对角线,垂足是E,,,,则 .
9.已知在菱形中,,对角线与相交于点O,若,则该菱形的面积为 .(结果保留根号)
10.如图,在矩形中,已知,则的度数为 °.
11.如图,在正方形中,是对角线,平分交于点,若,则的长为 .
三、计算题
12.如图,在菱形中,交于点,点在上,求证:四边形是菱形.
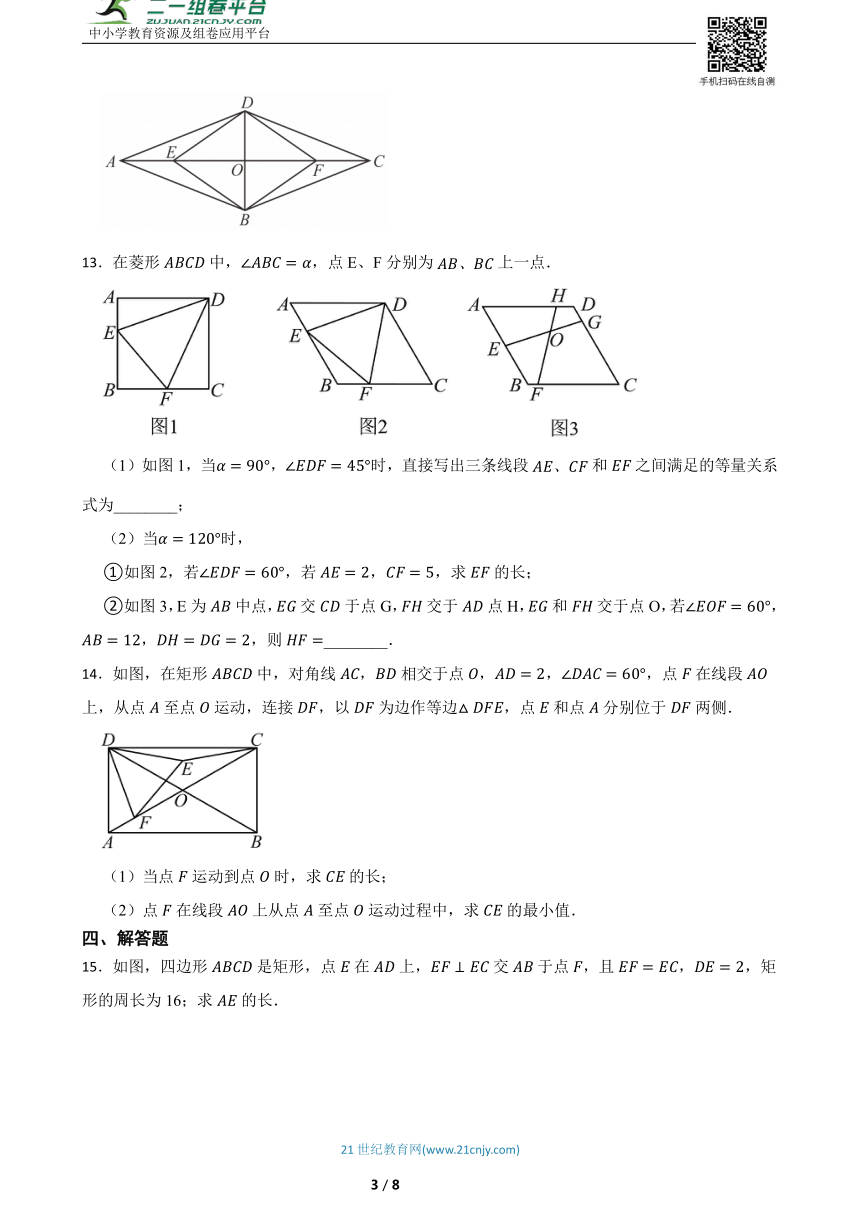
13.在菱形中,,点E、F分别为上一点.
(1)如图1,当,时,直接写出三条线段和之间满足的等量关系式为________;
(2)当时,
①如图2,若,若,,求的长;
②如图3,E为中点,交于点G,交于点H,和交于点O,若,,,则________.
14.如图,在矩形中,对角线,相交于点,,,点在线段上,从点至点运动,连接,以为边作等边,点和点分别位于两侧.
(1)当点运动到点时,求的长;
(2)点在线段上从点至点运动过程中,求的最小值.
四、解答题
15.如图,四边形是矩形,点在上,交于点,且,,矩形的周长为16;求的长.
五、作图题
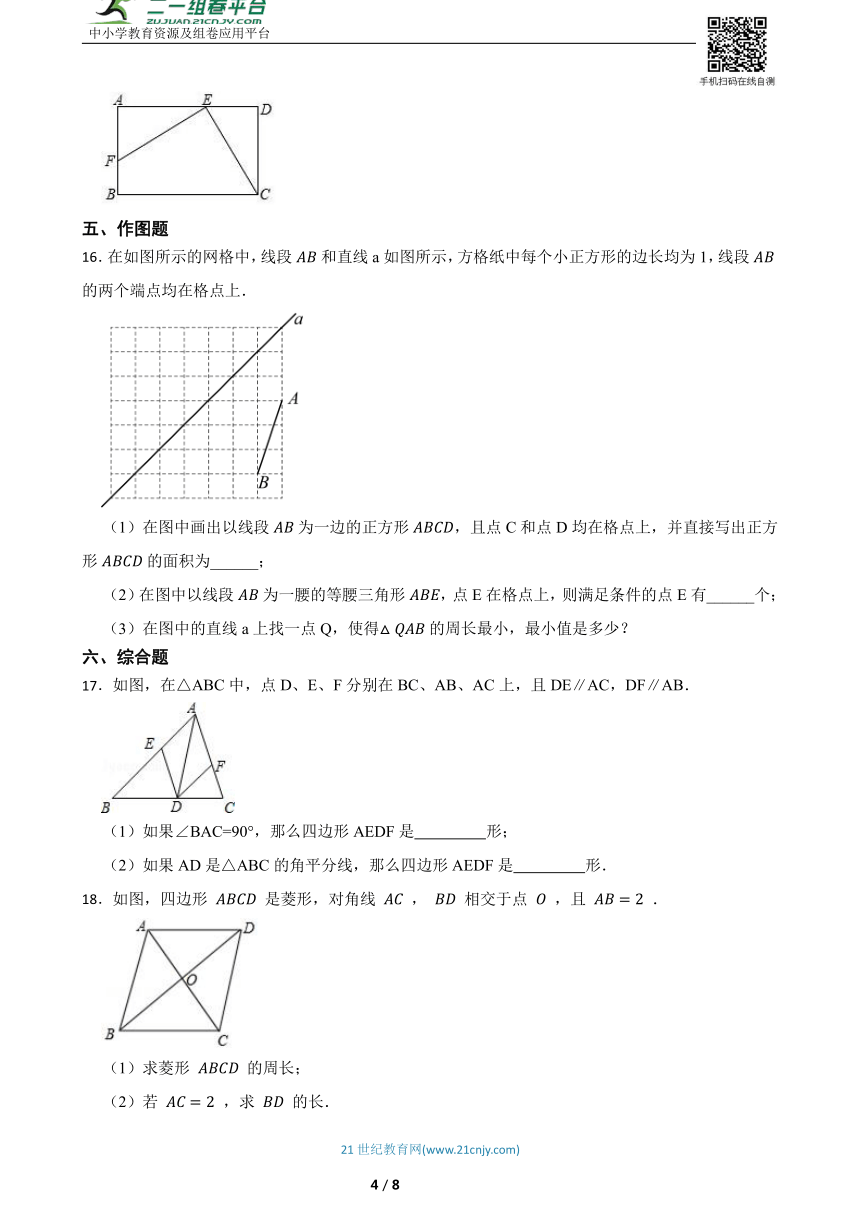
16.在如图所示的网格中,线段和直线a如图所示,方格纸中每个小正方形的边长均为1,线段的两个端点均在格点上.
(1)在图中画出以线段为一边的正方形,且点C和点D均在格点上,并直接写出正方形的面积为______;
(2)在图中以线段为一腰的等腰三角形,点E在格点上,则满足条件的点E有______个;
(3)在图中的直线a上找一点Q,使得的周长最小,最小值是多少?
六、综合题
17.如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
(1)如果∠BAC=90°,那么四边形AEDF是 形;
(2)如果AD是△ABC的角平分线,那么四边形AEDF是 形.
18.如图,四边形 是菱形,对角线 , 相交于点 ,且 .
(1)求菱形 的周长;
(2)若 ,求 的长.
19.如图,已知线段和线段.
(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)
①作线段的垂直平分线,交线段于点;
②以线段为对角线,作矩形,使得,并且点在线段的上方.
(2)当,时,求(1)中所作矩形的面积.
七、实践探究题
20.【问题背景】
如图,是一张等腰直角三角形纸板,,取、、中点进行第次剪取,记所得正方形面积为,如图,在余下的和中,分别剪取正方形,得到两个相同的正方形,称为第次剪取,并记这两个正方形面积和为如图.
【问题探究】
(1) ______ ;
(2)如图,再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第次剪取,并记这四个正方形面积和为继续操作下去,则第次剪取时, ______ ;第次剪取时, ______ .
【拓展延伸】
在第次剪取后,余下的所有小三角形的面积之和为______ .
答案解析部分
1.【答案】C
【知识点】坐标与图形性质;等腰三角形的判定;矩形的性质;正方形的性质
2.【答案】D
【知识点】菱形的性质;正方形的性质
3.【答案】B
【知识点】菱形的判定;矩形的判定;正方形的判定;真命题与假命题
4.【答案】B
【知识点】菱形的性质
5.【答案】C
【知识点】三角形全等及其性质;三角形全等的判定;勾股定理;正方形的性质
6.【答案】
【知识点】勾股定理;矩形的性质
7.【答案】
【知识点】菱形的性质
8.【答案】
【知识点】勾股定理;矩形的性质
9.【答案】
【知识点】勾股定理;菱形的性质
10.【答案】
【知识点】等腰三角形的性质;矩形的性质;内错角的概念
11.【答案】
【知识点】角平分线的性质;等腰三角形的判定与性质;勾股定理;正方形的性质
12.【答案】证明:四边形ABCD为菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AE=CF,
∴AO-AE=CO-CF,
∴EO=FO,
四边形EBFD是平行四边形,
又∵BD⊥AC,
四边形EBDF为菱形.
【知识点】平行四边形的判定;菱形的判定与性质
13.【答案】(1)
(2);
【知识点】等边三角形的判定与性质;勾股定理;正方形的性质
14.【答案】(1)2
(2)
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质;三角形全等的判定-SAS
15.【答案】3
【知识点】矩形的性质
16.【答案】(1)10
(2)6
(3)
【知识点】两点之间线段最短;等腰三角形的判定与性质;勾股定理;正方形的性质
17.【答案】(1)矩
(2)菱
【知识点】菱形的判定;矩形的判定
18.【答案】(1)解:∵四边形ABCD是菱形,AB=2,∴菱形ABCD的周长为:8
(2)解:∵四边形ABCD是菱形,AC=2,AB=2
∴AC⊥BD,AO=1,∴BO ,∴BD=2
【知识点】勾股定理;菱形的性质
19.【答案】(1)解:①线段的垂直平分线,如图所示,
②如图,矩形ABCD即为所求.
(2)解:如图所示,
∵在矩形中,,,,
∴在中,,
∴矩形的面积是,
【知识点】勾股定理;矩形的判定与性质;尺规作图-垂直平分线
20.【答案】(1);(2),;【拓展延伸】
【知识点】勾股定理;正方形的性质
21世纪教育网(www.21cnjy.com)
4 / 8
9.4矩形 ,菱形,正方形
一、单选题
1.将矩形纸片放置在如图所示的平面直角坐标系中,P为边上一动点(不与点B,C重合),连接,将折叠,得到.经过点P再次折叠纸片,使点B的对应点落在直线上,折痕交于点E.已知点,当四边形是正方形时,点E的坐标为( )
A. B. C. D.
2.下列是关于某个四边形的三个结论:①它是一个菱形;②它的对角线互相垂直;③它是一个正方形.下列推理过程正确的是( )
A.由①推出②,由②推出③ B.由②推出③,由③推出①
C.由③推出①,由①推出③ D.由③推出①,由①推出②
3.下列命题中是真命题的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线互相垂直且平分的四边形是菱形
C.有一个角是直角且对角线相等的四边形是矩形
D.一个角为且一组邻边相等的四边形是正方形
4.若菱形的两条对角线的长分别为6和10,则菱形的面积为( )
A.60 B.30 C.24 D.15
5.如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为(
A.8 B.9 C.10 D.11
二、填空题
6.如图,矩形中,,,是上的一个动点,于,于,则的值为 .
7.线段、为菱形的对角线,若,,则菱形的面积等于 .
8. 如图是办公桌摆件,四边形是矩形,若对角线,垂足是E,,,,则 .
9.已知在菱形中,,对角线与相交于点O,若,则该菱形的面积为 .(结果保留根号)
10.如图,在矩形中,已知,则的度数为 °.
11.如图,在正方形中,是对角线,平分交于点,若,则的长为 .
三、计算题
12.如图,在菱形中,交于点,点在上,求证:四边形是菱形.
13.在菱形中,,点E、F分别为上一点.
(1)如图1,当,时,直接写出三条线段和之间满足的等量关系式为________;
(2)当时,
①如图2,若,若,,求的长;
②如图3,E为中点,交于点G,交于点H,和交于点O,若,,,则________.
14.如图,在矩形中,对角线,相交于点,,,点在线段上,从点至点运动,连接,以为边作等边,点和点分别位于两侧.
(1)当点运动到点时,求的长;
(2)点在线段上从点至点运动过程中,求的最小值.
四、解答题
15.如图,四边形是矩形,点在上,交于点,且,,矩形的周长为16;求的长.
五、作图题
16.在如图所示的网格中,线段和直线a如图所示,方格纸中每个小正方形的边长均为1,线段的两个端点均在格点上.
(1)在图中画出以线段为一边的正方形,且点C和点D均在格点上,并直接写出正方形的面积为______;
(2)在图中以线段为一腰的等腰三角形,点E在格点上,则满足条件的点E有______个;
(3)在图中的直线a上找一点Q,使得的周长最小,最小值是多少?
六、综合题
17.如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
(1)如果∠BAC=90°,那么四边形AEDF是 形;
(2)如果AD是△ABC的角平分线,那么四边形AEDF是 形.
18.如图,四边形 是菱形,对角线 , 相交于点 ,且 .
(1)求菱形 的周长;
(2)若 ,求 的长.
19.如图,已知线段和线段.
(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)
①作线段的垂直平分线,交线段于点;
②以线段为对角线,作矩形,使得,并且点在线段的上方.
(2)当,时,求(1)中所作矩形的面积.
七、实践探究题
20.【问题背景】
如图,是一张等腰直角三角形纸板,,取、、中点进行第次剪取,记所得正方形面积为,如图,在余下的和中,分别剪取正方形,得到两个相同的正方形,称为第次剪取,并记这两个正方形面积和为如图.
【问题探究】
(1) ______ ;
(2)如图,再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第次剪取,并记这四个正方形面积和为继续操作下去,则第次剪取时, ______ ;第次剪取时, ______ .
【拓展延伸】
在第次剪取后,余下的所有小三角形的面积之和为______ .
答案解析部分
1.【答案】C
【知识点】坐标与图形性质;等腰三角形的判定;矩形的性质;正方形的性质
2.【答案】D
【知识点】菱形的性质;正方形的性质
3.【答案】B
【知识点】菱形的判定;矩形的判定;正方形的判定;真命题与假命题
4.【答案】B
【知识点】菱形的性质
5.【答案】C
【知识点】三角形全等及其性质;三角形全等的判定;勾股定理;正方形的性质
6.【答案】
【知识点】勾股定理;矩形的性质
7.【答案】
【知识点】菱形的性质
8.【答案】
【知识点】勾股定理;矩形的性质
9.【答案】
【知识点】勾股定理;菱形的性质
10.【答案】
【知识点】等腰三角形的性质;矩形的性质;内错角的概念
11.【答案】
【知识点】角平分线的性质;等腰三角形的判定与性质;勾股定理;正方形的性质
12.【答案】证明:四边形ABCD为菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AE=CF,
∴AO-AE=CO-CF,
∴EO=FO,
四边形EBFD是平行四边形,
又∵BD⊥AC,
四边形EBDF为菱形.
【知识点】平行四边形的判定;菱形的判定与性质
13.【答案】(1)
(2);
【知识点】等边三角形的判定与性质;勾股定理;正方形的性质
14.【答案】(1)2
(2)
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质;三角形全等的判定-SAS
15.【答案】3
【知识点】矩形的性质
16.【答案】(1)10
(2)6
(3)
【知识点】两点之间线段最短;等腰三角形的判定与性质;勾股定理;正方形的性质
17.【答案】(1)矩
(2)菱
【知识点】菱形的判定;矩形的判定
18.【答案】(1)解:∵四边形ABCD是菱形,AB=2,∴菱形ABCD的周长为:8
(2)解:∵四边形ABCD是菱形,AC=2,AB=2
∴AC⊥BD,AO=1,∴BO ,∴BD=2
【知识点】勾股定理;菱形的性质
19.【答案】(1)解:①线段的垂直平分线,如图所示,
②如图,矩形ABCD即为所求.
(2)解:如图所示,
∵在矩形中,,,,
∴在中,,
∴矩形的面积是,
【知识点】勾股定理;矩形的判定与性质;尺规作图-垂直平分线
20.【答案】(1);(2),;【拓展延伸】
【知识点】勾股定理;正方形的性质
21世纪教育网(www.21cnjy.com)
4 / 8
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
