第九章 中心对称图形-----平行四边形 章末练习(含答案)
文档属性
| 名称 | 第九章 中心对称图形-----平行四边形 章末练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 544.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 04:36:56 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 中心对称图形-----平行四边形
一、单选题
1.下列中国传统纹样的图案是中心对称图形的是( )
A. B. C. D.
2.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若,,则菱形ABCD的边长为( )
A.2 B.2.5 C.3 D.5
3.菱形的两条对角线长分别为和,则它的高为( )
A. B. C. D.
4.如图,在四边形中,,,点E,F在对角线上,连接,则添加下列条件,仍不能判断四边形是平行四边形的是( )
A. B.
C. D.,
5.两条对角线互相垂直平分的四边形是( )
A.等腰梯形 B.菱形 C.矩形 D.平行四边形
6.已知平行四边形一边长为5,一条对角线长为6,则它的另一条对角线α的取值范围为( )
A.1<α<11 B.4<α<16
C.10<α<12 D.以上答案都错误
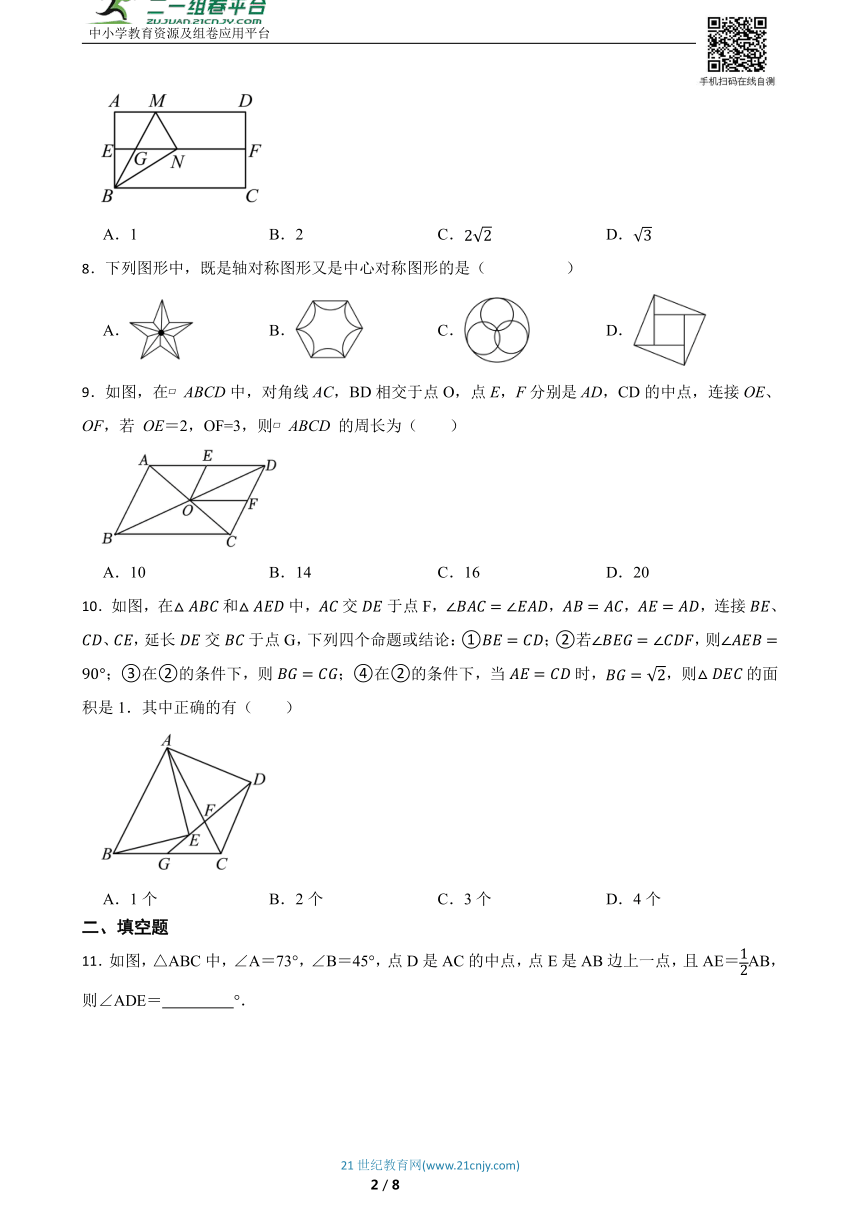
7.如图,对折矩形纸片,使与重合,得到折痕,把纸片展平,再一次折叠纸片,使点落在上,并使折痕经过点,得到折痕,同时得到线段.若与交点为,,则( )
A.1 B.2 C. D.
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
9.如图,在 ABCD中,对角线AC,BD相交于点O,点E,F分别是AD,CD的中点,连接OE、OF,若 OE=2,OF=3,则 ABCD 的周长为( )
A.10 B.14 C.16 D.20
10.如图,在和中,交于点F,,,,连接、、,延长交于点G,下列四个命题或结论:①;②若,则;③在②的条件下,则;④在②的条件下,当时,,则的面积是1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,△ABC中,∠A=73°,∠B=45°,点D是AC的中点,点E是AB边上一点,且AE=AB,则∠ADE= °.
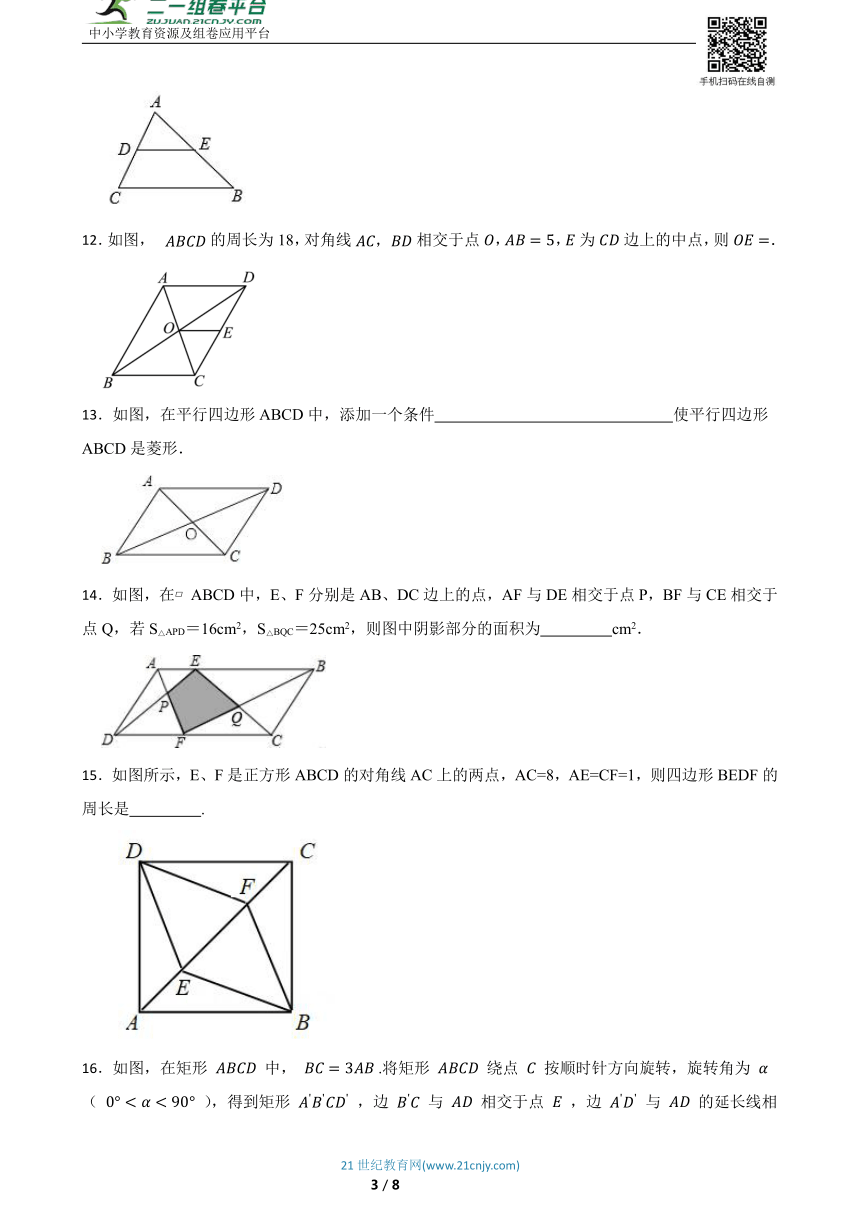
12.如图,的周长为18,对角线相交于点,,为边上的中点,则.
13.如图,在平行四边形ABCD中,添加一个条件 使平行四边形ABCD是菱形.
14.如图,在 ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为 cm2.
15.如图所示,E、F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=1,则四边形BEDF的周长是 .
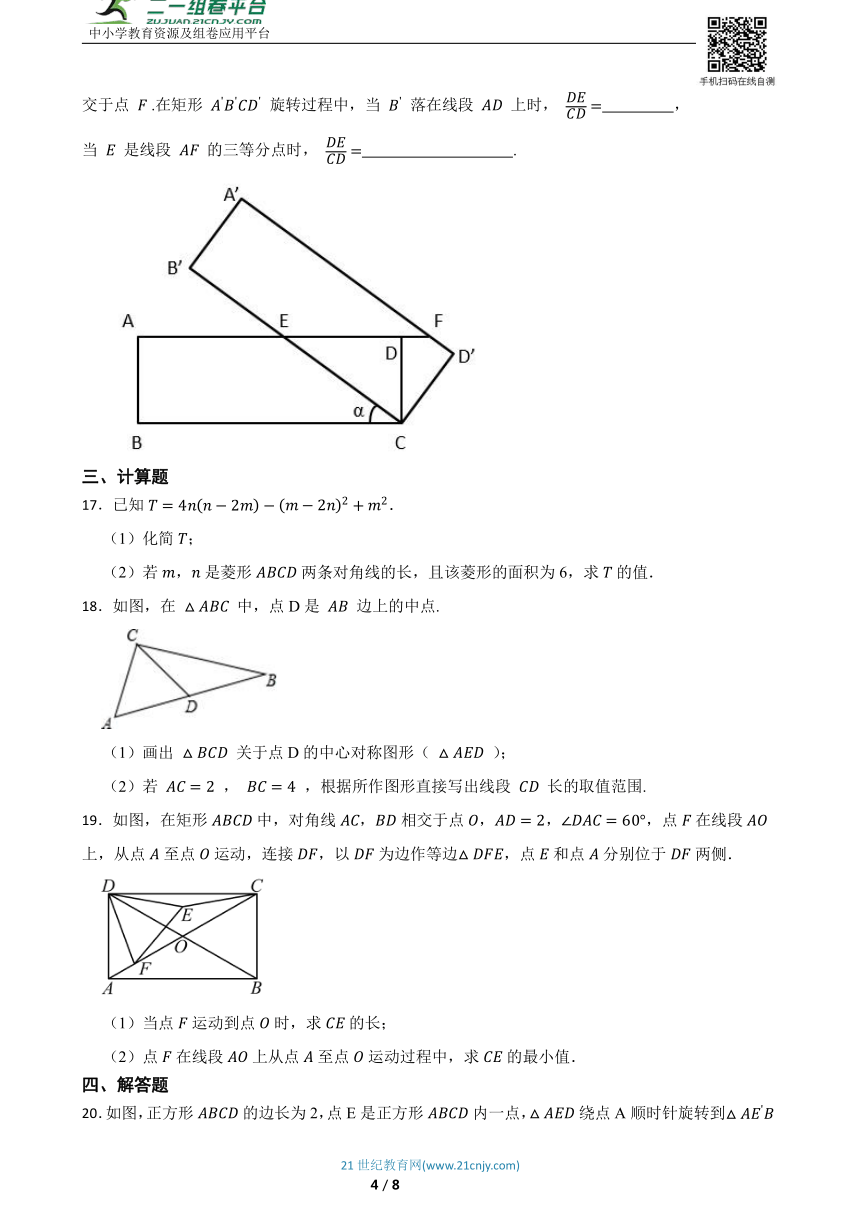
16.如图,在矩形 中, .将矩形 绕点 按顺时针方向旋转,旋转角为 ( ),得到矩形 ,边 与 相交于点 ,边 与 的延长线相交于点 .在矩形 旋转过程中,当 落在线段 上时, ,当 是线段 的三等分点时, .
三、计算题
17.已知.
(1)化简;
(2)若,是菱形两条对角线的长,且该菱形的面积为6,求的值.
18.如图,在 中,点D是 边上的中点.
(1)画出 关于点D的中心对称图形( );
(2)若 , ,根据所作图形直接写出线段 长的取值范围.
19.如图,在矩形中,对角线,相交于点,,,点在线段上,从点至点运动,连接,以为边作等边,点和点分别位于两侧.
(1)当点运动到点时,求的长;
(2)点在线段上从点至点运动过程中,求的最小值.
四、解答题
20.如图,正方形的边长为2,点E是正方形内一点,绕点A顺时针旋转到的位置,点E的对应点是点,点D的对应点是点B.
(1)绕点A顺时针旋转到的位置,旋转角是多少度?
(2)若,,求线段的长.
21.用反证法证明:若两条直线a、b相交,则只有一个交点。
22.如图所示,四边形 是张大爷的一块小菜地,已知 , , , ,请帮张大爷计算一下这个四边形菜地的周长.
23.如图1,在平面直角坐标系中,为坐标原点,抛物线与轴交于点A、(A左右),与轴交于点,直线经过点、.
(1)求抛物线的解析式;
(2)如图2,点为第一象限内抛物线上一点,连接,,设点的横坐标为,的面积为,求与之间的函数关系式(不要求写出自变量的取值范围);
(3)在(2)的条件下,如图3,交轴于点,,点为轴上点右侧一点,,将线段绕着点逆时针旋转至,,连接交抛物线于点,求点的坐标.
答案解析部分
1.【答案】C
【知识点】中心对称及中心对称图形
2.【答案】D
【知识点】勾股定理;菱形的判定与性质;三角形的中位线定理
3.【答案】A
【知识点】勾股定理;菱形的性质
4.【答案】C
【知识点】三角形全等及其性质;平行四边形的判定与性质
5.【答案】B
【知识点】菱形的判定
6.【答案】B
【知识点】三角形三边关系;平行四边形的性质
7.【答案】B
【知识点】平行线的判定与性质;矩形的性质
8.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
9.【答案】D
【知识点】平行四边形的性质;三角形的中位线定理
10.【答案】D
【知识点】三角形全等的判定;等腰三角形的判定与性质;勾股定理;平行四边形的判定与性质
11.【答案】62
【知识点】三角形内角和定理;三角形的中位线定理
12.【答案】2
【知识点】平行四边形的性质;三角形的中位线定理
13.【答案】AB=BC(或AC⊥BD)答案不唯一
【知识点】菱形的判定
14.【答案】41
【知识点】平行四边形的性质
15.【答案】20
【知识点】勾股定理;菱形的判定与性质;正方形的性质
16.【答案】; 或
【知识点】三角形的面积;勾股定理;矩形的性质;旋转的性质
17.【答案】(1)
(2)
【知识点】整式的混合运算;菱形的性质
18.【答案】(1)解:所画图形,如图所示:
沿长CD至点E,使DE=CD,连接AE,则 就是所作的图形,
(2)
【知识点】三角形三边关系;中心对称及中心对称图形
19.【答案】(1)2
(2)
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质;三角形全等的判定-SAS
20.【答案】(1)
(2)
【知识点】勾股定理;正方形的性质;旋转的性质
21.【答案】解:假设直线a、b不止有一个公共点,则至少有两个公共点,不妨设为A、B,即直线a、b同时过点A、B,也就是说过A、B两点可以作两条直线a、b,这和公理“过两点能且只能作一条直线”相矛盾,所以假设不成立,两条直线相交只有一个交点。
【知识点】反证法
22.【答案】解:如图,作 于 .
, ,
,
四边形 是矩形,
, ,
在 中, ,
,
四边形 的周长 .
【知识点】勾股定理;矩形的判定与性质
23.【答案】(1)
(2)
(3)
【知识点】勾股定理;旋转的性质
21世纪教育网(www.21cnjy.com)
3 / 8
第九章 中心对称图形-----平行四边形
一、单选题
1.下列中国传统纹样的图案是中心对称图形的是( )
A. B. C. D.
2.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若,,则菱形ABCD的边长为( )
A.2 B.2.5 C.3 D.5
3.菱形的两条对角线长分别为和,则它的高为( )
A. B. C. D.
4.如图,在四边形中,,,点E,F在对角线上,连接,则添加下列条件,仍不能判断四边形是平行四边形的是( )
A. B.
C. D.,
5.两条对角线互相垂直平分的四边形是( )
A.等腰梯形 B.菱形 C.矩形 D.平行四边形
6.已知平行四边形一边长为5,一条对角线长为6,则它的另一条对角线α的取值范围为( )
A.1<α<11 B.4<α<16
C.10<α<12 D.以上答案都错误
7.如图,对折矩形纸片,使与重合,得到折痕,把纸片展平,再一次折叠纸片,使点落在上,并使折痕经过点,得到折痕,同时得到线段.若与交点为,,则( )
A.1 B.2 C. D.
8.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
9.如图,在 ABCD中,对角线AC,BD相交于点O,点E,F分别是AD,CD的中点,连接OE、OF,若 OE=2,OF=3,则 ABCD 的周长为( )
A.10 B.14 C.16 D.20
10.如图,在和中,交于点F,,,,连接、、,延长交于点G,下列四个命题或结论:①;②若,则;③在②的条件下,则;④在②的条件下,当时,,则的面积是1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,△ABC中,∠A=73°,∠B=45°,点D是AC的中点,点E是AB边上一点,且AE=AB,则∠ADE= °.
12.如图,的周长为18,对角线相交于点,,为边上的中点,则.
13.如图,在平行四边形ABCD中,添加一个条件 使平行四边形ABCD是菱形.
14.如图,在 ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC=25cm2,则图中阴影部分的面积为 cm2.
15.如图所示,E、F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=1,则四边形BEDF的周长是 .
16.如图,在矩形 中, .将矩形 绕点 按顺时针方向旋转,旋转角为 ( ),得到矩形 ,边 与 相交于点 ,边 与 的延长线相交于点 .在矩形 旋转过程中,当 落在线段 上时, ,当 是线段 的三等分点时, .
三、计算题
17.已知.
(1)化简;
(2)若,是菱形两条对角线的长,且该菱形的面积为6,求的值.
18.如图,在 中,点D是 边上的中点.
(1)画出 关于点D的中心对称图形( );
(2)若 , ,根据所作图形直接写出线段 长的取值范围.
19.如图,在矩形中,对角线,相交于点,,,点在线段上,从点至点运动,连接,以为边作等边,点和点分别位于两侧.
(1)当点运动到点时,求的长;
(2)点在线段上从点至点运动过程中,求的最小值.
四、解答题
20.如图,正方形的边长为2,点E是正方形内一点,绕点A顺时针旋转到的位置,点E的对应点是点,点D的对应点是点B.
(1)绕点A顺时针旋转到的位置,旋转角是多少度?
(2)若,,求线段的长.
21.用反证法证明:若两条直线a、b相交,则只有一个交点。
22.如图所示,四边形 是张大爷的一块小菜地,已知 , , , ,请帮张大爷计算一下这个四边形菜地的周长.
23.如图1,在平面直角坐标系中,为坐标原点,抛物线与轴交于点A、(A左右),与轴交于点,直线经过点、.
(1)求抛物线的解析式;
(2)如图2,点为第一象限内抛物线上一点,连接,,设点的横坐标为,的面积为,求与之间的函数关系式(不要求写出自变量的取值范围);
(3)在(2)的条件下,如图3,交轴于点,,点为轴上点右侧一点,,将线段绕着点逆时针旋转至,,连接交抛物线于点,求点的坐标.
答案解析部分
1.【答案】C
【知识点】中心对称及中心对称图形
2.【答案】D
【知识点】勾股定理;菱形的判定与性质;三角形的中位线定理
3.【答案】A
【知识点】勾股定理;菱形的性质
4.【答案】C
【知识点】三角形全等及其性质;平行四边形的判定与性质
5.【答案】B
【知识点】菱形的判定
6.【答案】B
【知识点】三角形三边关系;平行四边形的性质
7.【答案】B
【知识点】平行线的判定与性质;矩形的性质
8.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
9.【答案】D
【知识点】平行四边形的性质;三角形的中位线定理
10.【答案】D
【知识点】三角形全等的判定;等腰三角形的判定与性质;勾股定理;平行四边形的判定与性质
11.【答案】62
【知识点】三角形内角和定理;三角形的中位线定理
12.【答案】2
【知识点】平行四边形的性质;三角形的中位线定理
13.【答案】AB=BC(或AC⊥BD)答案不唯一
【知识点】菱形的判定
14.【答案】41
【知识点】平行四边形的性质
15.【答案】20
【知识点】勾股定理;菱形的判定与性质;正方形的性质
16.【答案】; 或
【知识点】三角形的面积;勾股定理;矩形的性质;旋转的性质
17.【答案】(1)
(2)
【知识点】整式的混合运算;菱形的性质
18.【答案】(1)解:所画图形,如图所示:
沿长CD至点E,使DE=CD,连接AE,则 就是所作的图形,
(2)
【知识点】三角形三边关系;中心对称及中心对称图形
19.【答案】(1)2
(2)
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质;三角形全等的判定-SAS
20.【答案】(1)
(2)
【知识点】勾股定理;正方形的性质;旋转的性质
21.【答案】解:假设直线a、b不止有一个公共点,则至少有两个公共点,不妨设为A、B,即直线a、b同时过点A、B,也就是说过A、B两点可以作两条直线a、b,这和公理“过两点能且只能作一条直线”相矛盾,所以假设不成立,两条直线相交只有一个交点。
【知识点】反证法
22.【答案】解:如图,作 于 .
, ,
,
四边形 是矩形,
, ,
在 中, ,
,
四边形 的周长 .
【知识点】勾股定理;矩形的判定与性质
23.【答案】(1)
(2)
(3)
【知识点】勾股定理;旋转的性质
21世纪教育网(www.21cnjy.com)
3 / 8
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
