第九章 中心对称图形-----平行四边形 章末练习【培优】(含答案)
文档属性
| 名称 | 第九章 中心对称图形-----平行四边形 章末练习【培优】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 794.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 04:37:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 中心对称图形-----平行四边形【培优】
一、单选题
1.(2024九上·北京市月考)北京城区的胡同中很多精美的砖雕美化了生活环境,砖雕形状的设计采用了丰富多彩的图案.下列砖雕图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(2024九下·民勤模拟)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若,,则菱形ABCD的边长为( )
A.2 B.2.5 C.3 D.5
3.(2024八下·邳州期中)已知:在菱形中,,,则的长为( )
A.2 B. C. D.
4.(2024八下·巴彦期末)如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是
A.4 B.3 C.2 D.1
5.(2024九上·北京市开学考)下列命题中是真命题的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线互相垂直且平分的四边形是菱形
C.有一个角是直角且对角线相等的四边形是矩形
D.一个角为且一组邻边相等的四边形是正方形
6.(2024八下·绵阳月考)如图,在平行四边形中,对角线、相交于点,如果,,,设,那么的取值范围是( )
A. B. C. D.
7.(2023七下·上杭期末)如图,将长方形纸片沿折叠(折线交于E,交于F),点C、D分别落在点、,交于G,再将四边形沿折叠,点、的落点分别是分别落在点、,交于H.下列四个结论:①;②;③;④.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
8.(2024九下·广西壮族自治区模拟)下列几何图形中,既是轴对称图形,又是中心对称图形的是( )
A.线段 B.等边三角形 C.平行四边形 D.正五边形
9.(2024八下·长沙期末)如图,在平行四边形中,,为上一动点,,分别为,的中点,则的长为( )
A.3 B.3.5 C.4 D.4.5
10.(2024八下·广州期末)如图,在和中,交于点F,,,,连接、、,延长交于点G,下列四个命题或结论:①;②若,则;③在②的条件下,则;④在②的条件下,当时,,则的面积是1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2024九下·乌鲁木齐模拟)如图,△ABC中,∠A=73°,∠B=45°,点D是AC的中点,点E是AB边上一点,且AE=AB,则∠ADE= °.
12.(2023八下·西城期中)如图,的对角线,相交于点,点,分别是线段,的中点,若,的周长是,则 cm.
13.(2024八下·确山期中)如图,已知正方形,点M是边延长线上的动点(不与点A重合)且,由平移得到,若过点E作,H为垂足,则有以下结论:
①点M位置变化,使得时,;
②无论点M运动到何处,都有;
③在点M的运动过程中,四边形可能成为菱形;
④无论点M运动到何处,一定大于.
以上结论正确的有 (把所有正确结论的序号都填上).
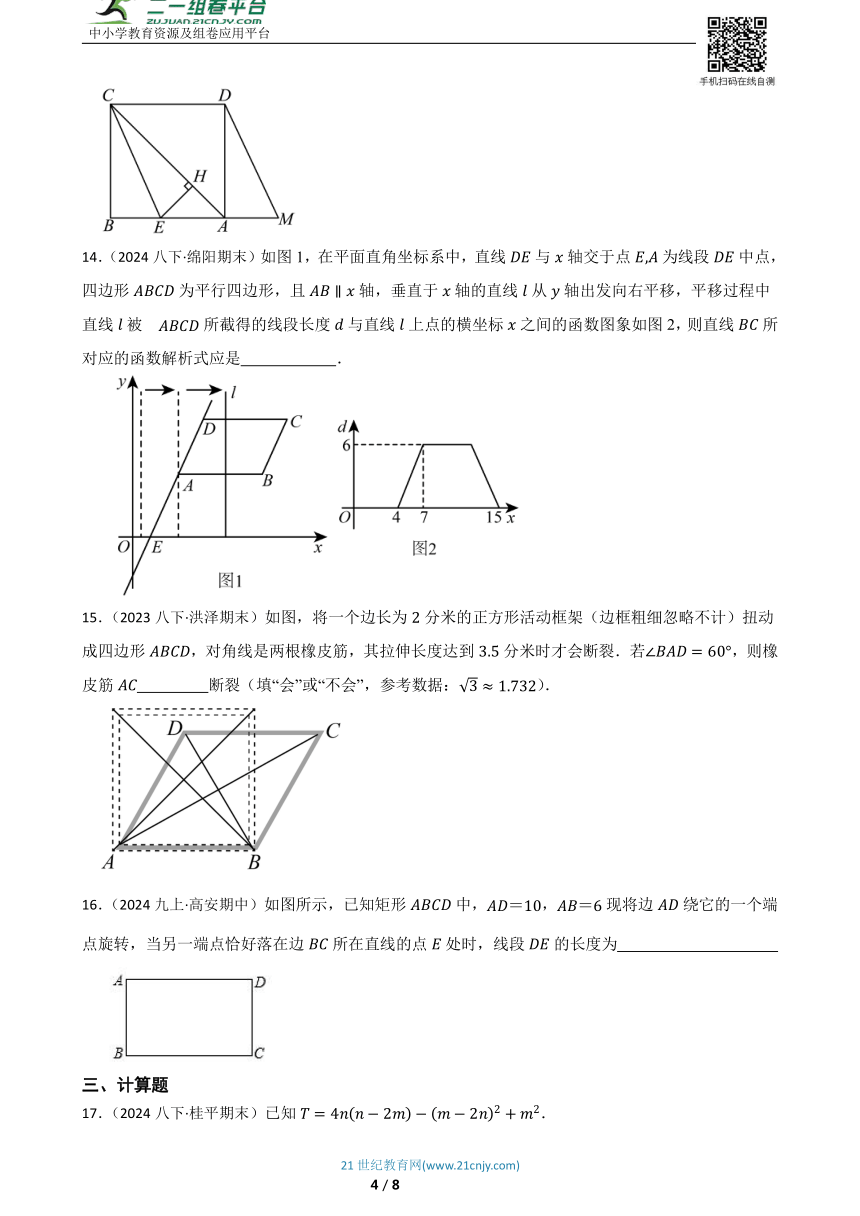
14.(2024八下·绵阳期末)如图1,在平面直角坐标系中,直线与轴交于点为线段中点,四边形为平行四边形,且轴,垂直于轴的直线从轴出发向右平移,平移过程中直线被所截得的线段长度与直线上点的横坐标之间的函数图象如图2,则直线所对应的函数解析式应是 .
15.(2023八下·洪泽期末)如图,将一个边长为分米的正方形活动框架(边框粗细忽略不计)扭动成四边形,对角线是两根橡皮筋,其拉伸长度达到分米时才会断裂.若,则橡皮筋 断裂(填“会”或“不会”,参考数据:).
16.(2024九上·高安期中)如图所示,已知矩形中,,现将边绕它的一个端点旋转,当另一端点恰好落在边所在直线的点处时,线段的长度为
三、计算题
17.(2024八下·桂平期末)已知.
(1)化简;
(2)若,是菱形两条对角线的长,且该菱形的面积为6,求的值.
18.(2024八上·陇西期末)一个等腰三角形的两边长a和 b满足,且.
(1)请你求出a和b的值.
(2)求这个等腰三角形的周长.
19.(2024八下·新吴期末)如图,在矩形中,对角线,相交于点,,,点在线段上,从点至点运动,连接,以为边作等边,点和点分别位于两侧.
(1)当点运动到点时,求的长;
(2)点在线段上从点至点运动过程中,求的最小值.
四、解答题
20.(2024九上·榕江期中)如图,正方形的边长为2,点E是正方形内一点,绕点A顺时针旋转到的位置,点E的对应点是点,点D的对应点是点B.
(1)绕点A顺时针旋转到的位置,旋转角是多少度?
(2)若,,求线段的长.
21.用反证法证明: 等腰三角形 的底角 和 必定是锐角.
22.(2024八下·新乡月考)请利用勾股定理解决下列问题.
(1)如图1,在中,,,,请求出边上高的长度h;
(2)如图2,在梯形中,,,,,,求和之间高的长度x.(提示:作于点,于点 ,则四边形为矩形)
23.(2023九上·蓬江期中)如图,是正方形的边上一点,过点A作交的延长线于点,连接.
(1)可以由顺时针旋转得到,则旋转中心是 ,旋转角是 度.
(2)试说明的形状.
(3)若,,求的长.
答案解析部分
1.【答案】A
【知识点】轴对称图形;中心对称及中心对称图形
2.【答案】D
【知识点】勾股定理;菱形的判定与性质;三角形的中位线定理
3.【答案】D
【知识点】含30°角的直角三角形;勾股定理;菱形的性质
4.【答案】B
【知识点】三角形全等及其性质;平行四边形的判定与性质
5.【答案】B
【知识点】菱形的判定;矩形的判定;正方形的判定;真命题与假命题
6.【答案】C
【知识点】三角形三边关系;平行四边形的性质
7.【答案】C
【知识点】平行线的判定与性质;矩形的性质
8.【答案】A
【知识点】轴对称图形;中心对称及中心对称图形
9.【答案】B
【知识点】平行四边形的性质;三角形的中位线定理
10.【答案】D
【知识点】三角形全等的判定;等腰三角形的判定与性质;勾股定理;平行四边形的判定与性质
11.【答案】62
【知识点】三角形内角和定理;三角形的中位线定理
12.【答案】
【知识点】平行四边形的性质;三角形的中位线定理
13.【答案】①②④
【知识点】含30°角的直角三角形;勾股定理;菱形的判定;正方形的性质
14.【答案】
【知识点】待定系数法求一次函数解析式;平行四边形的性质;一次函数的实际应用-几何问题
15.【答案】不会
【知识点】含30°角的直角三角形;勾股定理;菱形的判定与性质;正方形的性质
16.【答案】或或
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质;旋转的性质
17.【答案】(1)
(2)
【知识点】整式的混合运算;菱形的性质
18.【答案】(1),;
(2)等腰三角形的周长是16.
【知识点】平方差公式及应用;三角形三边关系;加减消元法解二元一次方程组;等腰三角形的概念
19.【答案】(1)2
(2)
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质;三角形全等的判定-SAS
20.【答案】(1)
(2)
【知识点】勾股定理;正方形的性质;旋转的性质
21.【答案】证明:假设等腰△ABC的底角∠B与∠C都不是锐角,
则∠B=∠C≥90°,
∴∠B+∠C≥180°,
∴∠A+∠B+∠C>180°,这与三角形内角和等于180°矛盾,
∴假设错误,
∴等腰△ABC的底角∠B与∠C都是锐角.
【知识点】三角形内角和定理;等腰三角形的性质;反证法
22.【答案】(1)
(2)
【知识点】勾股定理;勾股定理的逆定理;矩形的判定与性质
23.【答案】(1)点A,
(2)是等腰直角三角形
(3)
【知识点】直角三角形全等的判定-HL;勾股定理;正方形的性质;旋转的性质
21世纪教育网(www.21cnjy.com)
4 / 8
第九章 中心对称图形-----平行四边形【培优】
一、单选题
1.(2024九上·北京市月考)北京城区的胡同中很多精美的砖雕美化了生活环境,砖雕形状的设计采用了丰富多彩的图案.下列砖雕图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(2024九下·民勤模拟)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,若,,则菱形ABCD的边长为( )
A.2 B.2.5 C.3 D.5
3.(2024八下·邳州期中)已知:在菱形中,,,则的长为( )
A.2 B. C. D.
4.(2024八下·巴彦期末)如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是
A.4 B.3 C.2 D.1
5.(2024九上·北京市开学考)下列命题中是真命题的是( )
A.一组对边相等,另一组对边平行的四边形是平行四边形
B.对角线互相垂直且平分的四边形是菱形
C.有一个角是直角且对角线相等的四边形是矩形
D.一个角为且一组邻边相等的四边形是正方形
6.(2024八下·绵阳月考)如图,在平行四边形中,对角线、相交于点,如果,,,设,那么的取值范围是( )
A. B. C. D.
7.(2023七下·上杭期末)如图,将长方形纸片沿折叠(折线交于E,交于F),点C、D分别落在点、,交于G,再将四边形沿折叠,点、的落点分别是分别落在点、,交于H.下列四个结论:①;②;③;④.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
8.(2024九下·广西壮族自治区模拟)下列几何图形中,既是轴对称图形,又是中心对称图形的是( )
A.线段 B.等边三角形 C.平行四边形 D.正五边形
9.(2024八下·长沙期末)如图,在平行四边形中,,为上一动点,,分别为,的中点,则的长为( )
A.3 B.3.5 C.4 D.4.5
10.(2024八下·广州期末)如图,在和中,交于点F,,,,连接、、,延长交于点G,下列四个命题或结论:①;②若,则;③在②的条件下,则;④在②的条件下,当时,,则的面积是1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2024九下·乌鲁木齐模拟)如图,△ABC中,∠A=73°,∠B=45°,点D是AC的中点,点E是AB边上一点,且AE=AB,则∠ADE= °.
12.(2023八下·西城期中)如图,的对角线,相交于点,点,分别是线段,的中点,若,的周长是,则 cm.
13.(2024八下·确山期中)如图,已知正方形,点M是边延长线上的动点(不与点A重合)且,由平移得到,若过点E作,H为垂足,则有以下结论:
①点M位置变化,使得时,;
②无论点M运动到何处,都有;
③在点M的运动过程中,四边形可能成为菱形;
④无论点M运动到何处,一定大于.
以上结论正确的有 (把所有正确结论的序号都填上).
14.(2024八下·绵阳期末)如图1,在平面直角坐标系中,直线与轴交于点为线段中点,四边形为平行四边形,且轴,垂直于轴的直线从轴出发向右平移,平移过程中直线被所截得的线段长度与直线上点的横坐标之间的函数图象如图2,则直线所对应的函数解析式应是 .
15.(2023八下·洪泽期末)如图,将一个边长为分米的正方形活动框架(边框粗细忽略不计)扭动成四边形,对角线是两根橡皮筋,其拉伸长度达到分米时才会断裂.若,则橡皮筋 断裂(填“会”或“不会”,参考数据:).
16.(2024九上·高安期中)如图所示,已知矩形中,,现将边绕它的一个端点旋转,当另一端点恰好落在边所在直线的点处时,线段的长度为
三、计算题
17.(2024八下·桂平期末)已知.
(1)化简;
(2)若,是菱形两条对角线的长,且该菱形的面积为6,求的值.
18.(2024八上·陇西期末)一个等腰三角形的两边长a和 b满足,且.
(1)请你求出a和b的值.
(2)求这个等腰三角形的周长.
19.(2024八下·新吴期末)如图,在矩形中,对角线,相交于点,,,点在线段上,从点至点运动,连接,以为边作等边,点和点分别位于两侧.
(1)当点运动到点时,求的长;
(2)点在线段上从点至点运动过程中,求的最小值.
四、解答题
20.(2024九上·榕江期中)如图,正方形的边长为2,点E是正方形内一点,绕点A顺时针旋转到的位置,点E的对应点是点,点D的对应点是点B.
(1)绕点A顺时针旋转到的位置,旋转角是多少度?
(2)若,,求线段的长.
21.用反证法证明: 等腰三角形 的底角 和 必定是锐角.
22.(2024八下·新乡月考)请利用勾股定理解决下列问题.
(1)如图1,在中,,,,请求出边上高的长度h;
(2)如图2,在梯形中,,,,,,求和之间高的长度x.(提示:作于点,于点 ,则四边形为矩形)
23.(2023九上·蓬江期中)如图,是正方形的边上一点,过点A作交的延长线于点,连接.
(1)可以由顺时针旋转得到,则旋转中心是 ,旋转角是 度.
(2)试说明的形状.
(3)若,,求的长.
答案解析部分
1.【答案】A
【知识点】轴对称图形;中心对称及中心对称图形
2.【答案】D
【知识点】勾股定理;菱形的判定与性质;三角形的中位线定理
3.【答案】D
【知识点】含30°角的直角三角形;勾股定理;菱形的性质
4.【答案】B
【知识点】三角形全等及其性质;平行四边形的判定与性质
5.【答案】B
【知识点】菱形的判定;矩形的判定;正方形的判定;真命题与假命题
6.【答案】C
【知识点】三角形三边关系;平行四边形的性质
7.【答案】C
【知识点】平行线的判定与性质;矩形的性质
8.【答案】A
【知识点】轴对称图形;中心对称及中心对称图形
9.【答案】B
【知识点】平行四边形的性质;三角形的中位线定理
10.【答案】D
【知识点】三角形全等的判定;等腰三角形的判定与性质;勾股定理;平行四边形的判定与性质
11.【答案】62
【知识点】三角形内角和定理;三角形的中位线定理
12.【答案】
【知识点】平行四边形的性质;三角形的中位线定理
13.【答案】①②④
【知识点】含30°角的直角三角形;勾股定理;菱形的判定;正方形的性质
14.【答案】
【知识点】待定系数法求一次函数解析式;平行四边形的性质;一次函数的实际应用-几何问题
15.【答案】不会
【知识点】含30°角的直角三角形;勾股定理;菱形的判定与性质;正方形的性质
16.【答案】或或
【知识点】等腰三角形的判定与性质;勾股定理;矩形的性质;旋转的性质
17.【答案】(1)
(2)
【知识点】整式的混合运算;菱形的性质
18.【答案】(1),;
(2)等腰三角形的周长是16.
【知识点】平方差公式及应用;三角形三边关系;加减消元法解二元一次方程组;等腰三角形的概念
19.【答案】(1)2
(2)
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质;三角形全等的判定-SAS
20.【答案】(1)
(2)
【知识点】勾股定理;正方形的性质;旋转的性质
21.【答案】证明:假设等腰△ABC的底角∠B与∠C都不是锐角,
则∠B=∠C≥90°,
∴∠B+∠C≥180°,
∴∠A+∠B+∠C>180°,这与三角形内角和等于180°矛盾,
∴假设错误,
∴等腰△ABC的底角∠B与∠C都是锐角.
【知识点】三角形内角和定理;等腰三角形的性质;反证法
22.【答案】(1)
(2)
【知识点】勾股定理;勾股定理的逆定理;矩形的判定与性质
23.【答案】(1)点A,
(2)是等腰直角三角形
(3)
【知识点】直角三角形全等的判定-HL;勾股定理;正方形的性质;旋转的性质
21世纪教育网(www.21cnjy.com)
4 / 8
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
