2015-2016学年新课标人教A版数学必修一第二章2.1.2指数函数及其性质(共20张PPT)
文档属性
| 名称 | 2015-2016学年新课标人教A版数学必修一第二章2.1.2指数函数及其性质(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 357.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-25 00:00:00 | ||
图片预览






文档简介
课件20张PPT。2.1.2指数函数及其性质 问题一:我是计算机病毒,我的传播速度很快,我
可以由1个分裂成2个,由2个分裂成4个……我分
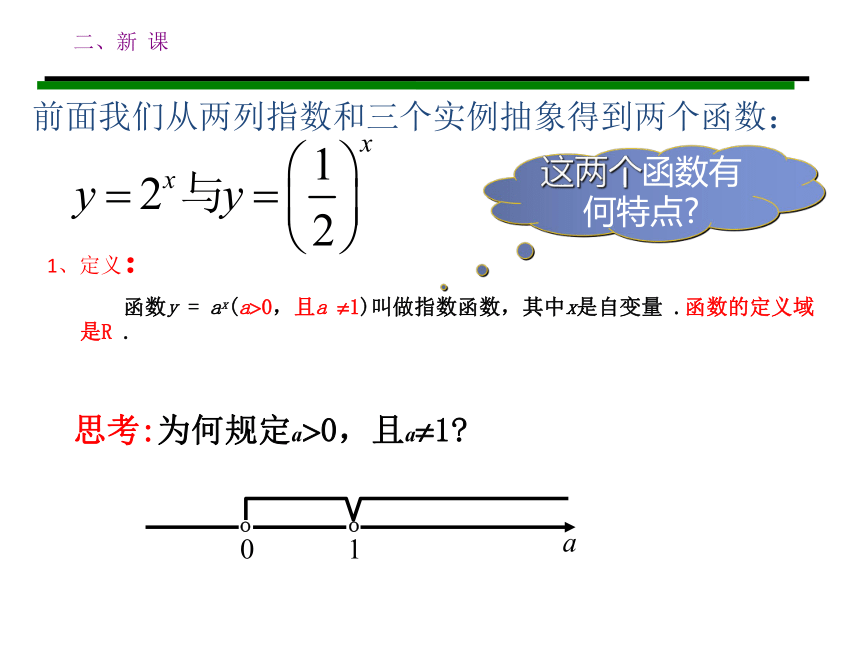
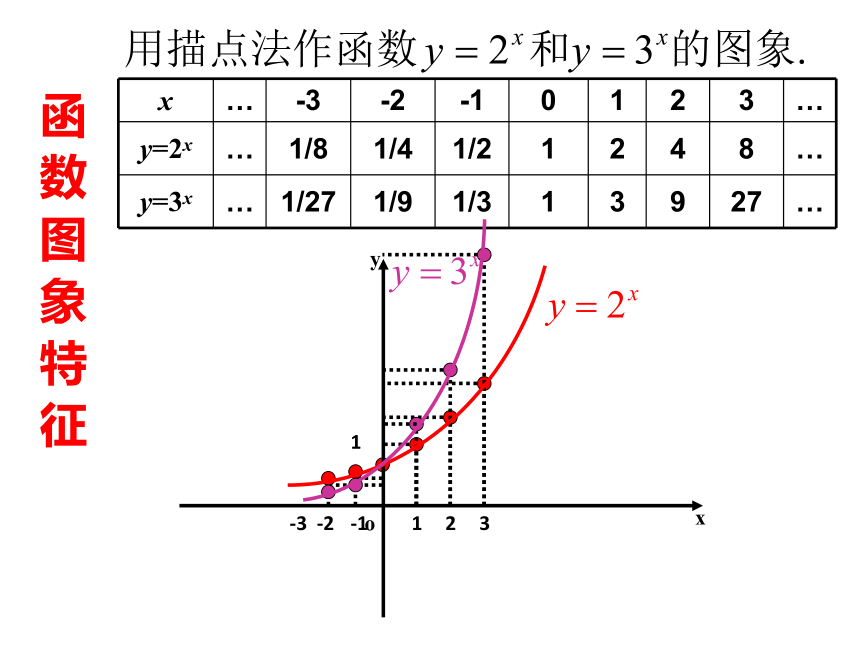
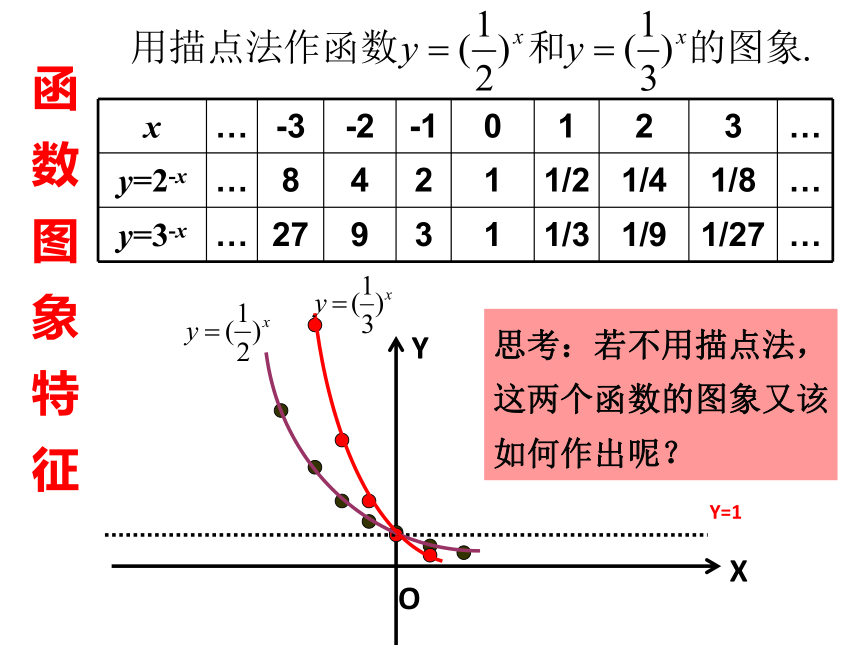
裂x次后得到的个数y与x之间的函数关系式是???一、问题引入引入细胞分裂过程细胞个数第一次第二次第三次2=218=234=22………… 第x次……细胞个数y关于分裂次数x的表达为 问题二、比较下列指数的异同,函数值??什么函数? ①、 ②、能不能把它们看成函数值?一、问题引入一、问题引入问题三、认真观察并回答下列问题: (1)、一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数关系是: (2)、一根1米长的绳子从中间剪一次剩下 米,再从中间剪一次剩下 米,若这条绳子剪x次剩下y米,则y与x的函数关系是:二、新 课 前面我们从两列指数和三个实例抽象得到两个函数: 1、定义:这两个函数有何特点? 函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .函数的定义域是R .思考:为何规定a?0,且a?1? 当a?0时,ax有些会没有意义,如(-2) ,0 等都没有意义;而当a=1时,函数值y恒等于1,没有研究的必要.思考:为何规定a?0,且a?1?二、新 课▲关于指数函数的定义域: 回顾上一节的内容,我们发现指数 中p可以是有理数也可以是无理数,所以指数函数的定义域是R。函 数 图 象 特 征 1函 数 图 象 特 征思考:若不用描点法,
这两个函数的图象又该
如何作出呢?观察右边图象,回答下列问题:问题一:
图象分别在哪几个象限?问题二:
图象的上升、下降与底数a有联系吗?问题三:
图象中有哪些特殊的点?答:四个图象都在第____象限答:当底数__时图象上升;当底数____时图象下降.答:四个图象都经过点____.Ⅰ、Ⅱ底数a由大变小时函数图像在第一象限内按____ 时针方向旋转. 顺2.指数函数的图象和性质1.图象全在x轴上方,与x轴无限接近。1.定义域为R,值域为(0,+?).2.图象过定点(0,1)2.当x=0时,y=13.自左向右图象逐渐上升3.自左向右图象逐渐下降3.在R上是增函数3.在R上是减函数4.图象分布在左下和右上两个区域内4.图象分布在左上和右下两个区域内4.当x>0时,y>1;当x<0时,00时, 01.二、新 课例1、求下列函数的定义域:解、①②③3、例 题:二、新 课例2、比较下列各组数的大小:解:①②、解:③、④、小结比较指数大小的方法:①、构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的),若底数是参变量要注意分类讨论。②、搭桥比较法:用别的数如0或1做桥。数的特征是不同底不同指。二、新 课二、新 课4、练习:(1)、比较大小:(2)、解、①、②、(2)、①、②、(2)、二、新 课③、变式训练:题(2)中,若把 改为a可不可以?若把条件和结论互换可不可以?三、小结1、指数函数概念; 2、指数比较大小的方法; ①、构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的),若底数是参变量要注意分类讨论。②、搭桥比较法:用别的数如0或1做桥。数的特征是不同底不同指。 函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .函数的定义域是R .◆方法指导:利用函数图像研究函数性质是一种直观而形象的方法,记忆指数函数性质时可以联想它的图像;3、指数函数的性质:(1)定义域: 值 域:(2)函数的特殊值:(3)函数的单调性:3.指数函数的图象和性质1.图象全在x轴上方,与x轴无限接近.1.定义域为R,值域为(0,+?).2.图象过定点(0,1)2.当x=0时,y=13.自左向右图象逐渐上升3.自左向右图象逐渐下降3.在R上是增函数3.在R上是减函数4.图象分布在左下和右上两个区域内4.图象分布在左上和右下两个区域内4.当x>0时,y>1;当x<0时,00时, 01.P65,习题2.1 :5、6、7、8。四、作业
可以由1个分裂成2个,由2个分裂成4个……我分
裂x次后得到的个数y与x之间的函数关系式是???一、问题引入引入细胞分裂过程细胞个数第一次第二次第三次2=218=234=22………… 第x次……细胞个数y关于分裂次数x的表达为 问题二、比较下列指数的异同,函数值??什么函数? ①、 ②、能不能把它们看成函数值?一、问题引入一、问题引入问题三、认真观察并回答下列问题: (1)、一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数关系是: (2)、一根1米长的绳子从中间剪一次剩下 米,再从中间剪一次剩下 米,若这条绳子剪x次剩下y米,则y与x的函数关系是:二、新 课 前面我们从两列指数和三个实例抽象得到两个函数: 1、定义:这两个函数有何特点? 函数y = ax(a?0,且a ?1)叫做指数函数,其中x是自变量 .函数的定义域是R .思考:为何规定a?0,且a?1? 当a?0时,ax有些会没有意义,如(-2) ,0 等都没有意义;而当a=1时,函数值y恒等于1,没有研究的必要.思考:为何规定a?0,且a?1?二、新 课▲关于指数函数的定义域: 回顾上一节的内容,我们发现指数 中p可以是有理数也可以是无理数,所以指数函数的定义域是R。函 数 图 象 特 征 1函 数 图 象 特 征思考:若不用描点法,
这两个函数的图象又该
如何作出呢?观察右边图象,回答下列问题:问题一:
图象分别在哪几个象限?问题二:
图象的上升、下降与底数a有联系吗?问题三:
图象中有哪些特殊的点?答:四个图象都在第____象限答:当底数__时图象上升;当底数____时图象下降.答:四个图象都经过点____.Ⅰ、Ⅱ底数a由大变小时函数图像在第一象限内按____ 时针方向旋转. 顺2.指数函数的图象和性质1.图象全在x轴上方,与x轴无限接近。1.定义域为R,值域为(0,+?).2.图象过定点(0,1)2.当x=0时,y=13.自左向右图象逐渐上升3.自左向右图象逐渐下降3.在R上是增函数3.在R上是减函数4.图象分布在左下和右上两个区域内4.图象分布在左上和右下两个区域内4.当x>0时,y>1;当x<0时,0
