人教版八年级下册数学 第十八章 平行四边形 单元测试(含答案)
文档属性
| 名称 | 人教版八年级下册数学 第十八章 平行四边形 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 384.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-30 16:13:58 | ||
图片预览


文档简介
第十八章 平行四边形
一、选择题
1.下列说法错误的是( )
A.一组对边平行且一组对角相等的四边形是平行四边形
B.四条边都相等的四边形是菱形
C.对角线互相垂直的平行四边形是正方形
D.四个角都相等的四边形是矩形
2.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AD∥BC
C.∠ABC=∠ADC,AB=CD D.∠ABD=∠BDC,∠BAD=∠DCB
3.如图,在平行四边形中,点E在线段的延长线上,若,则的度数是( )
A. B. C. D.
4.菱形具有而一般平行四边形不具有的性质是( )
A.对边平行 B.对边相等
C.对角线互相平分 D.对角线平分一组对角
5.如图,矩形中,对角线,相交于点,若,则( )
A.20° B.40° C.80° D.100°
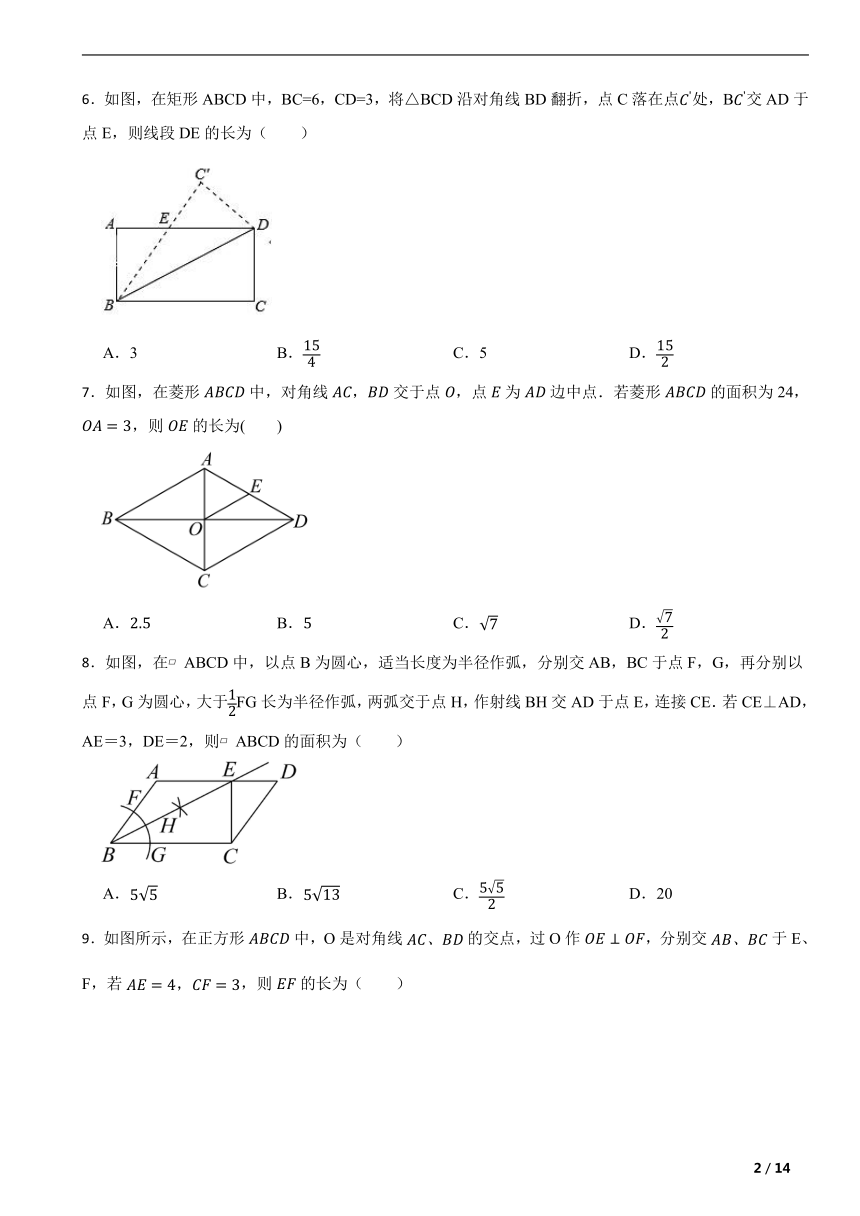
6.如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点处,B交AD于点E,则线段DE的长为( )
A.3 B. C.5 D.
7.如图,在菱形中,对角线,交于点,点为边中点.若菱形的面积为24,,则的长为( )
A. B. C. D.
8.如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB,BC于点F,G,再分别以点F,G为圆心,大于FG长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE.若CE⊥AD,AE=3,DE=2,则 ABCD的面积为( )
A. B. C. D.20
9.如图所示,在正方形中,O是对角线的交点,过O作,分别交于E、F,若,则的长为( )
A.3 B.4 C.5 D.6
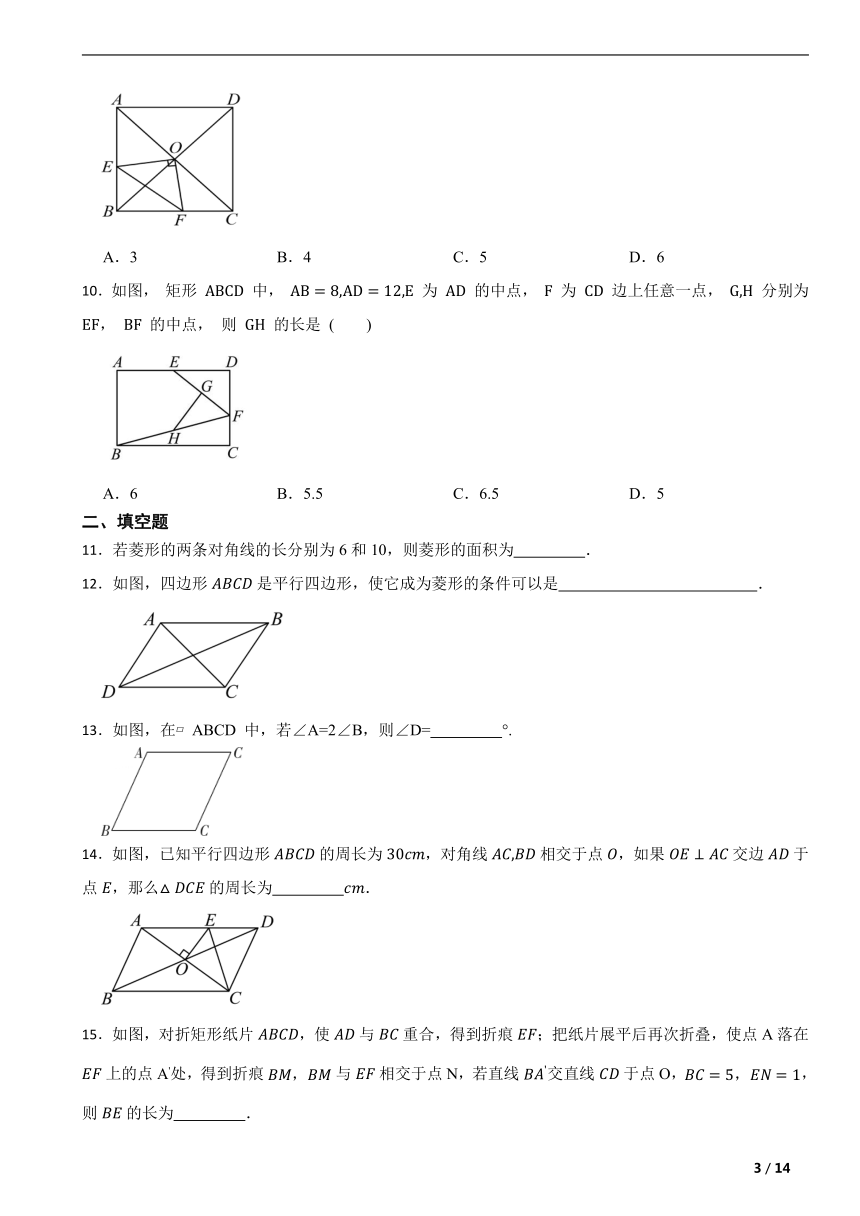
10.如图, 矩形 中, 为 的中点, 为 边上任意一点, 分别为 , 的中点, 则 的长是 ( )
A.6 B.5.5 C.6.5 D.5
二、填空题
11.若菱形的两条对角线的长分别为6和10,则菱形的面积为 .
12.如图,四边形是平行四边形,使它成为菱形的条件可以是 .
13.如图,在 ABCD 中,若∠A=2∠B,则∠D= °.
14.如图,已知平行四边形的周长为,对角线相交于点,如果交边于点,那么的周长为 .
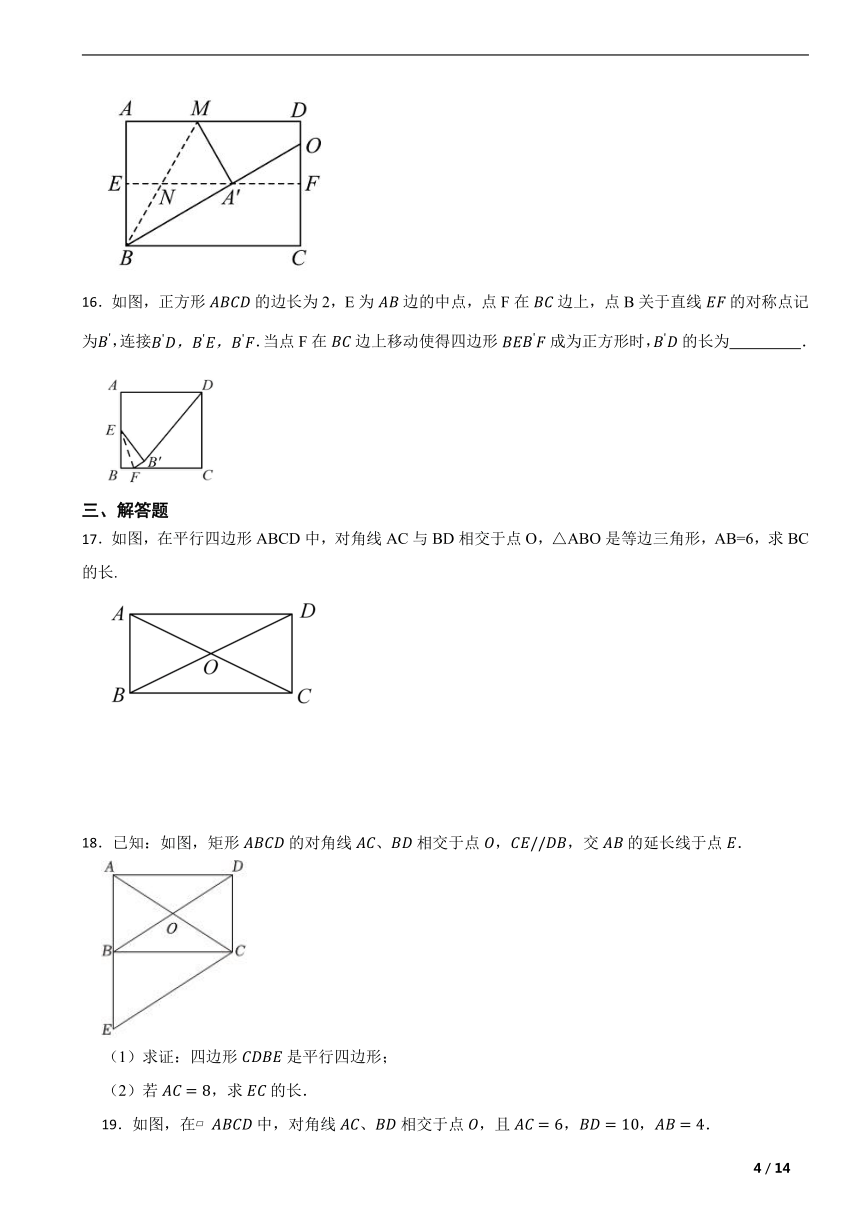
15.如图,对折矩形纸片,使与重合,得到折痕;把纸片展平后再次折叠,使点A落在上的点A'处,得到折痕与相交于点N,若直线交直线于点O,,则的长为 .
16.如图,正方形的边长为2,E为边的中点,点F在边上,点B关于直线的对称点记为,连接.当点F在边上移动使得四边形成为正方形时,的长为 .
三、解答题
17.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=6,求BC的长.
18.已知:如图,矩形的对角线、相交于点,,交的延长线于点.
(1)求证:四边形是平行四边形;
(2)若,求的长.
19.如图,在 中,对角线、相交于点,且,,.
(1)求的度数:
(2)求 的面积.
20.如图,已知四边形是平行四边形,对角线、交于点,是等边三角形.
(1)求证:四边形是矩形;
(2)若,求的长.
21.如图,正方形的边长为,是的中点,是上一点,且.
(1)求证:;
(2)计算的面积.
22.在边长为1的菱形中,以点为圆心,长为半径画弧,交对角线于点.
(1)若时,求的度数:
(2)设,
①当时,求的长;
②用含的代数式表示.
23.如图,在四边形中,,,,,动点P从点A出发,以的速度向点B运动,同时动点Q从点C出发,以的速度向点D运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
(1)当四边形是平行四边形时,求t的值;
(2)当________时,四边形是矩形;若且点Q的移动速度不变,要使四边形能够成为正方形,则P点移动速度是________;
(3)在点P、Q运动过程中,若四边形能够成为菱形,求的长度.
参考答案
1.C
2.C
3.A
4.D
解:A. 对边平行是菱形和一般平行四边形都具有的性质,故不正确;
B. 对边相等是菱形和一般平行四边形都具有的性质,故不正确;
C. 对角线互相平分是菱形和一般平行四边形都具有的性质,故不正确;
D. 对角线平分一组对角是菱形具有而一般平行四边形不具有的性质,故正确;
5.C
6.B
7.A
解:四边形是菱形,,
,,
菱形的面积为,
∴,
,
,
,
为边中点,
,
8.A
9.C
解:四边形是正方形,
,,,
又,
,
,
∴,
,
又,
,
∴中,.
10.D
解:连接,如图所示:
∵四边形是矩形,
,
,E为中点,
,
,
,
∵G,H分别为,中点,
是的中位线,
.
11.30
12.(答案不唯一)
解:根据一组邻边相等的平行四边形是菱形,
∴当时,平行四边形是菱形;
13.60
解:∵ 四边形ABCD是平行四边形,
∴∠A +∠B=180°,∠B=∠D.
又∵∠A=2∠B, ∴3∠B=180°,
∴∠D=∠B=60°.
14.15
15.
16.
17.
18.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
又∵BD∥CE,
四边形DCEB是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴AC=BD,
四边形是平行四边形,
,
,
,
.
19.(1)解:四边形是平行四边形,
,,
,,
,,
,
,
;
(2) 的面积
20.(1)证明:四边形是平行四边形,
,.
是等边三角形,
,
,
四边形是矩形.
(2)解:四边形是矩形,
.
是等边三角形,
,则,
.
21.(1)证明:四边形是正方形,
,,
是的中点,
,
,
即,
,
,
,
即,
,
,
∽,
,
,
,
,
;
(2)解:正方形的边长为,
,,
是的中点,
,
在中,由勾股定理得,
,
,
在中,由勾股定理得,
由知,
的面积.
22.(1)解:∵由题意得:,
∴,
∵四边形是菱形,
∴AD=AB,
∴,
又∵,
∴=∠ABD,
设=,
∵∠AEB是三角形ADE的一个外角,
∴∠AEB=∠ADE+∠DAE=2x,
而在△ABE中,
,
∴,
解得,
∴=.
(2)解:①过点B作于点M,连接交于点O,如图:
∵和是菱形对角线,
∴,且,
∵,,,
,
又∵,BM⊥AE,
,
在Rt△中,由勾股定理得:
,
∵,
∴,
解得:,
在中,由勾股定理得:
,
,
的长为;
②过点B作于点M,连接交于点O,如图:
∵和是菱形对角线,
∴,且,
∵,,
∴,
又∵,
∴,
在直角三角形中,由勾股定理得:
,
∵,
∴,
解得:,
在中,由勾股定理得:
,
在中,由勾股定理得:
,
∴,
.
23.(1)解:根据题意,得AP=t,CQ=3t,则BP=18-t,
∵四边形是平行四边形,
∴BP=CQ,即18-t=3t,
解得:t=4.5,
∴当四边形是平行四边形时,t的值为4.5;
(2)7,4
(3)解:解:如图,
由(1)(2)得AP=t,BP=18-t,DQ=28-3t,
∵四边形是菱形,
∴,
∴,
解得:,
∴,,
∵,,
∴,
在中,,
∴ 若四边形能够成为菱形, 则AD的长为12cm.
1 / 1
一、选择题
1.下列说法错误的是( )
A.一组对边平行且一组对角相等的四边形是平行四边形
B.四条边都相等的四边形是菱形
C.对角线互相垂直的平行四边形是正方形
D.四个角都相等的四边形是矩形
2.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AD∥BC
C.∠ABC=∠ADC,AB=CD D.∠ABD=∠BDC,∠BAD=∠DCB
3.如图,在平行四边形中,点E在线段的延长线上,若,则的度数是( )
A. B. C. D.
4.菱形具有而一般平行四边形不具有的性质是( )
A.对边平行 B.对边相等
C.对角线互相平分 D.对角线平分一组对角
5.如图,矩形中,对角线,相交于点,若,则( )
A.20° B.40° C.80° D.100°
6.如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点处,B交AD于点E,则线段DE的长为( )
A.3 B. C.5 D.
7.如图,在菱形中,对角线,交于点,点为边中点.若菱形的面积为24,,则的长为( )
A. B. C. D.
8.如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB,BC于点F,G,再分别以点F,G为圆心,大于FG长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE.若CE⊥AD,AE=3,DE=2,则 ABCD的面积为( )
A. B. C. D.20
9.如图所示,在正方形中,O是对角线的交点,过O作,分别交于E、F,若,则的长为( )
A.3 B.4 C.5 D.6
10.如图, 矩形 中, 为 的中点, 为 边上任意一点, 分别为 , 的中点, 则 的长是 ( )
A.6 B.5.5 C.6.5 D.5
二、填空题
11.若菱形的两条对角线的长分别为6和10,则菱形的面积为 .
12.如图,四边形是平行四边形,使它成为菱形的条件可以是 .
13.如图,在 ABCD 中,若∠A=2∠B,则∠D= °.
14.如图,已知平行四边形的周长为,对角线相交于点,如果交边于点,那么的周长为 .
15.如图,对折矩形纸片,使与重合,得到折痕;把纸片展平后再次折叠,使点A落在上的点A'处,得到折痕与相交于点N,若直线交直线于点O,,则的长为 .
16.如图,正方形的边长为2,E为边的中点,点F在边上,点B关于直线的对称点记为,连接.当点F在边上移动使得四边形成为正方形时,的长为 .
三、解答题
17.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=6,求BC的长.
18.已知:如图,矩形的对角线、相交于点,,交的延长线于点.
(1)求证:四边形是平行四边形;
(2)若,求的长.
19.如图,在 中,对角线、相交于点,且,,.
(1)求的度数:
(2)求 的面积.
20.如图,已知四边形是平行四边形,对角线、交于点,是等边三角形.
(1)求证:四边形是矩形;
(2)若,求的长.
21.如图,正方形的边长为,是的中点,是上一点,且.
(1)求证:;
(2)计算的面积.
22.在边长为1的菱形中,以点为圆心,长为半径画弧,交对角线于点.
(1)若时,求的度数:
(2)设,
①当时,求的长;
②用含的代数式表示.
23.如图,在四边形中,,,,,动点P从点A出发,以的速度向点B运动,同时动点Q从点C出发,以的速度向点D运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.
(1)当四边形是平行四边形时,求t的值;
(2)当________时,四边形是矩形;若且点Q的移动速度不变,要使四边形能够成为正方形,则P点移动速度是________;
(3)在点P、Q运动过程中,若四边形能够成为菱形,求的长度.
参考答案
1.C
2.C
3.A
4.D
解:A. 对边平行是菱形和一般平行四边形都具有的性质,故不正确;
B. 对边相等是菱形和一般平行四边形都具有的性质,故不正确;
C. 对角线互相平分是菱形和一般平行四边形都具有的性质,故不正确;
D. 对角线平分一组对角是菱形具有而一般平行四边形不具有的性质,故正确;
5.C
6.B
7.A
解:四边形是菱形,,
,,
菱形的面积为,
∴,
,
,
,
为边中点,
,
8.A
9.C
解:四边形是正方形,
,,,
又,
,
,
∴,
,
又,
,
∴中,.
10.D
解:连接,如图所示:
∵四边形是矩形,
,
,E为中点,
,
,
,
∵G,H分别为,中点,
是的中位线,
.
11.30
12.(答案不唯一)
解:根据一组邻边相等的平行四边形是菱形,
∴当时,平行四边形是菱形;
13.60
解:∵ 四边形ABCD是平行四边形,
∴∠A +∠B=180°,∠B=∠D.
又∵∠A=2∠B, ∴3∠B=180°,
∴∠D=∠B=60°.
14.15
15.
16.
17.
18.(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
又∵BD∥CE,
四边形DCEB是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴AC=BD,
四边形是平行四边形,
,
,
,
.
19.(1)解:四边形是平行四边形,
,,
,,
,,
,
,
;
(2) 的面积
20.(1)证明:四边形是平行四边形,
,.
是等边三角形,
,
,
四边形是矩形.
(2)解:四边形是矩形,
.
是等边三角形,
,则,
.
21.(1)证明:四边形是正方形,
,,
是的中点,
,
,
即,
,
,
,
即,
,
,
∽,
,
,
,
,
;
(2)解:正方形的边长为,
,,
是的中点,
,
在中,由勾股定理得,
,
,
在中,由勾股定理得,
由知,
的面积.
22.(1)解:∵由题意得:,
∴,
∵四边形是菱形,
∴AD=AB,
∴,
又∵,
∴=∠ABD,
设=,
∵∠AEB是三角形ADE的一个外角,
∴∠AEB=∠ADE+∠DAE=2x,
而在△ABE中,
,
∴,
解得,
∴=.
(2)解:①过点B作于点M,连接交于点O,如图:
∵和是菱形对角线,
∴,且,
∵,,,
,
又∵,BM⊥AE,
,
在Rt△中,由勾股定理得:
,
∵,
∴,
解得:,
在中,由勾股定理得:
,
,
的长为;
②过点B作于点M,连接交于点O,如图:
∵和是菱形对角线,
∴,且,
∵,,
∴,
又∵,
∴,
在直角三角形中,由勾股定理得:
,
∵,
∴,
解得:,
在中,由勾股定理得:
,
在中,由勾股定理得:
,
∴,
.
23.(1)解:根据题意,得AP=t,CQ=3t,则BP=18-t,
∵四边形是平行四边形,
∴BP=CQ,即18-t=3t,
解得:t=4.5,
∴当四边形是平行四边形时,t的值为4.5;
(2)7,4
(3)解:解:如图,
由(1)(2)得AP=t,BP=18-t,DQ=28-3t,
∵四边形是菱形,
∴,
∴,
解得:,
∴,,
∵,,
∴,
在中,,
∴ 若四边形能够成为菱形, 则AD的长为12cm.
1 / 1
