苏科版数学八年级下册期中试题【培优】(含答案)
文档属性
| 名称 | 苏科版数学八年级下册期中试题【培优】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 08:39:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏科版数学八年级下册期中试题【培优】
一、单选题
1.(2024九上·武汉月考)的纸是中国优秀的传统文化.如图的纸图案中,是中心对称图形的是( )
A. B.
C. D.
2.(2023九上·平泉期末)某数学兴趣小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的统计图,那么符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副只有四种花色的52张普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.抛掷一个质地均匀的正六面体骰子,向上的面点数是4
D.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
3.(2024八上·长春高新技术产业开发开学考)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.(2024八上·三亚期末)如图,将矩形沿对角线折叠,使点和点重合,若,则的长为( )
A. B. C. D.
5.(2024八下·麒麟月考)如图,在中,若,则的度数为( )
A. B. C. D.
6.(2023九上·大连月考)下列图形中,是中心对称图形的是( )
A. B.
C. D.
7.(2022八上·柯桥月考)直线上有三个正方形、、,若、的面积分别为3和8,则的面积为 ( ).
A.11 B.24 C.5 D.无法确定
8.(2024八下·秦都月考)下列条件中不能使四边形是平行四边形的是( )
A. B.
C. D.
9.(2024九下·河西模拟)如图,,平分,交于C,以点B为圆心,以任意长为半径作弧,分别交于M,N两点,再分别以M,N两点为圆心,都以一个大于的长度为半径作弧,两弧相交于点P,射线与相交于点D.若,,则的长为( )
A.3 B.4 C.5 D.6
10.(2024九上·浙江期中)如图,矩形ABCD被分割成4个直角三角形和1个小矩形后仍是中心对称图形.设上下两个直角三角形的面积都为S1,左右两个直角三角形的面积都为S2,中间小矩形的面积为S3,若对角线EF∥BC,则矩形ABCD的面积一定可以表示为( )
A.4S1 B.8S2 C.8S3 D.2S1+4S3
二、填空题
11.(2024八下·松原期末)如图,为了检查平行四边形书架 ABCD 的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线 AC,BD 的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理 .
12.(2023九上·大厂期中)下图是双11期间某购物平台的抽奖图,那么该图的中奖概率为 .
13.(2020八下·拱墅期末)如图,在△ABC中,∠ACB=90°,点D在边AB上(不与点A,B重合),DE⊥AC于点E,DF⊥BC于点F,连接EF。若AC=3,BC=2,则EF的最小值为 。
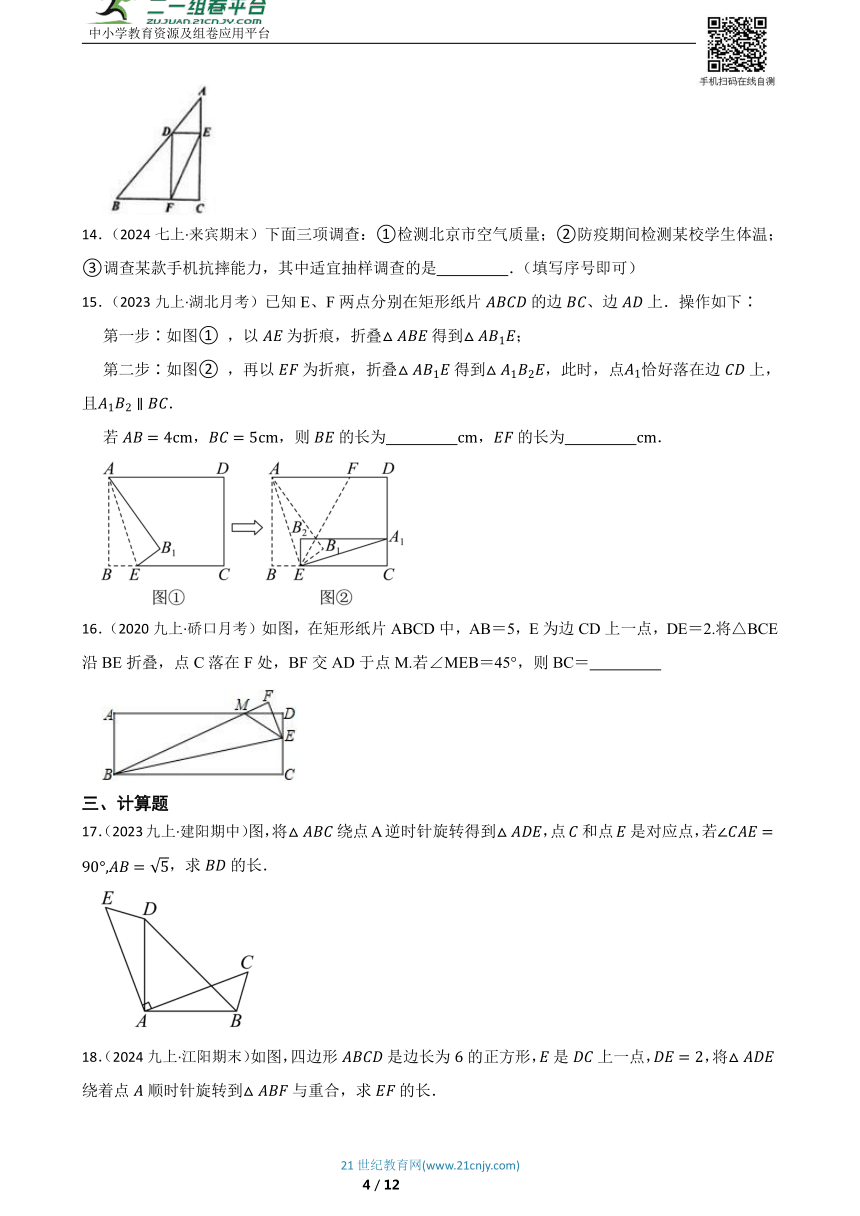
14.(2024七上·来宾期末)下面三项调查:①检测北京市空气质量;②防疫期间检测某校学生体温;③调查某款手机抗摔能力,其中适宜抽样调查的是 .(填写序号即可)
15.(2023九上·湖北月考)已知E、F两点分别在矩形纸片的边、边上.操作如下∶
第一步∶如图① ,以为折痕,折叠得到;
第二步∶如图② ,再以为折痕,折叠得到,此时,点恰好落在边上,且.
若,,则的长为 ,的长为 .
16.(2020九上·硚口月考)如图,在矩形纸片ABCD中,AB=5,E为边CD上一点,DE=2.将△BCE沿BE折叠,点C落在F处,BF交AD于点M.若∠MEB=45°,则BC=
三、计算题
17.(2023九上·建阳期中)图,将绕点A逆时针旋转得到,点和点是对应点,若,求的长.
18.(2024九上·江阳期末)如图,四边形是边长为的正方形,是上一点,,将绕着点顺时针旋转到与重合,求的长.
19.(2024八下·新吴期末)如图,在矩形中,对角线,相交于点,,,点在线段上,从点至点运动,连接,以为边作等边,点和点分别位于两侧.
(1)当点运动到点时,求的长;
(2)点在线段上从点至点运动过程中,求的最小值.
四、解答题
20.现在都采用政府统一采购行为,教育局对各个学校的校服征订的办法,在教育局的样品室里摆放着12个样品,有12种不同的价位,分别为50,60,70,80,90,100,110,120,130,140,150,160元,现要对某校1500名学生统一征订校服,由于价格相差甚远,于是学校决定征求家长的意见,想要制作一张调查表,对家长的意见进行调查,请问,你该怎样设计这张调查表.(要求家长用打“√”的形式来表达).
21.(2024八下·苏州工业园月考)如图,中,,,,将绕点按顺时针旋转,得到,求的长度.
22.(2023八下·秦淮期末)为了响应国家提出的“每天锻炼1小时”的号召,某校积极开展了形式多样的“阳光体育”运动,小红对该班同学参加锻炼的情况进行了统计,(每人只能选其中一项)并绘制了下面的两幅统计图,请根据图中提供的信息解答下列问题:
(1)小红这次一共调查了多少名学生?
(2)通过计算补全条形统计图.
(3)若该校有2000名学生,请估计该校喜欢乒乓球的学生约有多少人?
23.(2024八下·六安期中) 如图,将,的长方形,沿过顶点A的直线为折痕折叠,使顶点B落在边上的点Q处.
(1)求的长;
(2)求的长.
24.(2023·巧家模拟)如图,菱形的对角线与交于点,于点,交于点,于点.
(1)判断四边形的形状,并写出证明过程.
(2)若,,求的长,
25.(2023九上·龙湾开学考)如图,在中,于点,,分别是,的中点,是的中点,的延长线交线段于点,连接,,.
(1)求证:四边形是平行四边形;
(2)若,,,求的长.
答案解析部分
1.【答案】C
【知识点】中心对称及中心对称图形
2.【答案】C
【知识点】利用频率估计概率
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】B
【知识点】矩形的性质
5.【答案】B
【知识点】平行四边形的性质
6.【答案】B
【知识点】中心对称及中心对称图形
7.【答案】A
【知识点】勾股定理;正方形的性质
8.【答案】C
【知识点】平行四边形的判定
9.【答案】C
【知识点】等腰三角形的性质;勾股定理;菱形的判定与性质;尺规作图-作角的平分线
10.【答案】A
【知识点】矩形的性质;中心对称及中心对称图形
11.【答案】对角线相等的平行四边形是矩形,矩形的四个角都是直角.
【知识点】矩形的判定
12.【答案】
【知识点】概率公式
13.【答案】
【知识点】垂线段最短及其应用;三角形的面积;矩形的性质
14.【答案】①③
【知识点】全面调查与抽样调查
15.【答案】;
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
16.【答案】15
【知识点】三角形全等的判定;勾股定理;矩形的性质;翻折变换(折叠问题)
17.【答案】
【知识点】勾股定理;旋转的性质
18.【答案】
【知识点】勾股定理;正方形的性质;旋转的性质
19.【答案】(1)2
(2)
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质;三角形全等的判定-SAS
20.【答案】解:如表格所示:
价格范围 在你认为合理的价格后面打“√”,只能选一个
50~60
70~80
90~100
110~120
130~140
150~160
【知识点】收集数据的过程与方法
21.【答案】4
【知识点】等边三角形的判定与性质;勾股定理;旋转的性质
22.【答案】(1)解:由统计图可知,(名)
答:这次一共调查50名学生.
(2)解:可求出打乒乓球的人数为:(名),
补全统计图如下图所示,
(3)解:喜欢乒乓球的学生所占比例为:
∴该校喜欢乒乓球的学生有,
答:估计该校喜欢乒乓球的学生约200人.
【知识点】扇形统计图;条形统计图
23.【答案】(1)解:由折叠的性质可知,
∴,
∵四边形是矩形,
∴,
∵,
∴,
∴线段的长度是;
(2)解:由(1)可知,
∴,
设,则,
∴,
∴,
解得:,
∴线段的长度是,
∴线段的长度是.
【知识点】三角形全等及其性质;勾股定理;矩形的性质;翻折变换(折叠问题)
24.【答案】(1)解:四边形是矩形.
证明:∵,,
∴.
∵四边形是菱形,∴,
∴,
∴,
∴四边形是矩形.
(2)解:如图,连接.
∵四边形是菱形,
∴垂直平分,
∴.
由(1)知,四边形是矩形,
∴.
设,则,
在中,由勾股定理,得,解得,
∴.
【知识点】勾股定理;菱形的性质;矩形的判定
25.【答案】(1)证明:,分别是,的中点,
是的中位线,
,
,
是的中点,
,
在和中,
,
≌,
,
四边形是平行四边形.
(2)解:
,
,,
,
是的中点,
,
,
是菱形,
,
.
【知识点】三角形全等的判定;勾股定理的应用;平行四边形的判定与性质;菱形的判定与性质;三角形的中位线定理
21世纪教育网(www.21cnjy.com)
12 / 12
苏科版数学八年级下册期中试题【培优】
一、单选题
1.(2024九上·武汉月考)的纸是中国优秀的传统文化.如图的纸图案中,是中心对称图形的是( )
A. B.
C. D.
2.(2023九上·平泉期末)某数学兴趣小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图所示的统计图,那么符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副只有四种花色的52张普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.抛掷一个质地均匀的正六面体骰子,向上的面点数是4
D.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
3.(2024八上·长春高新技术产业开发开学考)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.(2024八上·三亚期末)如图,将矩形沿对角线折叠,使点和点重合,若,则的长为( )
A. B. C. D.
5.(2024八下·麒麟月考)如图,在中,若,则的度数为( )
A. B. C. D.
6.(2023九上·大连月考)下列图形中,是中心对称图形的是( )
A. B.
C. D.
7.(2022八上·柯桥月考)直线上有三个正方形、、,若、的面积分别为3和8,则的面积为 ( ).
A.11 B.24 C.5 D.无法确定
8.(2024八下·秦都月考)下列条件中不能使四边形是平行四边形的是( )
A. B.
C. D.
9.(2024九下·河西模拟)如图,,平分,交于C,以点B为圆心,以任意长为半径作弧,分别交于M,N两点,再分别以M,N两点为圆心,都以一个大于的长度为半径作弧,两弧相交于点P,射线与相交于点D.若,,则的长为( )
A.3 B.4 C.5 D.6
10.(2024九上·浙江期中)如图,矩形ABCD被分割成4个直角三角形和1个小矩形后仍是中心对称图形.设上下两个直角三角形的面积都为S1,左右两个直角三角形的面积都为S2,中间小矩形的面积为S3,若对角线EF∥BC,则矩形ABCD的面积一定可以表示为( )
A.4S1 B.8S2 C.8S3 D.2S1+4S3
二、填空题
11.(2024八下·松原期末)如图,为了检查平行四边形书架 ABCD 的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线 AC,BD 的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理 .
12.(2023九上·大厂期中)下图是双11期间某购物平台的抽奖图,那么该图的中奖概率为 .
13.(2020八下·拱墅期末)如图,在△ABC中,∠ACB=90°,点D在边AB上(不与点A,B重合),DE⊥AC于点E,DF⊥BC于点F,连接EF。若AC=3,BC=2,则EF的最小值为 。
14.(2024七上·来宾期末)下面三项调查:①检测北京市空气质量;②防疫期间检测某校学生体温;③调查某款手机抗摔能力,其中适宜抽样调查的是 .(填写序号即可)
15.(2023九上·湖北月考)已知E、F两点分别在矩形纸片的边、边上.操作如下∶
第一步∶如图① ,以为折痕,折叠得到;
第二步∶如图② ,再以为折痕,折叠得到,此时,点恰好落在边上,且.
若,,则的长为 ,的长为 .
16.(2020九上·硚口月考)如图,在矩形纸片ABCD中,AB=5,E为边CD上一点,DE=2.将△BCE沿BE折叠,点C落在F处,BF交AD于点M.若∠MEB=45°,则BC=
三、计算题
17.(2023九上·建阳期中)图,将绕点A逆时针旋转得到,点和点是对应点,若,求的长.
18.(2024九上·江阳期末)如图,四边形是边长为的正方形,是上一点,,将绕着点顺时针旋转到与重合,求的长.
19.(2024八下·新吴期末)如图,在矩形中,对角线,相交于点,,,点在线段上,从点至点运动,连接,以为边作等边,点和点分别位于两侧.
(1)当点运动到点时,求的长;
(2)点在线段上从点至点运动过程中,求的最小值.
四、解答题
20.现在都采用政府统一采购行为,教育局对各个学校的校服征订的办法,在教育局的样品室里摆放着12个样品,有12种不同的价位,分别为50,60,70,80,90,100,110,120,130,140,150,160元,现要对某校1500名学生统一征订校服,由于价格相差甚远,于是学校决定征求家长的意见,想要制作一张调查表,对家长的意见进行调查,请问,你该怎样设计这张调查表.(要求家长用打“√”的形式来表达).
21.(2024八下·苏州工业园月考)如图,中,,,,将绕点按顺时针旋转,得到,求的长度.
22.(2023八下·秦淮期末)为了响应国家提出的“每天锻炼1小时”的号召,某校积极开展了形式多样的“阳光体育”运动,小红对该班同学参加锻炼的情况进行了统计,(每人只能选其中一项)并绘制了下面的两幅统计图,请根据图中提供的信息解答下列问题:
(1)小红这次一共调查了多少名学生?
(2)通过计算补全条形统计图.
(3)若该校有2000名学生,请估计该校喜欢乒乓球的学生约有多少人?
23.(2024八下·六安期中) 如图,将,的长方形,沿过顶点A的直线为折痕折叠,使顶点B落在边上的点Q处.
(1)求的长;
(2)求的长.
24.(2023·巧家模拟)如图,菱形的对角线与交于点,于点,交于点,于点.
(1)判断四边形的形状,并写出证明过程.
(2)若,,求的长,
25.(2023九上·龙湾开学考)如图,在中,于点,,分别是,的中点,是的中点,的延长线交线段于点,连接,,.
(1)求证:四边形是平行四边形;
(2)若,,,求的长.
答案解析部分
1.【答案】C
【知识点】中心对称及中心对称图形
2.【答案】C
【知识点】利用频率估计概率
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】B
【知识点】矩形的性质
5.【答案】B
【知识点】平行四边形的性质
6.【答案】B
【知识点】中心对称及中心对称图形
7.【答案】A
【知识点】勾股定理;正方形的性质
8.【答案】C
【知识点】平行四边形的判定
9.【答案】C
【知识点】等腰三角形的性质;勾股定理;菱形的判定与性质;尺规作图-作角的平分线
10.【答案】A
【知识点】矩形的性质;中心对称及中心对称图形
11.【答案】对角线相等的平行四边形是矩形,矩形的四个角都是直角.
【知识点】矩形的判定
12.【答案】
【知识点】概率公式
13.【答案】
【知识点】垂线段最短及其应用;三角形的面积;矩形的性质
14.【答案】①③
【知识点】全面调查与抽样调查
15.【答案】;
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题)
16.【答案】15
【知识点】三角形全等的判定;勾股定理;矩形的性质;翻折变换(折叠问题)
17.【答案】
【知识点】勾股定理;旋转的性质
18.【答案】
【知识点】勾股定理;正方形的性质;旋转的性质
19.【答案】(1)2
(2)
【知识点】等边三角形的判定与性质;勾股定理;矩形的性质;三角形全等的判定-SAS
20.【答案】解:如表格所示:
价格范围 在你认为合理的价格后面打“√”,只能选一个
50~60
70~80
90~100
110~120
130~140
150~160
【知识点】收集数据的过程与方法
21.【答案】4
【知识点】等边三角形的判定与性质;勾股定理;旋转的性质
22.【答案】(1)解:由统计图可知,(名)
答:这次一共调查50名学生.
(2)解:可求出打乒乓球的人数为:(名),
补全统计图如下图所示,
(3)解:喜欢乒乓球的学生所占比例为:
∴该校喜欢乒乓球的学生有,
答:估计该校喜欢乒乓球的学生约200人.
【知识点】扇形统计图;条形统计图
23.【答案】(1)解:由折叠的性质可知,
∴,
∵四边形是矩形,
∴,
∵,
∴,
∴线段的长度是;
(2)解:由(1)可知,
∴,
设,则,
∴,
∴,
解得:,
∴线段的长度是,
∴线段的长度是.
【知识点】三角形全等及其性质;勾股定理;矩形的性质;翻折变换(折叠问题)
24.【答案】(1)解:四边形是矩形.
证明:∵,,
∴.
∵四边形是菱形,∴,
∴,
∴,
∴四边形是矩形.
(2)解:如图,连接.
∵四边形是菱形,
∴垂直平分,
∴.
由(1)知,四边形是矩形,
∴.
设,则,
在中,由勾股定理,得,解得,
∴.
【知识点】勾股定理;菱形的性质;矩形的判定
25.【答案】(1)证明:,分别是,的中点,
是的中位线,
,
,
是的中点,
,
在和中,
,
≌,
,
四边形是平行四边形.
(2)解:
,
,,
,
是的中点,
,
,
是菱形,
,
.
【知识点】三角形全等的判定;勾股定理的应用;平行四边形的判定与性质;菱形的判定与性质;三角形的中位线定理
21世纪教育网(www.21cnjy.com)
12 / 12
同课章节目录
