1.1直角三角形的性质与判定(I) 同步练习(含答案)
文档属性
| 名称 | 1.1直角三角形的性质与判定(I) 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 323.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.1直角三角形的性质与判定(I)
一、填空题
1.如果一个直角三角形的两边分别是6,8,那么斜边上的中线是 .
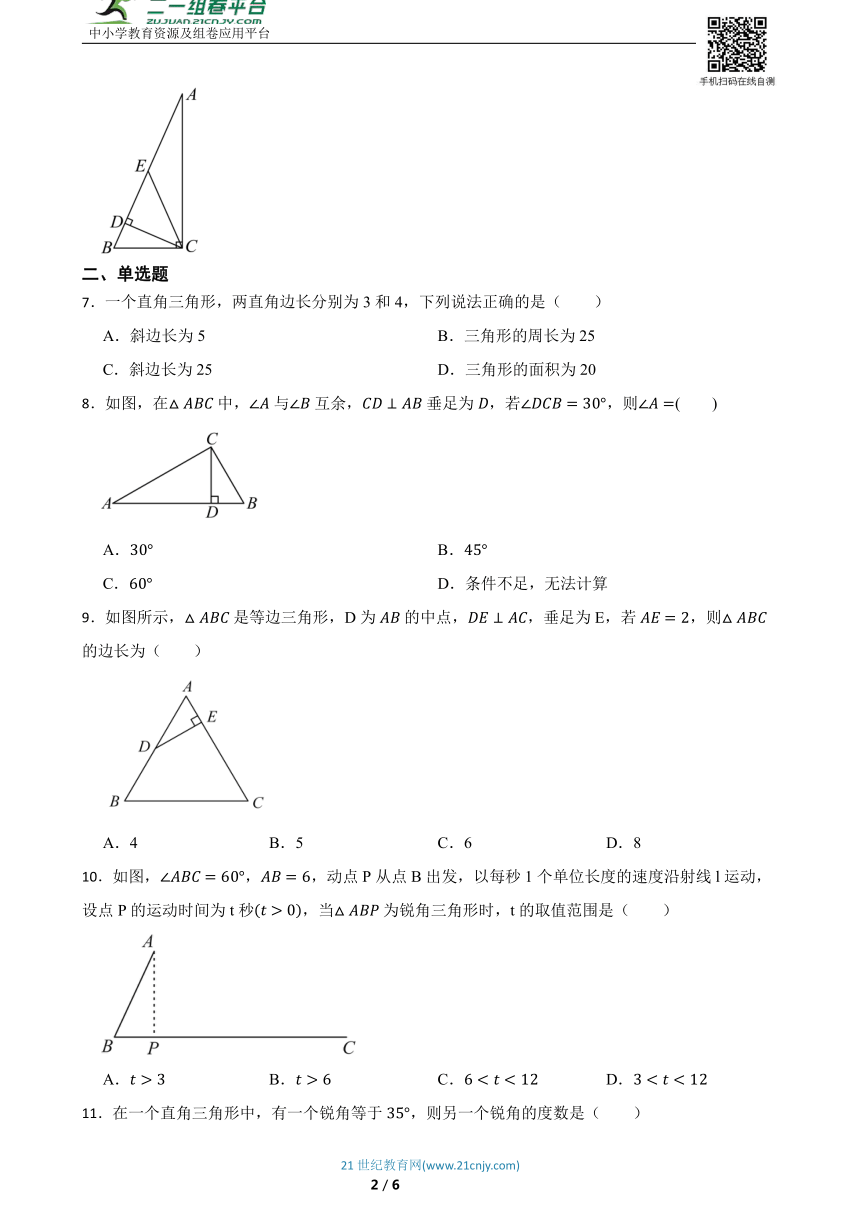
2.如图,在中,,点D在上,于点交与点F.若,则 .
3.在三角形中,,垂足为D,则有,其理由是 .
4.在中,,,,则 .
5.如图,在中,,,,分别以点,点为圆心,大于的长为半径画弧,两弧相交于点,,作直线交于点,连接,则的长是 .
6.如图,在中,,于点D,,E是斜边的中点,连接,则的度数为 .
二、单选题
7.一个直角三角形,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为5 B.三角形的周长为25
C.斜边长为25 D.三角形的面积为20
8.如图,在中,与互余,垂足为,若,则( )
A. B.
C. D.条件不足,无法计算
9.如图所示,是等边三角形,D为的中点,,垂足为E,若,则的边长为( )
A.4 B.5 C.6 D.8
10.如图,,,动点P从点B出发,以每秒1个单位长度的速度沿射线l运动,设点P的运动时间为t秒,当为锐角三角形时,t的取值范围是( )
A. B. C. D.
11.在一个直角三角形中,有一个锐角等于,则另一个锐角的度数是( )
A. B. C. D.
三、解答题
12.AD是等腰△ABC中BC边上的高,且AD=BC,请通过画图求出∠ABC所有可能的值.
四、计算题
13.如图,在中,于F,于E,M为的中点.
(1)若,,求的周长;
(2)若是等边三角形,求的度数.
14.若点是射线上异于起点的一点,且,则称点为射线的倍衍生点.例如,在图1中,点在射线上,且,则点为射线的2倍衍生点;点在射线上,且,则点为射线的倍衍生点.
(1)填空:已知,
①若点为射线的3倍衍生点,则 ;
②若点为射线的倍衍生点,则 ;
(2)如图2,已知是等边三角形,点为射线的倍衍生点.
①若点为射线的1倍衍生点,满足,求的值;
②若点是直线上异于点的一点,满足,请直接用含的式子表示.
五、作图题
15.如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图
(1)在图1中作直角,使点在格点上;
(2)在图2中的线段上作点,使最短.
六、综合题
16.如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.
17.在 Rt 中, , 斜边 , 则斜边上的中线 .
18.如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东方向,船以25海里时的速度继续航行4小时后到达C点,此时钓鱼岛A在船的北偏东方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
答案解析部分
1.【答案】4或5
【知识点】直角三角形斜边上的中线
2.【答案】
【知识点】直角三角形的性质
3.【答案】同角的余角相等
【知识点】余角、补角及其性质;直角三角形的性质
4.【答案】6
【知识点】含30°角的直角三角形;直角三角形的性质
5.【答案】
【知识点】尺规作图-垂直平分线;直角三角形斜边上的中线
6.【答案】45
【知识点】余角、补角及其性质;等腰三角形的性质;直角三角形斜边上的中线
7.【答案】A
【知识点】直角三角形的性质
8.【答案】A
【知识点】余角、补角及其性质;直角三角形的性质
9.【答案】D
【知识点】等边三角形的性质;含30°角的直角三角形
10.【答案】D
【知识点】含30°角的直角三角形
11.【答案】D
【知识点】直角三角形的性质
12.【答案】∠ABC所有可能的值为:45°或30°150°
【知识点】含30°角的直角三角形
13.【答案】(1)的周长为14;
(2).
【知识点】三角形内角和定理;等腰三角形的判定与性质;直角三角形斜边上的中线
14.【答案】(1)①12;②2或4
(2)①;②为或或.
【知识点】等腰三角形的判定与性质;等边三角形的性质;含30°角的直角三角形
15.【答案】(1)解:如图1,即为所求;
(2)解:如图2,点Q即为所求;
【知识点】垂线段最短及其应用;直角三角形的性质
16.【答案】(1)解:∵AD⊥BC,
∴在Rt△BAD中,∠BAD+∠B=90°,
又∵∠B=64°,∴∠BAD=26°;
∴在Rt△BAD中,∠DAC+∠C=90°,
又∵∠C=56°,∴∠DAC=34°;
(2)解:∵AD⊥BC,DE平分∠ADB,∴∠BDE=45°,
在△BED中,∠B=64°,∴∠B+∠BDE=109°,
∵∠AED=∠B+∠BDE,
∴∠AED=109°.
【知识点】三角形的外角性质;直角三角形的性质
17.【答案】4
【知识点】直角三角形斜边上的中线
18.【答案】船继续航行50海里与钓鱼岛A的距离最近
【知识点】三角形的外角性质;等腰三角形的判定;含30°角的直角三角形
21世纪教育网(www.21cnjy.com)
1 / 6
1.1直角三角形的性质与判定(I)
一、填空题
1.如果一个直角三角形的两边分别是6,8,那么斜边上的中线是 .
2.如图,在中,,点D在上,于点交与点F.若,则 .
3.在三角形中,,垂足为D,则有,其理由是 .
4.在中,,,,则 .
5.如图,在中,,,,分别以点,点为圆心,大于的长为半径画弧,两弧相交于点,,作直线交于点,连接,则的长是 .
6.如图,在中,,于点D,,E是斜边的中点,连接,则的度数为 .
二、单选题
7.一个直角三角形,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为5 B.三角形的周长为25
C.斜边长为25 D.三角形的面积为20
8.如图,在中,与互余,垂足为,若,则( )
A. B.
C. D.条件不足,无法计算
9.如图所示,是等边三角形,D为的中点,,垂足为E,若,则的边长为( )
A.4 B.5 C.6 D.8
10.如图,,,动点P从点B出发,以每秒1个单位长度的速度沿射线l运动,设点P的运动时间为t秒,当为锐角三角形时,t的取值范围是( )
A. B. C. D.
11.在一个直角三角形中,有一个锐角等于,则另一个锐角的度数是( )
A. B. C. D.
三、解答题
12.AD是等腰△ABC中BC边上的高,且AD=BC,请通过画图求出∠ABC所有可能的值.
四、计算题
13.如图,在中,于F,于E,M为的中点.
(1)若,,求的周长;
(2)若是等边三角形,求的度数.
14.若点是射线上异于起点的一点,且,则称点为射线的倍衍生点.例如,在图1中,点在射线上,且,则点为射线的2倍衍生点;点在射线上,且,则点为射线的倍衍生点.
(1)填空:已知,
①若点为射线的3倍衍生点,则 ;
②若点为射线的倍衍生点,则 ;
(2)如图2,已知是等边三角形,点为射线的倍衍生点.
①若点为射线的1倍衍生点,满足,求的值;
②若点是直线上异于点的一点,满足,请直接用含的式子表示.
五、作图题
15.如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图
(1)在图1中作直角,使点在格点上;
(2)在图2中的线段上作点,使最短.
六、综合题
16.如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.
17.在 Rt 中, , 斜边 , 则斜边上的中线 .
18.如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东方向,船以25海里时的速度继续航行4小时后到达C点,此时钓鱼岛A在船的北偏东方向.请问船继续航行多少海里与钓鱼岛A的距离最近?
答案解析部分
1.【答案】4或5
【知识点】直角三角形斜边上的中线
2.【答案】
【知识点】直角三角形的性质
3.【答案】同角的余角相等
【知识点】余角、补角及其性质;直角三角形的性质
4.【答案】6
【知识点】含30°角的直角三角形;直角三角形的性质
5.【答案】
【知识点】尺规作图-垂直平分线;直角三角形斜边上的中线
6.【答案】45
【知识点】余角、补角及其性质;等腰三角形的性质;直角三角形斜边上的中线
7.【答案】A
【知识点】直角三角形的性质
8.【答案】A
【知识点】余角、补角及其性质;直角三角形的性质
9.【答案】D
【知识点】等边三角形的性质;含30°角的直角三角形
10.【答案】D
【知识点】含30°角的直角三角形
11.【答案】D
【知识点】直角三角形的性质
12.【答案】∠ABC所有可能的值为:45°或30°150°
【知识点】含30°角的直角三角形
13.【答案】(1)的周长为14;
(2).
【知识点】三角形内角和定理;等腰三角形的判定与性质;直角三角形斜边上的中线
14.【答案】(1)①12;②2或4
(2)①;②为或或.
【知识点】等腰三角形的判定与性质;等边三角形的性质;含30°角的直角三角形
15.【答案】(1)解:如图1,即为所求;
(2)解:如图2,点Q即为所求;
【知识点】垂线段最短及其应用;直角三角形的性质
16.【答案】(1)解:∵AD⊥BC,
∴在Rt△BAD中,∠BAD+∠B=90°,
又∵∠B=64°,∴∠BAD=26°;
∴在Rt△BAD中,∠DAC+∠C=90°,
又∵∠C=56°,∴∠DAC=34°;
(2)解:∵AD⊥BC,DE平分∠ADB,∴∠BDE=45°,
在△BED中,∠B=64°,∴∠B+∠BDE=109°,
∵∠AED=∠B+∠BDE,
∴∠AED=109°.
【知识点】三角形的外角性质;直角三角形的性质
17.【答案】4
【知识点】直角三角形斜边上的中线
18.【答案】船继续航行50海里与钓鱼岛A的距离最近
【知识点】三角形的外角性质;等腰三角形的判定;含30°角的直角三角形
21世纪教育网(www.21cnjy.com)
1 / 6
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
