第一章直角三角形 章末练习(含答案)
文档属性
| 名称 | 第一章直角三角形 章末练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 509.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章直角三角形
一、填空题
1.如图,在中,是的角平分线,,,过作于点,则 .
2.如图,已知A,B,D在同一条直线上,∠A=∠CBE=90°,AC=BD,∠1=∠2=35°.则∠D的度数为 .
3.如图,点O为直线上一点,当直角在如图所示位置时,平分,平分,若,则的度数为 .
4.如图,,,点D在上,,则的长为 .
5.如图,在中,和的平分线相交于点交于交于,过点作于,在下列结论中:①:②若,,则;③当时,;④若,则.其中正确的结论为 .
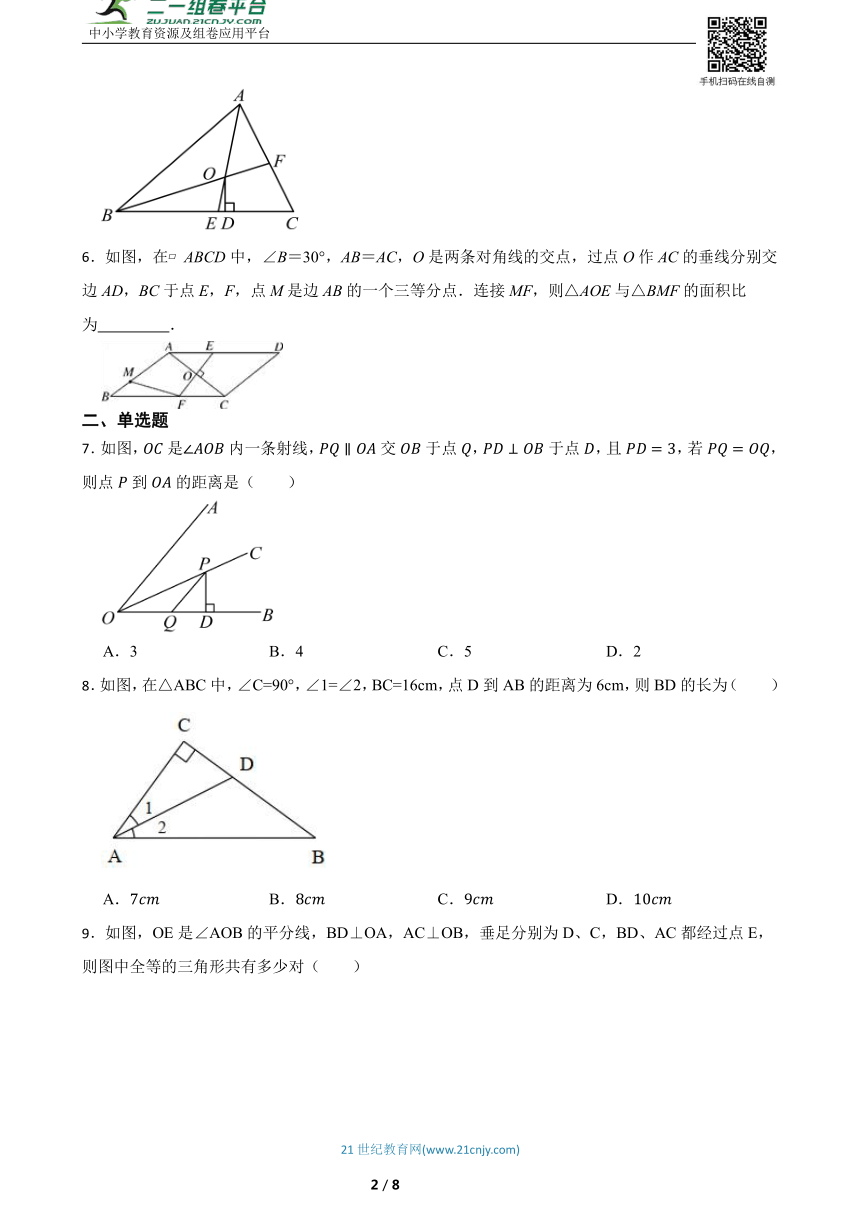
6.如图,在 ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点.连接MF,则△AOE与△BMF的面积比为 .
二、单选题
7.如图,是内一条射线,交于点,于点,且,若,则点到的距离是( )
A.3 B.4 C.5 D.2
8.如图,在△ABC中,∠C=90°,∠1=∠2,BC=16cm,点D到AB的距离为6cm,则BD的长为( )
A. B. C. D.
9.如图,OE是∠AOB的平分线,BD⊥OA,AC⊥OB,垂足分别为D、C,BD、AC都经过点E,则图中全等的三角形共有多少对( )
A.3 B.4 C.5 D.6
10.下列各组数分别为一个三角形三边的长,其中不能构成直角三角形的一组是( )
A. B. C. D.
11.如图,在中,,AD平分,于点E,若,则BE的长为( )
A.5 B. C. D.2
12.如图,在△ABC中,∠C=90°,分别以点A,B为圆心,大于 AB长为半径作弧,两弧分别交于M,N两点,过M,N两点的直线交AC于点E,若AC=8,BC=6,则AE的长为( )
A.2 B.3 C. D.
13.分别以下列四组线段为三边,能构成直角三角形的是( )
A.0.3,0.4,0.5 B.1,1,2
C.1,2,3 D.9,16,25
14.下列四组线段中,能组成直角三角形的是( )
A.a=2,b=3,c=4 B.a=3,b=4,c=5
C.a=4,b=5,c=6 D.a=7,b=8,c=9
15.如图,在Rt中,,于点是的中点,则的长为( )
A.1 B.2 C.3 D.4
16.如图,点E在CA延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:①CEBD;②ABCD;③FQ平分∠AFP;④∠B+∠E=140°;⑤∠QFM=20°.其中结论正确的序号是( )
A.①②③④⑤ B.①②③④ C.②③④ D.①⑤
三、解答题
17.如图:,与相交于点F,.
(1)若平分,求的度数;
(2)若,求的度数.
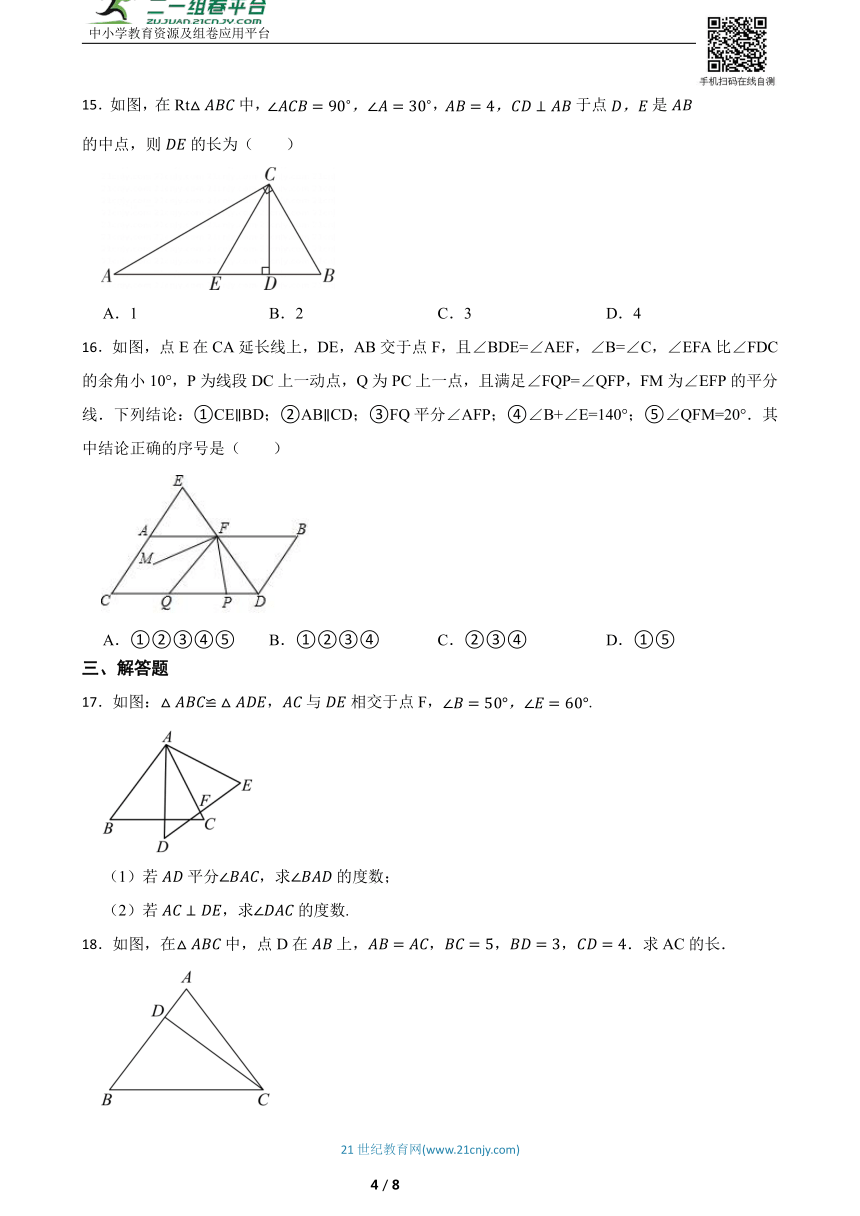
18.如图,在中,点D在上,,,,.求AC的长.
19.有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线,已知门宽4尺,求竹竿高与门高.
20.如图,已知点A、B分别在∠MON的边ON、OM上(不与点O重合),AD平分∠BAN,BC平分∠ABM,直线AD,BC相交于点C.
(1)如图1,若∠MON = 90°,试猜想∠ACB=________ °;
(2)如图2,在(1)的基础上,若∠MON每秒钟变小10°,经过了t秒(0①试用含t的代数式表示∠ACB的度数;
②并求出当t取何值时,∠MON与∠ACB的度数相等;
(3)如图3,在(2)的条件下,若BC平分∠ABO,其它条件不改变,请直接写出∠BCD与∠MON的关系.
四、计算题
21.如图,直线,相交于点,是内一条射线,平分.
(1)若,求的度数.
(2)若比大,求的度数.
22.为弘扬劳动精神,让同学们在实践中体验劳动、认识劳动,从而培养尊重劳动、热爱劳动、尊重劳动人民的品质,学校准备在校园的一角开垦一块如图所示的四边形土地.经测量,,,,,,请计算该四边形土地的面积.
23.若点是射线上异于起点的一点,且,则称点为射线的倍衍生点.例如,在图1中,点在射线上,且,则点为射线的2倍衍生点;点在射线上,且,则点为射线的倍衍生点.
(1)填空:已知,
①若点为射线的3倍衍生点,则 ;
②若点为射线的倍衍生点,则 ;
(2)如图2,已知是等边三角形,点为射线的倍衍生点.
①若点为射线的1倍衍生点,满足,求的值;
②若点是直线上异于点的一点,满足,请直接用含的式子表示.
答案解析部分
1.【答案】2
【知识点】角平分线的性质;含30°角的直角三角形
2.【答案】90°
【知识点】三角形全等及其性质;直角三角形的性质
3.【答案】
【知识点】角的运算;角平分线的性质
4.【答案】
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的判定;勾股定理
5.【答案】②③④
【知识点】三角形内角和定理;三角形的外角性质;角平分线的性质
6.【答案】3∶4
【知识点】三角形的面积;含30°角的直角三角形
7.【答案】A
【知识点】角平分线的性质;等腰三角形的性质;内错角的概念
8.【答案】D
【知识点】角平分线的性质
9.【答案】B
【知识点】三角形全等的判定;角平分线的性质
10.【答案】A
【知识点】勾股定理的逆定理
11.【答案】B
【知识点】角平分线的性质;勾股定理
12.【答案】D
【知识点】线段垂直平分线的性质;勾股定理;尺规作图-垂直平分线
13.【答案】A
【知识点】勾股定理的逆定理
14.【答案】B
【知识点】三角形三边关系;勾股定理的逆定理
15.【答案】A
【知识点】含30°角的直角三角形;直角三角形斜边上的中线
16.【答案】A
【知识点】平行线的判定与性质;角平分线的性质;角平分线的判定
17.【答案】(1)
(2)
【知识点】三角形内角和定理;三角形全等及其性质;角平分线的性质
18.【答案】
【知识点】勾股定理;勾股定理的逆定理
19.【答案】解:设门高为x尺,则竹竿长为(x+1)尺,
根据勾股定理可得:
x2+42=(x+1)2,即x2+16=x2+2x+1,
解得:x=7.5,
故:门高7.5尺,竹竿高=7.5+1=8.5尺.
【知识点】勾股定理的应用
20.【答案】(1)45;(2)①∠ACB =(45+5t)°;②t = 3;(3)∠BCD = ∠MON
【知识点】三角形内角和定理;三角形的外角性质;角平分线的性质
21.【答案】(1)
(2)
【知识点】角的运算;角平分线的性质;对顶角及其性质;邻补角
22.【答案】该四边形土地的面积为
【知识点】勾股定理
23.【答案】(1)①12;②2或4
(2)①;②为或或.
【知识点】等腰三角形的判定与性质;等边三角形的性质;含30°角的直角三角形
21世纪教育网(www.21cnjy.com)
1 / 8
第一章直角三角形
一、填空题
1.如图,在中,是的角平分线,,,过作于点,则 .
2.如图,已知A,B,D在同一条直线上,∠A=∠CBE=90°,AC=BD,∠1=∠2=35°.则∠D的度数为 .
3.如图,点O为直线上一点,当直角在如图所示位置时,平分,平分,若,则的度数为 .
4.如图,,,点D在上,,则的长为 .
5.如图,在中,和的平分线相交于点交于交于,过点作于,在下列结论中:①:②若,,则;③当时,;④若,则.其中正确的结论为 .
6.如图,在 ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点.连接MF,则△AOE与△BMF的面积比为 .
二、单选题
7.如图,是内一条射线,交于点,于点,且,若,则点到的距离是( )
A.3 B.4 C.5 D.2
8.如图,在△ABC中,∠C=90°,∠1=∠2,BC=16cm,点D到AB的距离为6cm,则BD的长为( )
A. B. C. D.
9.如图,OE是∠AOB的平分线,BD⊥OA,AC⊥OB,垂足分别为D、C,BD、AC都经过点E,则图中全等的三角形共有多少对( )
A.3 B.4 C.5 D.6
10.下列各组数分别为一个三角形三边的长,其中不能构成直角三角形的一组是( )
A. B. C. D.
11.如图,在中,,AD平分,于点E,若,则BE的长为( )
A.5 B. C. D.2
12.如图,在△ABC中,∠C=90°,分别以点A,B为圆心,大于 AB长为半径作弧,两弧分别交于M,N两点,过M,N两点的直线交AC于点E,若AC=8,BC=6,则AE的长为( )
A.2 B.3 C. D.
13.分别以下列四组线段为三边,能构成直角三角形的是( )
A.0.3,0.4,0.5 B.1,1,2
C.1,2,3 D.9,16,25
14.下列四组线段中,能组成直角三角形的是( )
A.a=2,b=3,c=4 B.a=3,b=4,c=5
C.a=4,b=5,c=6 D.a=7,b=8,c=9
15.如图,在Rt中,,于点是的中点,则的长为( )
A.1 B.2 C.3 D.4
16.如图,点E在CA延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:①CEBD;②ABCD;③FQ平分∠AFP;④∠B+∠E=140°;⑤∠QFM=20°.其中结论正确的序号是( )
A.①②③④⑤ B.①②③④ C.②③④ D.①⑤
三、解答题
17.如图:,与相交于点F,.
(1)若平分,求的度数;
(2)若,求的度数.
18.如图,在中,点D在上,,,,.求AC的长.
19.有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线,已知门宽4尺,求竹竿高与门高.
20.如图,已知点A、B分别在∠MON的边ON、OM上(不与点O重合),AD平分∠BAN,BC平分∠ABM,直线AD,BC相交于点C.
(1)如图1,若∠MON = 90°,试猜想∠ACB=________ °;
(2)如图2,在(1)的基础上,若∠MON每秒钟变小10°,经过了t秒(0
②并求出当t取何值时,∠MON与∠ACB的度数相等;
(3)如图3,在(2)的条件下,若BC平分∠ABO,其它条件不改变,请直接写出∠BCD与∠MON的关系.
四、计算题
21.如图,直线,相交于点,是内一条射线,平分.
(1)若,求的度数.
(2)若比大,求的度数.
22.为弘扬劳动精神,让同学们在实践中体验劳动、认识劳动,从而培养尊重劳动、热爱劳动、尊重劳动人民的品质,学校准备在校园的一角开垦一块如图所示的四边形土地.经测量,,,,,,请计算该四边形土地的面积.
23.若点是射线上异于起点的一点,且,则称点为射线的倍衍生点.例如,在图1中,点在射线上,且,则点为射线的2倍衍生点;点在射线上,且,则点为射线的倍衍生点.
(1)填空:已知,
①若点为射线的3倍衍生点,则 ;
②若点为射线的倍衍生点,则 ;
(2)如图2,已知是等边三角形,点为射线的倍衍生点.
①若点为射线的1倍衍生点,满足,求的值;
②若点是直线上异于点的一点,满足,请直接用含的式子表示.
答案解析部分
1.【答案】2
【知识点】角平分线的性质;含30°角的直角三角形
2.【答案】90°
【知识点】三角形全等及其性质;直角三角形的性质
3.【答案】
【知识点】角的运算;角平分线的性质
4.【答案】
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的判定;勾股定理
5.【答案】②③④
【知识点】三角形内角和定理;三角形的外角性质;角平分线的性质
6.【答案】3∶4
【知识点】三角形的面积;含30°角的直角三角形
7.【答案】A
【知识点】角平分线的性质;等腰三角形的性质;内错角的概念
8.【答案】D
【知识点】角平分线的性质
9.【答案】B
【知识点】三角形全等的判定;角平分线的性质
10.【答案】A
【知识点】勾股定理的逆定理
11.【答案】B
【知识点】角平分线的性质;勾股定理
12.【答案】D
【知识点】线段垂直平分线的性质;勾股定理;尺规作图-垂直平分线
13.【答案】A
【知识点】勾股定理的逆定理
14.【答案】B
【知识点】三角形三边关系;勾股定理的逆定理
15.【答案】A
【知识点】含30°角的直角三角形;直角三角形斜边上的中线
16.【答案】A
【知识点】平行线的判定与性质;角平分线的性质;角平分线的判定
17.【答案】(1)
(2)
【知识点】三角形内角和定理;三角形全等及其性质;角平分线的性质
18.【答案】
【知识点】勾股定理;勾股定理的逆定理
19.【答案】解:设门高为x尺,则竹竿长为(x+1)尺,
根据勾股定理可得:
x2+42=(x+1)2,即x2+16=x2+2x+1,
解得:x=7.5,
故:门高7.5尺,竹竿高=7.5+1=8.5尺.
【知识点】勾股定理的应用
20.【答案】(1)45;(2)①∠ACB =(45+5t)°;②t = 3;(3)∠BCD = ∠MON
【知识点】三角形内角和定理;三角形的外角性质;角平分线的性质
21.【答案】(1)
(2)
【知识点】角的运算;角平分线的性质;对顶角及其性质;邻补角
22.【答案】该四边形土地的面积为
【知识点】勾股定理
23.【答案】(1)①12;②2或4
(2)①;②为或或.
【知识点】等腰三角形的判定与性质;等边三角形的性质;含30°角的直角三角形
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
