2.2.1平行四边形的性质 同步练习(含答案)
文档属性
| 名称 | 2.2.1平行四边形的性质 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 316.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 09:29:40 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.2.1平行四边形的性质
一、单选题
1.如图,四边形是平行四边形,点E在线段的延长线上,若,则( )
A. B. C. D.
2.如图,在平行四边形中,,相交于点,下列结论正确的是( )
A. B. C. D.
3.已知平行四边形ABCD中,∠B=4∠A,则∠C=( )
A.18° B.36° C.72° D.144°
4.如图,四边形是平行四边形,对角线相交于点,则下列判断正确的是( )
A. B. C. D.
5.如图,在平行四边形ABCD中,E为AD的中点.已知AO=6cm,则AC的长为( )
A.12cm B.10cm
C.18cm D.15cm
二、填空题
6.如图,四边形是平行四边形,且,点A的坐标为,点B的坐标为,则点C的坐标为 .
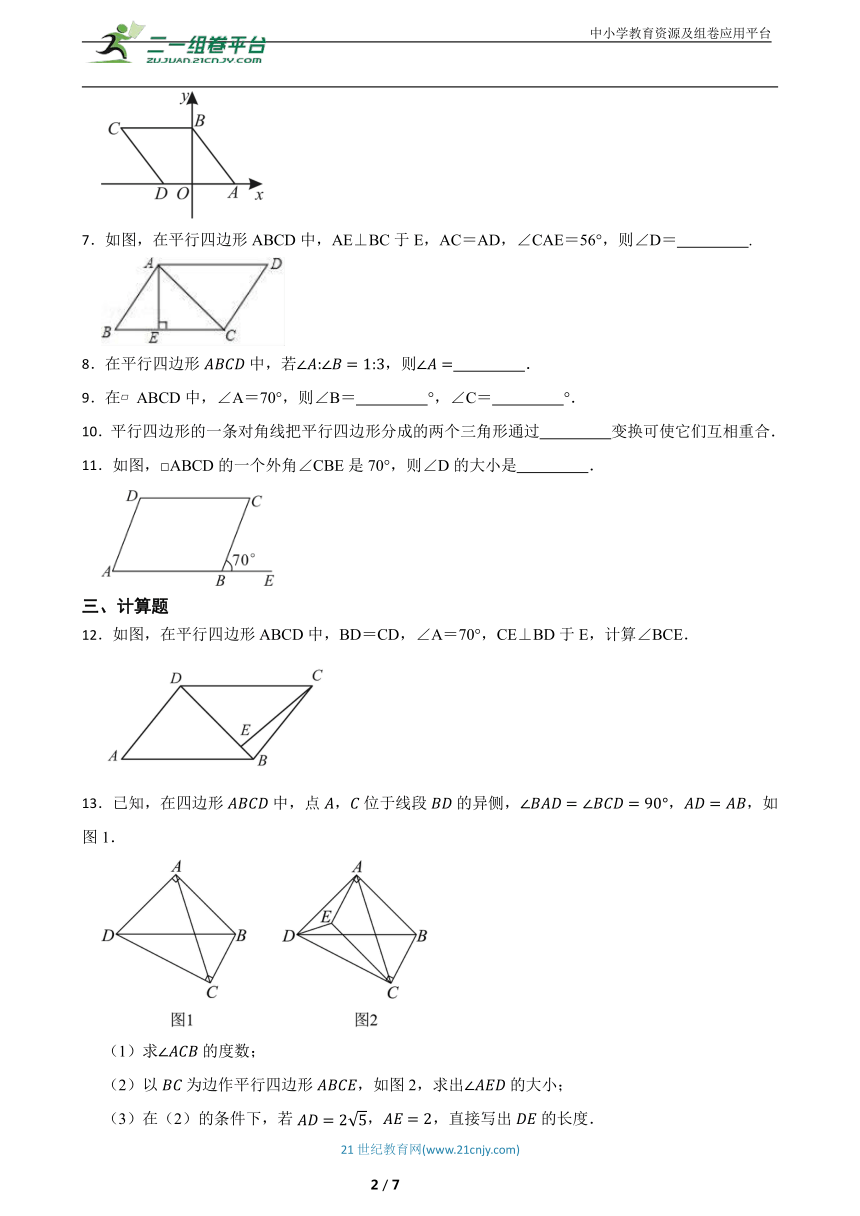
7.如图,在平行四边形ABCD中,AE⊥BC于E,AC=AD,∠CAE=56°,则∠D= .
8.在平行四边形中,若,则 .
9.在 ABCD中,∠A=70°,则∠B= °,∠C= °.
10.平行四边形的一条对角线把平行四边形分成的两个三角形通过 变换可使它们互相重合.
11.如图,□ABCD的一个外角∠CBE是70°,则∠D的大小是 .
三、计算题
12.如图,在平行四边形ABCD中,BD=CD,∠A=70°,CE⊥BD于E,计算∠BCE.
13.已知,在四边形中,点,位于线段的异侧,,,如图1.
(1)求的度数;
(2)以为边作平行四边形,如图2,求出的大小;
(3)在(2)的条件下,若,,直接写出的长度.
四、解答题
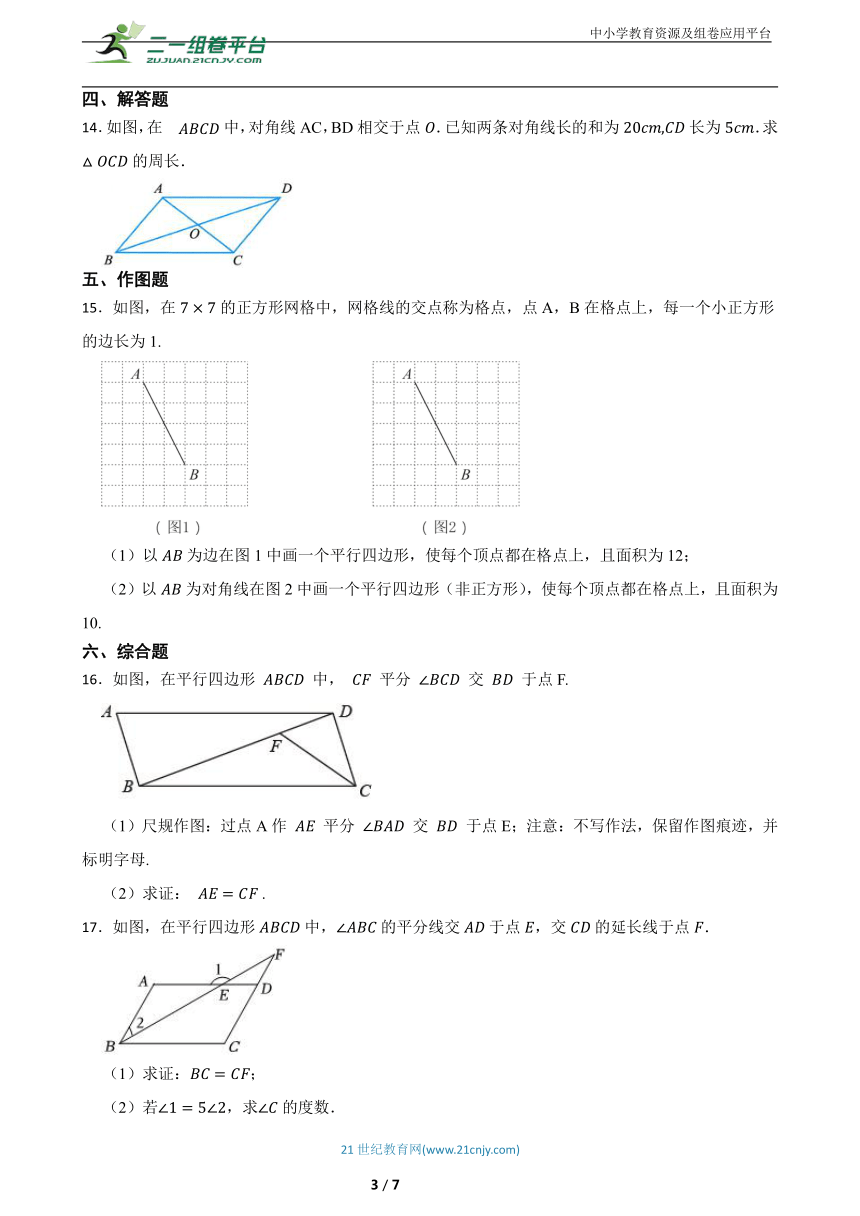
14.如图,在中,对角线AC,BD相交于点.已知两条对角线长的和为长为.求的周长.
五、作图题
15.如图,在的正方形网格中,网格线的交点称为格点,点A,B在格点上,每一个小正方形的边长为1.
(1)以为边在图1中画一个平行四边形,使每个顶点都在格点上,且面积为12;
(2)以为对角线在图2中画一个平行四边形(非正方形),使每个顶点都在格点上,且面积为10.
六、综合题
16.如图,在平行四边形 中, 平分 交 于点F.
(1)尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.
(2)求证: .
17.如图,在平行四边形中,的平分线交于点,交的延长线于点.
(1)求证:;
(2)若,求的度数.
18.如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,AB=6,求四边形BEDF的周长.
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】
7.【答案】73°
8.【答案】
9.【答案】110;70
10.【答案】旋转
11.【答案】110°
12.【答案】20°
13.【答案】(1)
(2)
(3)
14.【答案】解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵AC+BD=20cm,
∴OC+OD=AC+BD=(AC+BD)=10cm,
∵CD=5cm,
∴△OCD的周长为OC+OD+CD=15cm.
15.【答案】(1)解:如图1,四边形ABCD即为所求;
(2)解:如图2,四边形ACBD即为所求;
16.【答案】(1)解:如图,AE为所作;
(2)证明:∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE BAD,∠DCF ∠BCD,
∵四边形ABCD为平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵AB∥CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AE=CF.
17.【答案】(1)证明:四边形是平行四边形,
,
,
平分,
,
,
;
(2)解:平分,
,∠ABC=2∠2,
∵四边形ABCD是平行四边形,
,
,
,,
,
,
.
四边形ABCD是平行四边形,
,
,
.
18.【答案】(1)证明:在 ABCD中,∵AD=CB,AB=CD,∠A=∠C,
又∵E,F分别为边AB,CD的中点,
∴AE=CF,
∴△ADE≌△CBF
(2)解:∵∠ADB=90°,
∴△ABD,△CDB都是直角三角形,
∵AE=EB,CF=DF,
∴DE=BE= AB,BF=DF= CD,
∴DE=BE=BF=DF=3,
∴四边形DEBF是菱形,周长为12.
21世纪教育网(www.21cnjy.com)
2 / 7
2.2.1平行四边形的性质
一、单选题
1.如图,四边形是平行四边形,点E在线段的延长线上,若,则( )
A. B. C. D.
2.如图,在平行四边形中,,相交于点,下列结论正确的是( )
A. B. C. D.
3.已知平行四边形ABCD中,∠B=4∠A,则∠C=( )
A.18° B.36° C.72° D.144°
4.如图,四边形是平行四边形,对角线相交于点,则下列判断正确的是( )
A. B. C. D.
5.如图,在平行四边形ABCD中,E为AD的中点.已知AO=6cm,则AC的长为( )
A.12cm B.10cm
C.18cm D.15cm
二、填空题
6.如图,四边形是平行四边形,且,点A的坐标为,点B的坐标为,则点C的坐标为 .
7.如图,在平行四边形ABCD中,AE⊥BC于E,AC=AD,∠CAE=56°,则∠D= .
8.在平行四边形中,若,则 .
9.在 ABCD中,∠A=70°,则∠B= °,∠C= °.
10.平行四边形的一条对角线把平行四边形分成的两个三角形通过 变换可使它们互相重合.
11.如图,□ABCD的一个外角∠CBE是70°,则∠D的大小是 .
三、计算题
12.如图,在平行四边形ABCD中,BD=CD,∠A=70°,CE⊥BD于E,计算∠BCE.
13.已知,在四边形中,点,位于线段的异侧,,,如图1.
(1)求的度数;
(2)以为边作平行四边形,如图2,求出的大小;
(3)在(2)的条件下,若,,直接写出的长度.
四、解答题
14.如图,在中,对角线AC,BD相交于点.已知两条对角线长的和为长为.求的周长.
五、作图题
15.如图,在的正方形网格中,网格线的交点称为格点,点A,B在格点上,每一个小正方形的边长为1.
(1)以为边在图1中画一个平行四边形,使每个顶点都在格点上,且面积为12;
(2)以为对角线在图2中画一个平行四边形(非正方形),使每个顶点都在格点上,且面积为10.
六、综合题
16.如图,在平行四边形 中, 平分 交 于点F.
(1)尺规作图:过点A作 平分 交 于点E;注意:不写作法,保留作图痕迹,并标明字母.
(2)求证: .
17.如图,在平行四边形中,的平分线交于点,交的延长线于点.
(1)求证:;
(2)若,求的度数.
18.如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,AB=6,求四边形BEDF的周长.
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】
7.【答案】73°
8.【答案】
9.【答案】110;70
10.【答案】旋转
11.【答案】110°
12.【答案】20°
13.【答案】(1)
(2)
(3)
14.【答案】解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵AC+BD=20cm,
∴OC+OD=AC+BD=(AC+BD)=10cm,
∵CD=5cm,
∴△OCD的周长为OC+OD+CD=15cm.
15.【答案】(1)解:如图1,四边形ABCD即为所求;
(2)解:如图2,四边形ACBD即为所求;
16.【答案】(1)解:如图,AE为所作;
(2)证明:∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE BAD,∠DCF ∠BCD,
∵四边形ABCD为平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵AB∥CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AE=CF.
17.【答案】(1)证明:四边形是平行四边形,
,
,
平分,
,
,
;
(2)解:平分,
,∠ABC=2∠2,
∵四边形ABCD是平行四边形,
,
,
,,
,
,
.
四边形ABCD是平行四边形,
,
,
.
18.【答案】(1)证明:在 ABCD中,∵AD=CB,AB=CD,∠A=∠C,
又∵E,F分别为边AB,CD的中点,
∴AE=CF,
∴△ADE≌△CBF
(2)解:∵∠ADB=90°,
∴△ABD,△CDB都是直角三角形,
∵AE=EB,CF=DF,
∴DE=BE= AB,BF=DF= CD,
∴DE=BE=BF=DF=3,
∴四边形DEBF是菱形,周长为12.
21世纪教育网(www.21cnjy.com)
2 / 7
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
