宁夏回族自治区石嘴山市2024-2025学年高三上学期1月期末考试数学试题(无答案)
文档属性
| 名称 | 宁夏回族自治区石嘴山市2024-2025学年高三上学期1月期末考试数学试题(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 178.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 20:21:37 | ||
图片预览



文档简介
石嘴山2025 届高三期末考试数学试题
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合A={1,2,3,4,5}, B={1,3,5,7,9}, 则A∩B=
A. {1,2,3} B. {1,3,5} C. {2,4,6} D. {3,4,5}
2.已知复数z满足 则复数z在复平面表示的点位于第 象限.
A. 一 B. 二 C. 三 D. 四
3.已知向量 且 则λ=
B. C. D. 2
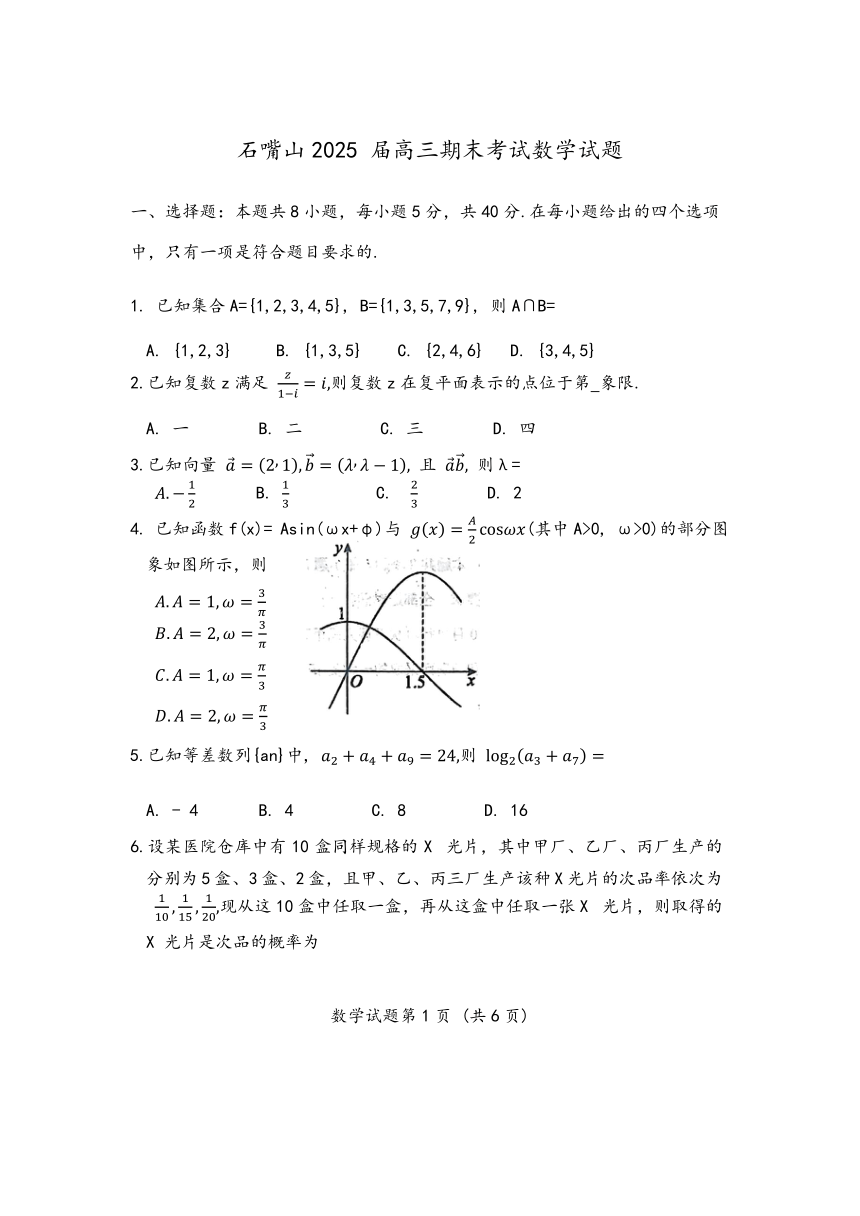
4. 已知函数f(x)= Asin(ωx+φ)与 (其中A>0, ω>0)的部分图象如图所示,则
5.已知等差数列{an}中, 则
A. - 4 B. 4 C. 8 D. 16
6.设某医院仓库中有10盒同样规格的X 光片,其中甲厂、乙厂、丙厂生产的分别为5盒、3盒、2盒,且甲、乙、丙三厂生产该种X光片的次品率依次为 现从这10盒中任取一盒,再从这盒中任取一张X 光片,则取得的X 光片是次品的概率为
数学试题第1页 (共6页)
D.
7.某驾驶员喝了m升酒后,血液中的酒精含量f(x)(毫克/毫升)随时间x(小时)变化的规律近似满足表达式 《酒后驾车与醉酒驾车的标准及相应的处罚》规定:驾驶员血液中酒精含量不得超过0.02毫克/毫升.此驾驶员至少要过 小时后才能开车(不足1小时部分算1小时,结果精确到1小时).
A. 2 B. 3 C. 4 D. 5
8.已知椭圆 与双曲线 有公共焦点,F为右焦点,O为坐标原点,双曲线的一条渐近线与椭圆在第一象限交于点P,且满足OP⊥FP,则椭圆的离心率为
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.2024年10月央行再次下调人民币存款利率,存款利率下调是为了刺激经济增长促进投资和消费而采取的一种货币政策.下表为某银行近年来的人民币一年定期存款利率:
时间 2018年 2019年 2020年 2021年 2022年 2024年 2024年
利率/% 1.35 1.50 1.75 1.75 1.55 1,35 1.10
关于表中的7个存款利率数据,下列结论正确的是
A. 极差为0.25
B.平均数不大于1.5
C.20%分位数与30%分位数相等
D. 中位数为1.50
数 学 试 题 第 2 页 (共6 页)
10.下列结论正确的是
B. 若aC. 若x(x-2)<0, 则
D. 若a>0, b>0, a+b≤1, 则
11. 如图,在四棱锥P--ABCD中, 底面ABCD是边长为2的正方形, 侧面PAD是正三角形,侧面PAD⊥底面ABCD,M是PD的中点,且四棱锥P--ABCD的各个顶点都在球O的球面上,则
A. P、B、C、M 四点共面
B. 平面ABM⊥平面PCD
C.球O的表面积为
D. 直线PC与平面ABM 所成角为45°
三、填空题:本题共3小题,每小题5分,共15分.
的展开式中x 的系数是 .
13. 已知数列{an}的前n项和为 Sn, 若 则
14.已知函数 则函数 的零点个数是 .
数 学 试 题 第 3页 (共6 页)
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知△ABC中, 内角A, B, C所对的边分别为a, b, c,且a:b:c=2:3:4.
(1) 求cosA;
(2) 若点D为AB的中点, 且 ,求△ABC的面积.
16.(15分)
甲、乙两人进行羽毛球比赛、双方约定采用五局三胜制(有一方先胜三局即赢得比赛,比赛结束),根据双方以往的比赛情况可知每局比赛甲获胜的概率是 ,乙获胜的概率是 .假设每局比赛结果互不影响。
(1)求比赛进行四局且甲获胜的概率;
(2)比赛结束时、甲、乙共进行了X局比赛,求X的分布列和期望.
数学 试 题 第4 页 (共6 页)
17.(15分)
如图,在三棱柱ABC-A B C 中, AA ⊥平面ABC, △ABC是等边三角形, 且D为棱AB 的中点.
(1) 证明: BC //平面A CD;
(2) 证明: AB⊥平面CC D;
(3) 若 求平面A CD 与平面ABC 所成角的余弦值.
18.(17分)
在平面内,动点M 到点(1,0)的距离和它到直线x+1=0的距离相等,记动点M 的轨迹为曲线C.
(1)求曲线C的方程,并判断其形状;
(2) 若点. 在曲线C上,且
(i)证明:直线AB过定点:
(ii)记(i)中的直线AB过的定点为P,且过P作垂直于AB的直线l交曲线C于D、E两点,求四边形ADBE的面积的最小值.
数学试题第 5 页 (共6页)
19.(17分)
已知函数
(1)当a=1时, 求曲线y=f(x)的斜率为1的切线方程;
(2)讨论f(x)的单调性;
(3)若f(x)有两个极值点x ,x ,记过两点B(x ,f(x )), C(x ,f(x ))的直线的斜率为k,是否存在实数a,使得k=2-a 若存在,求a的值,若不存在,试说明理由。
数 学试 题第6页 (共6 页)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合A={1,2,3,4,5}, B={1,3,5,7,9}, 则A∩B=
A. {1,2,3} B. {1,3,5} C. {2,4,6} D. {3,4,5}
2.已知复数z满足 则复数z在复平面表示的点位于第 象限.
A. 一 B. 二 C. 三 D. 四
3.已知向量 且 则λ=
B. C. D. 2
4. 已知函数f(x)= Asin(ωx+φ)与 (其中A>0, ω>0)的部分图象如图所示,则
5.已知等差数列{an}中, 则
A. - 4 B. 4 C. 8 D. 16
6.设某医院仓库中有10盒同样规格的X 光片,其中甲厂、乙厂、丙厂生产的分别为5盒、3盒、2盒,且甲、乙、丙三厂生产该种X光片的次品率依次为 现从这10盒中任取一盒,再从这盒中任取一张X 光片,则取得的X 光片是次品的概率为
数学试题第1页 (共6页)
D.
7.某驾驶员喝了m升酒后,血液中的酒精含量f(x)(毫克/毫升)随时间x(小时)变化的规律近似满足表达式 《酒后驾车与醉酒驾车的标准及相应的处罚》规定:驾驶员血液中酒精含量不得超过0.02毫克/毫升.此驾驶员至少要过 小时后才能开车(不足1小时部分算1小时,结果精确到1小时).
A. 2 B. 3 C. 4 D. 5
8.已知椭圆 与双曲线 有公共焦点,F为右焦点,O为坐标原点,双曲线的一条渐近线与椭圆在第一象限交于点P,且满足OP⊥FP,则椭圆的离心率为
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.2024年10月央行再次下调人民币存款利率,存款利率下调是为了刺激经济增长促进投资和消费而采取的一种货币政策.下表为某银行近年来的人民币一年定期存款利率:
时间 2018年 2019年 2020年 2021年 2022年 2024年 2024年
利率/% 1.35 1.50 1.75 1.75 1.55 1,35 1.10
关于表中的7个存款利率数据,下列结论正确的是
A. 极差为0.25
B.平均数不大于1.5
C.20%分位数与30%分位数相等
D. 中位数为1.50
数 学 试 题 第 2 页 (共6 页)
10.下列结论正确的是
B. 若a
D. 若a>0, b>0, a+b≤1, 则
11. 如图,在四棱锥P--ABCD中, 底面ABCD是边长为2的正方形, 侧面PAD是正三角形,侧面PAD⊥底面ABCD,M是PD的中点,且四棱锥P--ABCD的各个顶点都在球O的球面上,则
A. P、B、C、M 四点共面
B. 平面ABM⊥平面PCD
C.球O的表面积为
D. 直线PC与平面ABM 所成角为45°
三、填空题:本题共3小题,每小题5分,共15分.
的展开式中x 的系数是 .
13. 已知数列{an}的前n项和为 Sn, 若 则
14.已知函数 则函数 的零点个数是 .
数 学 试 题 第 3页 (共6 页)
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知△ABC中, 内角A, B, C所对的边分别为a, b, c,且a:b:c=2:3:4.
(1) 求cosA;
(2) 若点D为AB的中点, 且 ,求△ABC的面积.
16.(15分)
甲、乙两人进行羽毛球比赛、双方约定采用五局三胜制(有一方先胜三局即赢得比赛,比赛结束),根据双方以往的比赛情况可知每局比赛甲获胜的概率是 ,乙获胜的概率是 .假设每局比赛结果互不影响。
(1)求比赛进行四局且甲获胜的概率;
(2)比赛结束时、甲、乙共进行了X局比赛,求X的分布列和期望.
数学 试 题 第4 页 (共6 页)
17.(15分)
如图,在三棱柱ABC-A B C 中, AA ⊥平面ABC, △ABC是等边三角形, 且D为棱AB 的中点.
(1) 证明: BC //平面A CD;
(2) 证明: AB⊥平面CC D;
(3) 若 求平面A CD 与平面ABC 所成角的余弦值.
18.(17分)
在平面内,动点M 到点(1,0)的距离和它到直线x+1=0的距离相等,记动点M 的轨迹为曲线C.
(1)求曲线C的方程,并判断其形状;
(2) 若点. 在曲线C上,且
(i)证明:直线AB过定点:
(ii)记(i)中的直线AB过的定点为P,且过P作垂直于AB的直线l交曲线C于D、E两点,求四边形ADBE的面积的最小值.
数学试题第 5 页 (共6页)
19.(17分)
已知函数
(1)当a=1时, 求曲线y=f(x)的斜率为1的切线方程;
(2)讨论f(x)的单调性;
(3)若f(x)有两个极值点x ,x ,记过两点B(x ,f(x )), C(x ,f(x ))的直线的斜率为k,是否存在实数a,使得k=2-a 若存在,求a的值,若不存在,试说明理由。
数 学试 题第6页 (共6 页)
同课章节目录
