23.3.1 相似三角形 (新课PPT共20张)
文档属性
| 名称 | 23.3.1 相似三角形 (新课PPT共20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 722.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-25 23:58:42 | ||
图片预览






文档简介
课件20张PPT。23.3.1 相似三角形知识回顾 1、什么叫相似多边形呢?
相似多边形有什么性质?2、你能类似的给相似三角形下一个定义吗?概念类比 1、各角对应相等,各边对应成比例的两个多边形
叫相似多边形2、三个角对应相等,三条边边对应成比例的两个
三角形 叫相似三角形
相似三角形对应边的比,叫做相似比
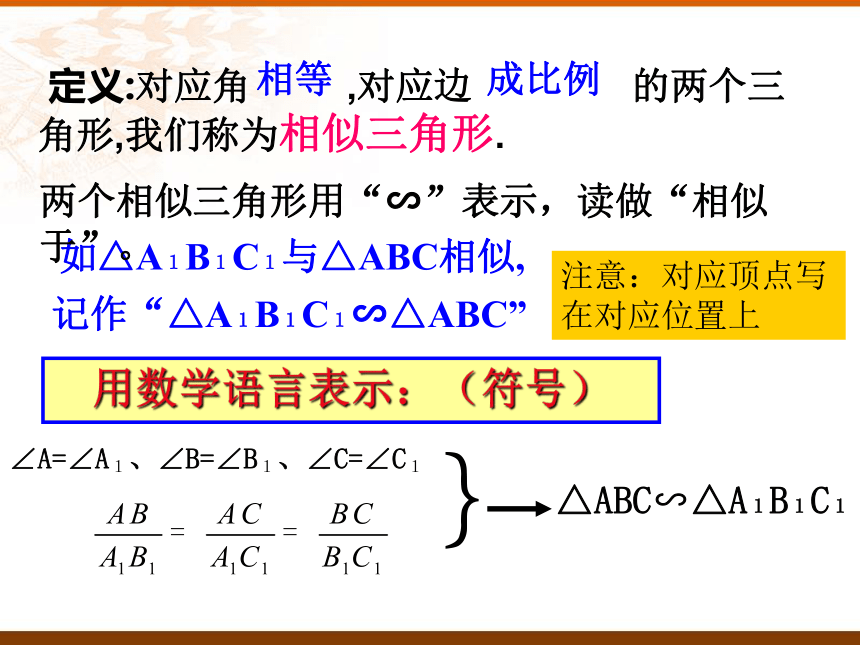
定义:对应角 ,对应边 的两个三角形,我们称为相似三角形.∠A=∠A1、∠B=∠B1、∠C=∠C1用数学语言表示:(符号)如△A1B1C1与△ABC相似,注意:对应顶点写 在对应位置上记作“△A1B1C1∽△ABC”
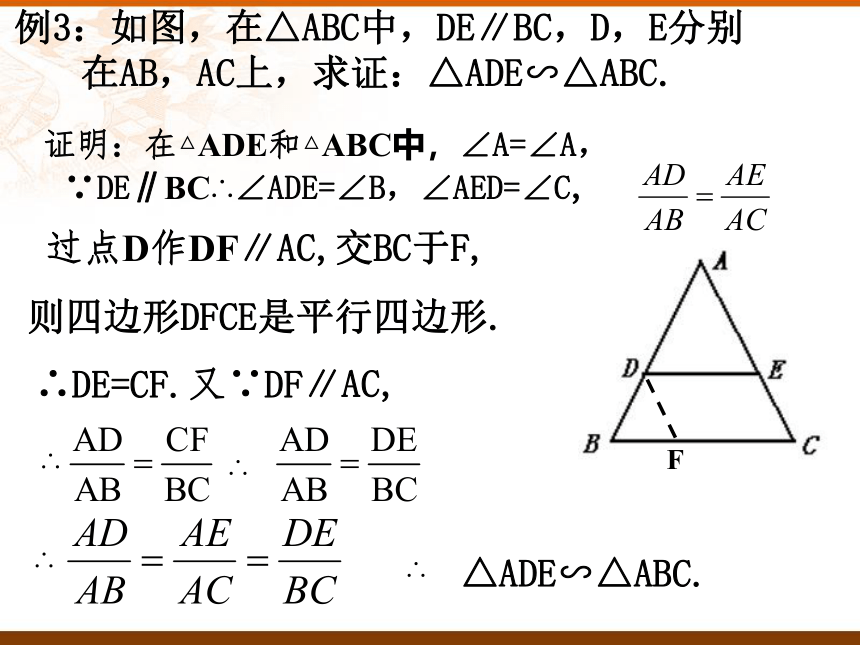
相等成比例两个相似三角形用“∽”表示,读做“相似于”。例3:如图,在△ABC中,DE∥BC,D,E分别在AB,AC上,求证:△ADE∽△ABC.F证明:在△ADE和△ABC中,∠A=∠A,∵DE∥BC∴∠ADE=∠B,∠AED=∠C,过点D作DF∥AC,交BC于F,
则四边形DFCE是平行四边形.∴DE=CF.又∵DF∥AC,∴∴∴△ADE∽△ABC.∴相似三角形判定预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A型图X型图下面这两个三角形相似吗?ABCDEF84642360°80°40 °60 °40 °80 °
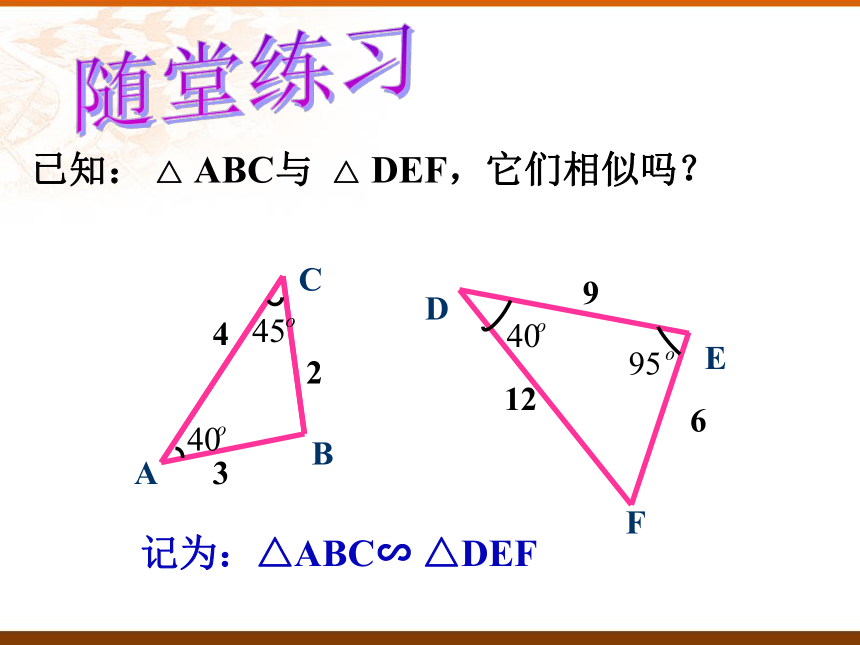
已知: △ ABC与 △ DEF,它们相似吗?记为:△ABC∽ △DEF随堂练习相似三角形判定预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A型图X型图由上面 结论完成下列各题:
1、若 ?ABC∽?DEF, 则?A=____,
____= ? E, ?C= ____,
2、若?A1B1C1 ∽?A2B2C2 ,且A1C1 =2,A2C2 =6,
则?A1B1C1 与?A2B2C2 的相似比是_____。
如果?ABC∽?DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系 ?对应边呢?什么是相似比? 相似三角形对应角相等,对应边成比例。对应边的比为相似比。 ∠D∠B∠FDEACEF想 一想小组讨论,领悟新知1、两个全等三角形一定相似吗?为什么?
2、两个直角三角形一定相似吗?为什么?两个等腰直角三角形呢?随堂练习,巩固新知1、在下面的两组图形中,各有两个相似三角形,试确定x , y , m , n 的值。 一、二、请同学们细心判一判 1、如果两个三角形全等,则它们必相似。√2、若两个三角形相似,且相似比为1,则它们必全等。√3、如果两个三角形与第三个等腰直角三角形相似,则这两个三角形必相似。√4、相似的两个三角形一定大小不等。×如图,有一块呈三角形形状的草坪,其中 一边的长是20m,在这个草坪的图纸上,这条边 长5cm,其他两边的长度都是3.5cm。求该草坪 其他两边的实际长度。解:20m=2000cm
设其他两边的实际长度都是x cm, 解得:所以,草坪其他两边的实际长度都是14m动动手,练一练例1XX3.5cm3.5cm20m5㎝例2、如图,已知△ ABC∽ △ADE,AE=50cm,EC=30cm,BC=70cm,
∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长。运用知识,拓展思维50cm30cm45040070cm在例2的条件下,有哪些线段成比例?图中有互相平行的线段吗?为什么?运用知识,拓展思维从图象中观察并找出下列各对相似三角形的对应角和对应边:图2ABCDEF△ABC∽△ACD△AOC∽△BOD△ABC∽△EDF图3归纳提升本节课你学习到了哪些东西?
△ABC 的各边之比是2:5:6,与其相似的另一个 的最大边为18cm,那么它的最小边长是多少?想一想30 °20 °45°45°45°45°1155直角三角形等腰直角三角形
相似多边形有什么性质?2、你能类似的给相似三角形下一个定义吗?概念类比 1、各角对应相等,各边对应成比例的两个多边形
叫相似多边形2、三个角对应相等,三条边边对应成比例的两个
三角形 叫相似三角形
相似三角形对应边的比,叫做相似比
定义:对应角 ,对应边 的两个三角形,我们称为相似三角形.∠A=∠A1、∠B=∠B1、∠C=∠C1用数学语言表示:(符号)如△A1B1C1与△ABC相似,注意:对应顶点写 在对应位置上记作“△A1B1C1∽△ABC”
相等成比例两个相似三角形用“∽”表示,读做“相似于”。例3:如图,在△ABC中,DE∥BC,D,E分别在AB,AC上,求证:△ADE∽△ABC.F证明:在△ADE和△ABC中,∠A=∠A,∵DE∥BC∴∠ADE=∠B,∠AED=∠C,过点D作DF∥AC,交BC于F,
则四边形DFCE是平行四边形.∴DE=CF.又∵DF∥AC,∴∴∴△ADE∽△ABC.∴相似三角形判定预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A型图X型图下面这两个三角形相似吗?ABCDEF84642360°80°40 °60 °40 °80 °
已知: △ ABC与 △ DEF,它们相似吗?记为:△ABC∽ △DEF随堂练习相似三角形判定预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A型图X型图由上面 结论完成下列各题:
1、若 ?ABC∽?DEF, 则?A=____,
____= ? E, ?C= ____,
2、若?A1B1C1 ∽?A2B2C2 ,且A1C1 =2,A2C2 =6,
则?A1B1C1 与?A2B2C2 的相似比是_____。
如果?ABC∽?DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系 ?对应边呢?什么是相似比? 相似三角形对应角相等,对应边成比例。对应边的比为相似比。 ∠D∠B∠FDEACEF想 一想小组讨论,领悟新知1、两个全等三角形一定相似吗?为什么?
2、两个直角三角形一定相似吗?为什么?两个等腰直角三角形呢?随堂练习,巩固新知1、在下面的两组图形中,各有两个相似三角形,试确定x , y , m , n 的值。 一、二、请同学们细心判一判 1、如果两个三角形全等,则它们必相似。√2、若两个三角形相似,且相似比为1,则它们必全等。√3、如果两个三角形与第三个等腰直角三角形相似,则这两个三角形必相似。√4、相似的两个三角形一定大小不等。×如图,有一块呈三角形形状的草坪,其中 一边的长是20m,在这个草坪的图纸上,这条边 长5cm,其他两边的长度都是3.5cm。求该草坪 其他两边的实际长度。解:20m=2000cm
设其他两边的实际长度都是x cm, 解得:所以,草坪其他两边的实际长度都是14m动动手,练一练例1XX3.5cm3.5cm20m5㎝例2、如图,已知△ ABC∽ △ADE,AE=50cm,EC=30cm,BC=70cm,
∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长。运用知识,拓展思维50cm30cm45040070cm在例2的条件下,有哪些线段成比例?图中有互相平行的线段吗?为什么?运用知识,拓展思维从图象中观察并找出下列各对相似三角形的对应角和对应边:图2ABCDEF△ABC∽△ACD△AOC∽△BOD△ABC∽△EDF图3归纳提升本节课你学习到了哪些东西?
△ABC 的各边之比是2:5:6,与其相似的另一个 的最大边为18cm,那么它的最小边长是多少?想一想30 °20 °45°45°45°45°1155直角三角形等腰直角三角形
