2.5.2矩形的判定 同步练习(含答案)
文档属性
| 名称 | 2.5.2矩形的判定 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 291.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.5.2矩形的判定
一、单选题
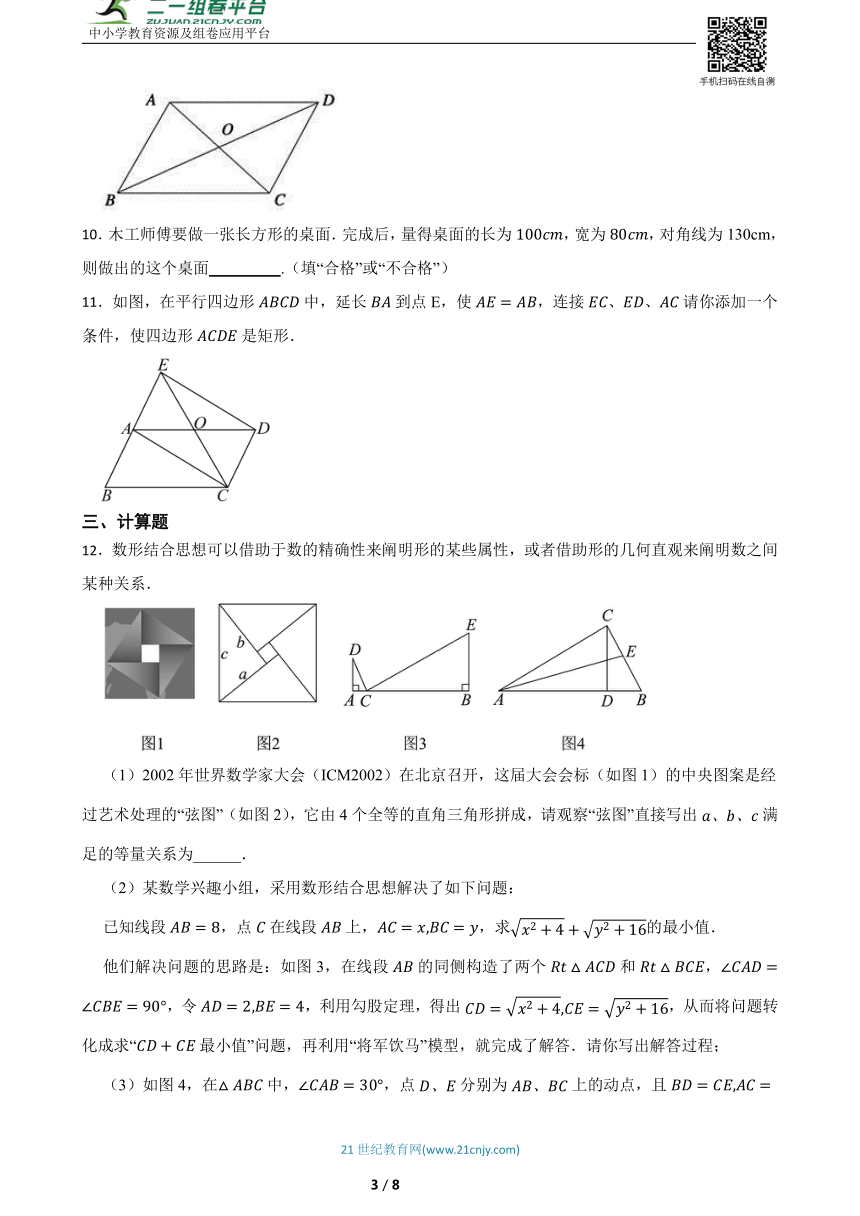
1.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( ).
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
2.已知的对角线相交于点O,若要使成为矩形,可添加下列哪个条件( )
A. B. C. D.
3.如图,四边形中,,,,,将边绕点逆时针方向旋转90°至,连接,则的面积为( )
A.3 B.4 C.5 D.6
4.如图,平行四边形的对角线,相交于点,且,点为边上一动点(不与点A,重合),于点,于点,若,,则的最小值为( )
A.3 B.2 C. D.
5.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF。在:下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形。其中正确的是( )
A.①④ B.①② C.①②③ D.②③④
二、填空题
6.如图,中,,,,将绕点C顺时针旋转,得到,A、B的对应点分别为、,当时,则的长为 .
7.如图,在中,,且,,点是斜边上的一个动点,过点分别作于点,于点,连接,则线段的最小值为 .
8.如图,创新小组要测量公园内一棵树AB的高度,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为45°,已知测角仪的架高CE=1.2米,则这棵树的高度为 米.
9.如图,四边形ABCD是平行四边形,添加一个条件: ,可使它成为矩形.
10.木工师傅要做一张长方形的桌面.完成后,量得桌面的长为,宽为,对角线为130cm,则做出的这个桌面 .(填“合格”或“不合格”)
11.如图,在平行四边形中,延长到点E,使,连接、、请你添加一个条件,使四边形是矩形.
三、计算题
12.数形结合思想可以借助于数的精确性来阐明形的某些属性,或者借助形的几何直观来阐明数之间某种关系.
(1)2002年世界数学家大会(ICM2002)在北京召开,这届大会会标(如图1)的中央图案是经过艺术处理的“弦图”(如图2),它由4个全等的直角三角形拼成,请观察“弦图”直接写出满足的等量关系为______.
(2)某数学兴趣小组,采用数形结合思想解决了如下问题:
已知线段,点在线段上,,求的最小值.
他们解决问题的思路是:如图3,在线段的同侧构造了两个和,,令,利用勾股定理,得出,从而将问题转化成求“最小值”问题,再利用“将军饮马”模型,就完成了解答.请你写出解答过程;
(3)如图4,在中,,点分别为上的动点,且,求的最小值.
四、解答题
13.如图,在四边形中,,,,,点P从点D出发,以每秒1个单位长度的速度向点A运动,点Q从点B同时出发,以每秒2个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P运动时间为t秒.
(1)当点P运动停止时,______,线段的长为______;
(2)①用含t的式子填空:______,______,______;
② t为何值时,四边形为矩形,求出t的值;
(3)在运动的过程中,是否存在某一时刻t,使以P,D,C,Q为顶点的四边形为平行四边形?若存在,请求出t的值,若不存在,请说明理由.
五、综合题
14. ABCD中,过点D作DE⊥AB于点E,点F在CD上,DF=BE,连接:BF,AF。
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE-3,DF=5,求矩形BFDE的面积。
15.如图, ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,无需说明理由.
16.如图,在△ABC中,点O是AC边上一动点,过点O作DE,使DE∥BC,DE交∠ACB的角平分线于点D,交∠ACB的外角平分线于点E.
(1)求证:OD=OE;
(2)当点O运动到何处时,四边形CDAE是矩形 请证明你的结论.
答案解析部分
1.【答案】C
【知识点】矩形的判定
2.【答案】C
【知识点】矩形的判定
3.【答案】A
【知识点】矩形的判定与性质;旋转的性质
4.【答案】C
【知识点】垂线段最短及其应用;勾股定理;矩形的判定与性质
5.【答案】A
【知识点】平行线的性质;角平分线的性质;矩形的判定;直角三角形的性质
6.【答案】
【知识点】勾股定理;矩形的判定与性质;旋转的性质
7.【答案】
【知识点】勾股定理;矩形的判定与性质
8.【答案】11.2
【知识点】等腰三角形的判定与性质;矩形的判定与性质;线段的和、差、倍、分的简单计算
9.【答案】∠ABC=90°(或AC=BD等)
【知识点】矩形的判定
10.【答案】不合格
【知识点】勾股定理的逆定理;矩形的判定
11.【答案】(答案不唯一)
【知识点】矩形的判定
12.【答案】(1);
(2)的最小值为;
(3)的最小值为.
【知识点】勾股定理;矩形的判定与性质;轴对称的性质
13.【答案】(1);
(2)①;;;②
(3)
【知识点】平行四边形的性质;矩形的判定;一元一次方程的实际应用-几何问题
14.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形
∵DE⊥AB,∴∠DEB=90°,
∴四边形BFDE是矩形
(2)解:∵AB∥CD,
∴∠BAF=∠DFA,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠DFA=∠DAF,
∴AD=DF=5,
∵DE⊥AB,
∴∠AED=90°,由勾股定理得:DE= =4,
∴矩形BFDE的面积=DF×DE=5×4=20
【知识点】矩形的判定
15.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,∴OE=OF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(SAS).
(2)解:四边形EBFD是矩形;
理由如下:
∵OB=OD,OE=OF,∴四边形EBFD是平行四边形,∵BD=EF,∴四边形EBFD是矩形.
【知识点】全等三角形的判定与性质;平行四边形的性质;矩形的判定
16.【答案】(1)解:∵DE∥BC
∴∠ODC=∠DCB
又CD平分∠ACB
∴∠OCD=∠DCB
∴∠ODC=∠OCD
∴OD=OC
同理,OE=OC
∴OD=OE
(2)解:当点O运动到AC的中点时,四边形CDAE是矩形.
∵O为AC的中点
∴OA=OC
又OD=OE
∴四边形CDAE是平行四边形
又∵CD平分∠ACB,CE平分∠ACF
∴∠OCD+∠OCE=90°
即∠DCE=90°
∴四边形CDAE是矩形
【知识点】等式的基本性质;等腰三角形的性质;矩形的判定;角平分线的概念
21世纪教育网(www.21cnjy.com)
2 / 8
2.5.2矩形的判定
一、单选题
1.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( ).
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
2.已知的对角线相交于点O,若要使成为矩形,可添加下列哪个条件( )
A. B. C. D.
3.如图,四边形中,,,,,将边绕点逆时针方向旋转90°至,连接,则的面积为( )
A.3 B.4 C.5 D.6
4.如图,平行四边形的对角线,相交于点,且,点为边上一动点(不与点A,重合),于点,于点,若,,则的最小值为( )
A.3 B.2 C. D.
5.如图,在锐角△ABC中,延长BC到点D,点O是AC边上的一个动点,过点O作直线MN∥BC,MN分别交∠ACB、∠ACD的平分线于E,F两点,连接AE、AF。在:下列结论中:①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形。其中正确的是( )
A.①④ B.①② C.①②③ D.②③④
二、填空题
6.如图,中,,,,将绕点C顺时针旋转,得到,A、B的对应点分别为、,当时,则的长为 .
7.如图,在中,,且,,点是斜边上的一个动点,过点分别作于点,于点,连接,则线段的最小值为 .
8.如图,创新小组要测量公园内一棵树AB的高度,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为45°,已知测角仪的架高CE=1.2米,则这棵树的高度为 米.
9.如图,四边形ABCD是平行四边形,添加一个条件: ,可使它成为矩形.
10.木工师傅要做一张长方形的桌面.完成后,量得桌面的长为,宽为,对角线为130cm,则做出的这个桌面 .(填“合格”或“不合格”)
11.如图,在平行四边形中,延长到点E,使,连接、、请你添加一个条件,使四边形是矩形.
三、计算题
12.数形结合思想可以借助于数的精确性来阐明形的某些属性,或者借助形的几何直观来阐明数之间某种关系.
(1)2002年世界数学家大会(ICM2002)在北京召开,这届大会会标(如图1)的中央图案是经过艺术处理的“弦图”(如图2),它由4个全等的直角三角形拼成,请观察“弦图”直接写出满足的等量关系为______.
(2)某数学兴趣小组,采用数形结合思想解决了如下问题:
已知线段,点在线段上,,求的最小值.
他们解决问题的思路是:如图3,在线段的同侧构造了两个和,,令,利用勾股定理,得出,从而将问题转化成求“最小值”问题,再利用“将军饮马”模型,就完成了解答.请你写出解答过程;
(3)如图4,在中,,点分别为上的动点,且,求的最小值.
四、解答题
13.如图,在四边形中,,,,,点P从点D出发,以每秒1个单位长度的速度向点A运动,点Q从点B同时出发,以每秒2个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P运动时间为t秒.
(1)当点P运动停止时,______,线段的长为______;
(2)①用含t的式子填空:______,______,______;
② t为何值时,四边形为矩形,求出t的值;
(3)在运动的过程中,是否存在某一时刻t,使以P,D,C,Q为顶点的四边形为平行四边形?若存在,请求出t的值,若不存在,请说明理由.
五、综合题
14. ABCD中,过点D作DE⊥AB于点E,点F在CD上,DF=BE,连接:BF,AF。
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE-3,DF=5,求矩形BFDE的面积。
15.如图, ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,无需说明理由.
16.如图,在△ABC中,点O是AC边上一动点,过点O作DE,使DE∥BC,DE交∠ACB的角平分线于点D,交∠ACB的外角平分线于点E.
(1)求证:OD=OE;
(2)当点O运动到何处时,四边形CDAE是矩形 请证明你的结论.
答案解析部分
1.【答案】C
【知识点】矩形的判定
2.【答案】C
【知识点】矩形的判定
3.【答案】A
【知识点】矩形的判定与性质;旋转的性质
4.【答案】C
【知识点】垂线段最短及其应用;勾股定理;矩形的判定与性质
5.【答案】A
【知识点】平行线的性质;角平分线的性质;矩形的判定;直角三角形的性质
6.【答案】
【知识点】勾股定理;矩形的判定与性质;旋转的性质
7.【答案】
【知识点】勾股定理;矩形的判定与性质
8.【答案】11.2
【知识点】等腰三角形的判定与性质;矩形的判定与性质;线段的和、差、倍、分的简单计算
9.【答案】∠ABC=90°(或AC=BD等)
【知识点】矩形的判定
10.【答案】不合格
【知识点】勾股定理的逆定理;矩形的判定
11.【答案】(答案不唯一)
【知识点】矩形的判定
12.【答案】(1);
(2)的最小值为;
(3)的最小值为.
【知识点】勾股定理;矩形的判定与性质;轴对称的性质
13.【答案】(1);
(2)①;;;②
(3)
【知识点】平行四边形的性质;矩形的判定;一元一次方程的实际应用-几何问题
14.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形
∵DE⊥AB,∴∠DEB=90°,
∴四边形BFDE是矩形
(2)解:∵AB∥CD,
∴∠BAF=∠DFA,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠DFA=∠DAF,
∴AD=DF=5,
∵DE⊥AB,
∴∠AED=90°,由勾股定理得:DE= =4,
∴矩形BFDE的面积=DF×DE=5×4=20
【知识点】矩形的判定
15.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,∴OE=OF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(SAS).
(2)解:四边形EBFD是矩形;
理由如下:
∵OB=OD,OE=OF,∴四边形EBFD是平行四边形,∵BD=EF,∴四边形EBFD是矩形.
【知识点】全等三角形的判定与性质;平行四边形的性质;矩形的判定
16.【答案】(1)解:∵DE∥BC
∴∠ODC=∠DCB
又CD平分∠ACB
∴∠OCD=∠DCB
∴∠ODC=∠OCD
∴OD=OC
同理,OE=OC
∴OD=OE
(2)解:当点O运动到AC的中点时,四边形CDAE是矩形.
∵O为AC的中点
∴OA=OC
又OD=OE
∴四边形CDAE是平行四边形
又∵CD平分∠ACB,CE平分∠ACF
∴∠OCD+∠OCE=90°
即∠DCE=90°
∴四边形CDAE是矩形
【知识点】等式的基本性质;等腰三角形的性质;矩形的判定;角平分线的概念
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
