2.6.1菱形的性质 同步练习(含答案)
文档属性
| 名称 | 2.6.1菱形的性质 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 534.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.6.1菱形的性质
一、单选题
1.如图,菱形中,分别是的中点,若,则菱形的周长为( )
A.24 B.18 C.12 D.9
2.菱形具有而矩形不具有的性质是( )
A.两组对边分别平行 B.对角线相等
C.对角线互相垂直 D.两组对角分别相等
3.菱形ABCD的对角线AC,BD相交于点O,AC=10,BD=24,则菱形ABCD的周长为( )
A.52 B.48 C.40 D.20
4.如图,四边形为菱形,,两点的坐标分别是,,点,在坐标轴上,则菱形的周长等于( )
A.8 B.4 C.2 D.4
5.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
二、填空题
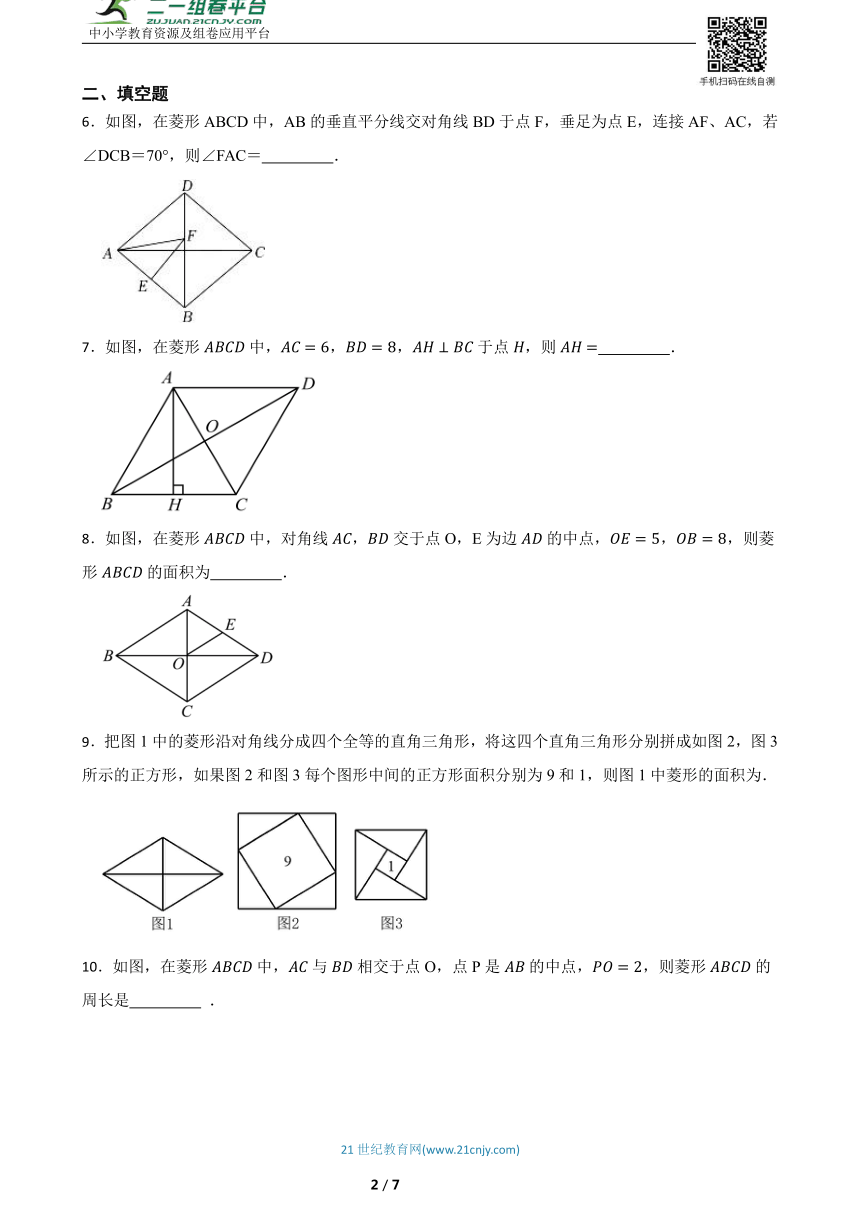
6.如图,在菱形ABCD中,AB的垂直平分线交对角线BD于点F,垂足为点E,连接AF、AC,若∠DCB=70°,则∠FAC= .
7.如图,在菱形中,,,于点,则 .
8.如图,在菱形中,对角线,交于点O,E为边的中点,,,则菱形的面积为 .
9.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,如果图2和图3每个图形中间的正方形面积分别为9和1,则图1中菱形的面积为.
10.如图,在菱形中,与相交于点O,点P是的中点,,则菱形的周长是 .
11.已知菱形中,对角线,,面积是 .
三、计算题
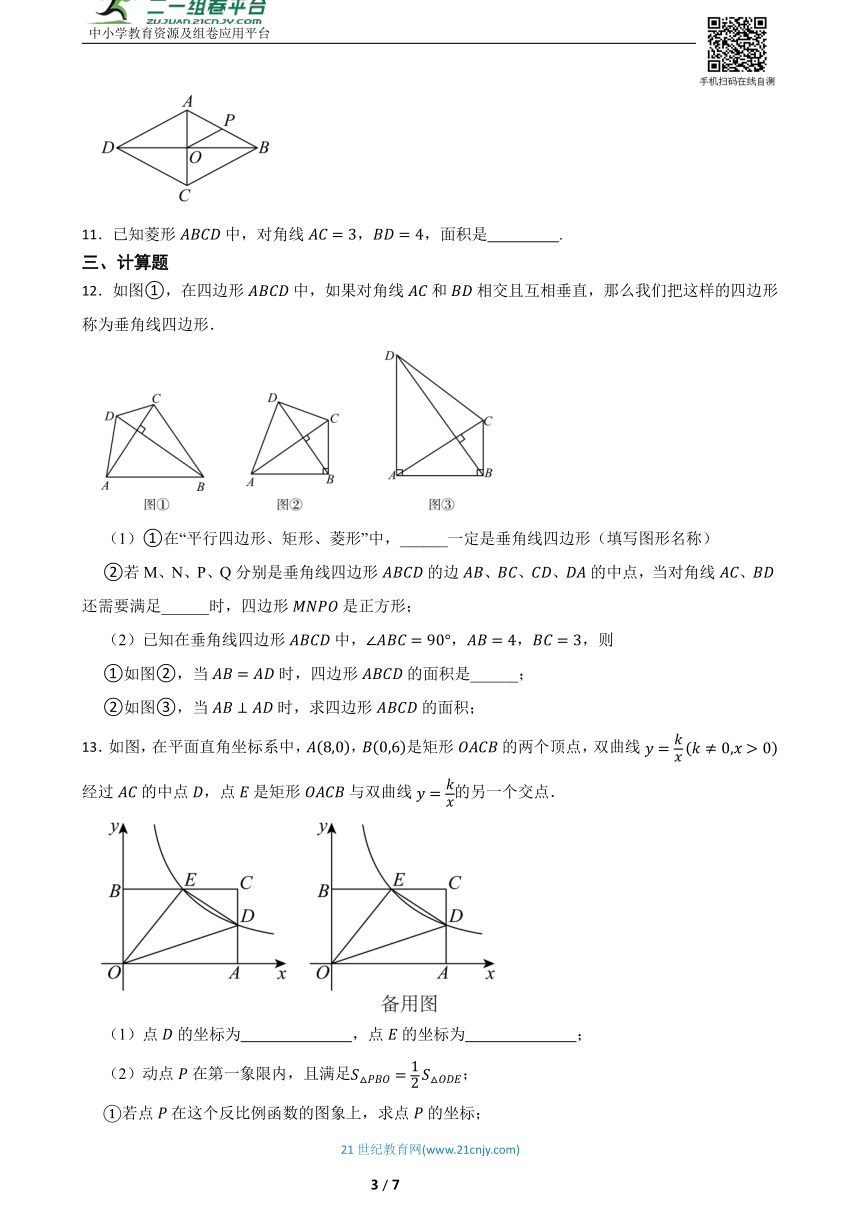
12.如图①,在四边形中,如果对角线和相交且互相垂直,那么我们把这样的四边形称为垂角线四边形.
(1)①在“平行四边形、矩形、菱形”中,______一定是垂角线四边形(填写图形名称)
②若M、N、P、Q分别是垂角线四边形的边、、、的中点,当对角线、还需要满足______时,四边形是正方形;
(2)已知在垂角线四边形中,,,,则
①如图②,当时,四边形的面积是______;
②如图③,当时,求四边形的面积;
13.如图,在平面直角坐标系中,,是矩形的两个顶点,双曲线经过的中点,点是矩形与双曲线的另一个交点.
(1)点的坐标为 ,点的坐标为 ;
(2)动点在第一象限内,且满足;
若点在这个反比例函数的图象上,求点的坐标;
若点是平面内一点,使得以为顶点的四边形是菱形,请你直接写出满足条件的所有点的坐标.
四、解答题
14.如图,四边形是菱形,于点H,求的长.
五、综合题
15.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
16.如图,某型号千斤顶的工作原理是利用四边形的不稳定性,图中的菱形是该型号千斤顶的示意图,保持菱形边长不变,可通过改变的长来调节的长.已知,的初始长为,如果要使的长达到,那么的长需要缩短多少.
17.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.
(1)求证:AE=BF;
(2)若点E恰好是AD的中点,AB=2,求BD的值.
答案解析部分
1.【答案】A
【知识点】菱形的性质;三角形的中位线定理
2.【答案】C
【知识点】菱形的性质;矩形的性质
3.【答案】A
【知识点】菱形的性质
4.【答案】A
【知识点】菱形的性质
5.【答案】A
【知识点】菱形的性质
6.【答案】20°
【知识点】线段垂直平分线的性质;菱形的性质
7.【答案】
【知识点】勾股定理;菱形的性质
8.【答案】96
【知识点】菱形的性质
9.【答案】8
【知识点】完全平方公式的几何背景;勾股定理;菱形的性质
10.【答案】
【知识点】菱形的性质;直角三角形斜边上的中线
11.【答案】6
【知识点】菱形的性质
12.【答案】(1)①菱形;②
(2)①12;②
【知识点】勾股定理;菱形的性质;三角形全等的判定-SAS;三角形的中位线定理
13.【答案】(1),;
(2);或或或.
【知识点】勾股定理;菱形的性质;矩形的性质
14.【答案】
【知识点】勾股定理;菱形的性质
15.【答案】(1)解:∵ABCD是菱形,
∴AC⊥BD,
∴直角△OCD中,OC= (cm)
(2)解:∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形,
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形,
∵OB=0D,
∴S矩形OBEC=OB OC=4×3=12(cm2)
【知识点】菱形的性质;矩形的判定与性质
16.【答案】的长需要缩短
【知识点】勾股定理;菱形的性质
17.【答案】(1)证明:四边形ABCD是菱形
∴AB=BC,AD∥BC
∴∠A=∠CBF
∵BE⊥AD、CF⊥AB
∴∠AEB=∠BFC=90°
∴△AEB≌△BFC(AAS)
∴AE=BF
(2)解:∵E是AD中点,且BE⊥AD
∴直线BE为AD的垂直平分线
∴BD=AB=2
【知识点】线段垂直平分线的性质;菱形的性质
21世纪教育网(www.21cnjy.com)
2 / 7
2.6.1菱形的性质
一、单选题
1.如图,菱形中,分别是的中点,若,则菱形的周长为( )
A.24 B.18 C.12 D.9
2.菱形具有而矩形不具有的性质是( )
A.两组对边分别平行 B.对角线相等
C.对角线互相垂直 D.两组对角分别相等
3.菱形ABCD的对角线AC,BD相交于点O,AC=10,BD=24,则菱形ABCD的周长为( )
A.52 B.48 C.40 D.20
4.如图,四边形为菱形,,两点的坐标分别是,,点,在坐标轴上,则菱形的周长等于( )
A.8 B.4 C.2 D.4
5.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
二、填空题
6.如图,在菱形ABCD中,AB的垂直平分线交对角线BD于点F,垂足为点E,连接AF、AC,若∠DCB=70°,则∠FAC= .
7.如图,在菱形中,,,于点,则 .
8.如图,在菱形中,对角线,交于点O,E为边的中点,,,则菱形的面积为 .
9.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,如果图2和图3每个图形中间的正方形面积分别为9和1,则图1中菱形的面积为.
10.如图,在菱形中,与相交于点O,点P是的中点,,则菱形的周长是 .
11.已知菱形中,对角线,,面积是 .
三、计算题
12.如图①,在四边形中,如果对角线和相交且互相垂直,那么我们把这样的四边形称为垂角线四边形.
(1)①在“平行四边形、矩形、菱形”中,______一定是垂角线四边形(填写图形名称)
②若M、N、P、Q分别是垂角线四边形的边、、、的中点,当对角线、还需要满足______时,四边形是正方形;
(2)已知在垂角线四边形中,,,,则
①如图②,当时,四边形的面积是______;
②如图③,当时,求四边形的面积;
13.如图,在平面直角坐标系中,,是矩形的两个顶点,双曲线经过的中点,点是矩形与双曲线的另一个交点.
(1)点的坐标为 ,点的坐标为 ;
(2)动点在第一象限内,且满足;
若点在这个反比例函数的图象上,求点的坐标;
若点是平面内一点,使得以为顶点的四边形是菱形,请你直接写出满足条件的所有点的坐标.
四、解答题
14.如图,四边形是菱形,于点H,求的长.
五、综合题
15.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
16.如图,某型号千斤顶的工作原理是利用四边形的不稳定性,图中的菱形是该型号千斤顶的示意图,保持菱形边长不变,可通过改变的长来调节的长.已知,的初始长为,如果要使的长达到,那么的长需要缩短多少.
17.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.
(1)求证:AE=BF;
(2)若点E恰好是AD的中点,AB=2,求BD的值.
答案解析部分
1.【答案】A
【知识点】菱形的性质;三角形的中位线定理
2.【答案】C
【知识点】菱形的性质;矩形的性质
3.【答案】A
【知识点】菱形的性质
4.【答案】A
【知识点】菱形的性质
5.【答案】A
【知识点】菱形的性质
6.【答案】20°
【知识点】线段垂直平分线的性质;菱形的性质
7.【答案】
【知识点】勾股定理;菱形的性质
8.【答案】96
【知识点】菱形的性质
9.【答案】8
【知识点】完全平方公式的几何背景;勾股定理;菱形的性质
10.【答案】
【知识点】菱形的性质;直角三角形斜边上的中线
11.【答案】6
【知识点】菱形的性质
12.【答案】(1)①菱形;②
(2)①12;②
【知识点】勾股定理;菱形的性质;三角形全等的判定-SAS;三角形的中位线定理
13.【答案】(1),;
(2);或或或.
【知识点】勾股定理;菱形的性质;矩形的性质
14.【答案】
【知识点】勾股定理;菱形的性质
15.【答案】(1)解:∵ABCD是菱形,
∴AC⊥BD,
∴直角△OCD中,OC= (cm)
(2)解:∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形,
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形,
∵OB=0D,
∴S矩形OBEC=OB OC=4×3=12(cm2)
【知识点】菱形的性质;矩形的判定与性质
16.【答案】的长需要缩短
【知识点】勾股定理;菱形的性质
17.【答案】(1)证明:四边形ABCD是菱形
∴AB=BC,AD∥BC
∴∠A=∠CBF
∵BE⊥AD、CF⊥AB
∴∠AEB=∠BFC=90°
∴△AEB≌△BFC(AAS)
∴AE=BF
(2)解:∵E是AD中点,且BE⊥AD
∴直线BE为AD的垂直平分线
∴BD=AB=2
【知识点】线段垂直平分线的性质;菱形的性质
21世纪教育网(www.21cnjy.com)
2 / 7
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
