第二章 四边形 章末练习【培优】(含答案)
文档属性
| 名称 | 第二章 四边形 章末练习【培优】(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 692.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二章 多边形【培优】
一、单选题
1.四条边相等的图形可能是( ).
A.三角形 B.梯形 C.平行四边形 D.六边形
2.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD的中点,若BC=2,则EF的长度为( )
A. B.1 C. D.
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.下列汽车标志中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
6.已知:正方形的边长为8,点、分别在、上,,与相交于点,点为的中点,连接,则的长为( )
A.3 B.4 C. D.5
7.在平行四边形的复习课上,小明绘制了如下知识框架图,箭头处添加条件错误的是( )
A.①:一组邻边互相垂直 B.②:对角线相等
C.③:对角线互相垂直 D.④:有一个角是直角
8.用折纸、剪切的方法得到一个菱形,最少要剪( )刀(设一条线段剪一刀)
A.1 B.2 C.3 D.4
9.如图,某花木场有一块如四边形形状的空地,其中,其各边中点分别是E、F、G、H,测得对角线,现想利用篱笆围成四边形场地,则需篱笆的总长度是( )
A. B. C. D.
10.如图,正方形边长为1,点在边上(不与重合),将沿直线折叠,点落在点处,连接,将绕点顺时针旋转得到,连接.给出下列四个结论:①;②;③点是直线上动点,则的最小值为;④当时,的面积为.其中正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
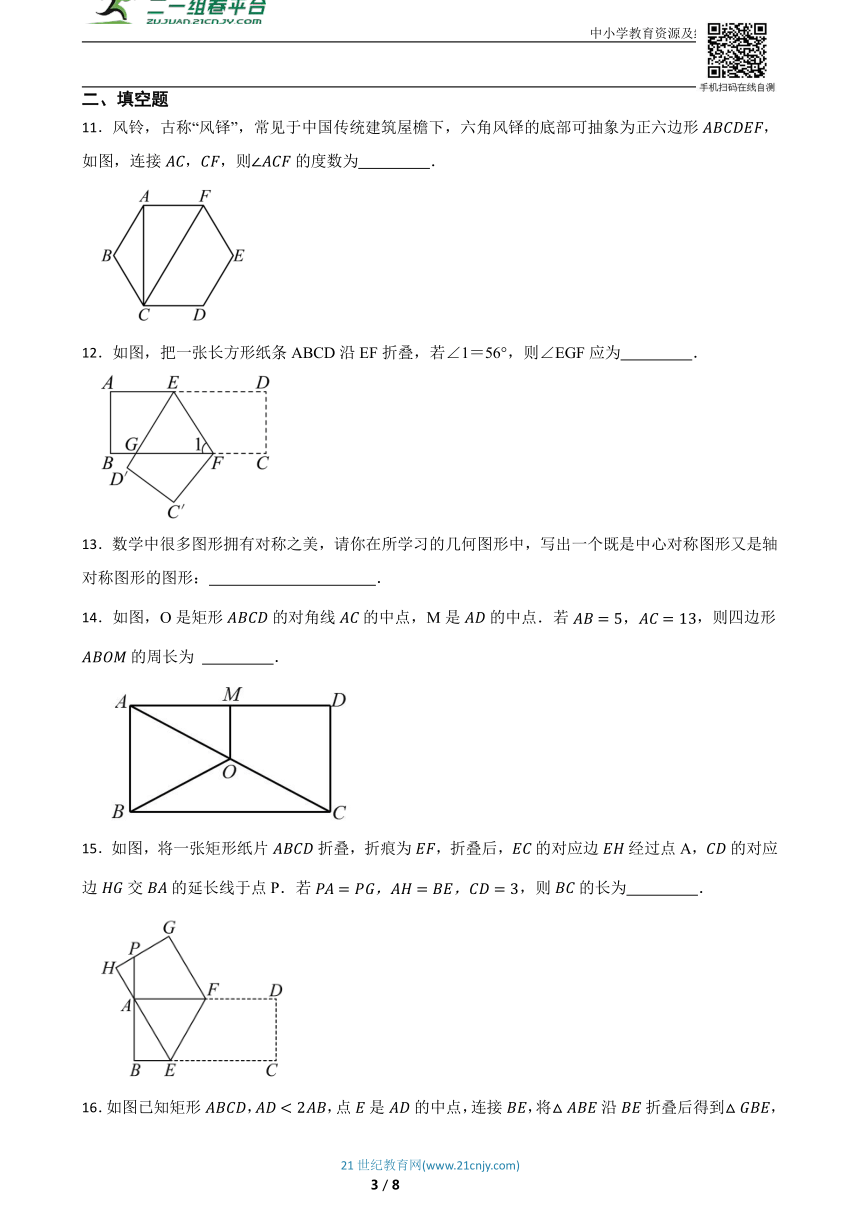
11.风铃,古称“风铎”,常见于中国传统建筑屋檐下,六角风铎的底部可抽象为正六边形,如图,连接,,则的度数为 .
12.如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为 .
13.数学中很多图形拥有对称之美,请你在所学习的几何图形中,写出一个既是中心对称图形又是轴对称图形的图形: .
14.如图,O是矩形的对角线的中点,M是的中点.若,则四边形的周长为 .
15.如图,将一张矩形纸片折叠,折痕为,折叠后,的对应边经过点A,的对应边交的延长线于点P.若,则的长为 .
16.如图已知矩形,,点是的中点,连接,将沿折叠后得到,延长交于点,连接.若点是的中点,,求的长是 .
三、计算题
17.若边形的内角和为,求的值.
18.如图,四边形是边长为的正方形,是上一点,,将绕着点顺时针旋转到与重合,求的长.
19.【问题情景】如图正方形是绿地公园的一块空地,其边长为60米.公园设计部门为了给儿童提供更舒适更安全的活动场地,准备将空地中的四边形部分作为儿童活动区,并用围栏围挡起来,只留三个出入口,即点、点、点,而且根据实际需要,要使得度,并将儿童活动区(即四边形)划分为和两种不同的游戏场地,儿童活动区之外的部分种植花草.
(1)【模型感知】请直接写出线段之间的数量关系;
(2)【模型应用】如图②,若m,请你计算儿童活动区的面积;
(3)【模型拓展】如图③,连接,若与线段分别交于点、点,则和仍满足(1)中的数量关系吗?若不满足,请写出新的数量关系并说明理由.
四、解答题
20.已知正多边形的一个内角是它的外角的4倍,求这个正多边形的边数.
21.阅读明明和芳芳的对话,解答下列问题.
(1)明明通过计算,发现少加了一个锐角,则这个“少加的锐角”的度数是__________.
(2)明明求的是几边形的内角和?
(3)这个多边形对角线的总条数是__________.
22. 如图,菱形中,对角线、相交于点O,过点C作,过点D作,与相交于点E.
(1)求证:四边形是矩形.
(2)若,,求四边形的周长.
23.如图,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)在我们学过:①平行四边形、②矩形、③菱形、④正方形,能称为垂美四边形的是 ;(只填序号)
(2)如图,垂美四边形的对角线交于点,求的长度.
答案解析部分
1.【答案】C
【知识点】平行四边形的性质
2.【答案】B
【知识点】含30°角的直角三角形;三角形的中位线定理;直角三角形斜边上的中线
3.【答案】A
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】D
【知识点】轴对称图形;中心对称及中心对称图形
5.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
6.【答案】D
【知识点】勾股定理;正方形的性质;三角形全等的判定-SAS
7.【答案】B
【知识点】菱形的判定;矩形的判定;正方形的判定
8.【答案】A
【知识点】菱形的判定
9.【答案】C
【知识点】等腰三角形的判定;平行四边形的判定与性质;三角形全等的判定-SAS;三角形的中位线定理
10.【答案】C
【知识点】正方形的性质;轴对称的应用-最短距离问题;翻折变换(折叠问题);旋转的性质;三角形全等的判定-SAS
11.【答案】
【知识点】三角形内角和定理;等腰三角形的性质;多边形内角与外角
12.【答案】68°
【知识点】矩形的性质
13.【答案】圆(答案不唯一)
【知识点】轴对称图形;中心对称及中心对称图形
14.【答案】20
【知识点】勾股定理;矩形的性质;三角形的中位线定理;直角三角形斜边上的中线
15.【答案】
【知识点】直角三角形全等的判定-HL;勾股定理;矩形的性质
16.【答案】
【知识点】直角三角形全等的判定-HL;勾股定理;矩形的性质
17.【答案】13
【知识点】多边形内角与外角
18.【答案】
【知识点】勾股定理;正方形的性质;旋转的性质
19.【答案】(1)
(2)
(3)
【知识点】三角形全等及其性质;勾股定理;正方形的性质;旋转的性质
20.【答案】设这个正多边形的边数n边形,由题意得:
,
解得:,
答:这个正多边形的边数是10.
【知识点】多边形内角与外角;一元一次方程的实际应用-几何问题
21.【答案】(1)20
(2)明明求的是八边形的内角和
(3)20
【知识点】多边形的对角线;多边形内角与外角
22.【答案】(1)证明:,,
四边形是平行四边形,
四边形是菱形,
,
,
四边形是矩形.
(2)解:四边形是菱形,AB=10,AC=12,
,,
∵∠COD=90°,
,
四边形是矩形,
四边形的周长是2(OC+OD)=2×(6+8)=28.
【知识点】勾股定理;菱形的性质;矩形的性质;矩形的判定
23.【答案】(1)③④
(2)
【知识点】勾股定理;菱形的性质;矩形的性质;正方形的性质
21世纪教育网(www.21cnjy.com)
1 / 8
第二章 多边形【培优】
一、单选题
1.四条边相等的图形可能是( ).
A.三角形 B.梯形 C.平行四边形 D.六边形
2.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD的中点,若BC=2,则EF的长度为( )
A. B.1 C. D.
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.下列汽车标志中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
5.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
6.已知:正方形的边长为8,点、分别在、上,,与相交于点,点为的中点,连接,则的长为( )
A.3 B.4 C. D.5
7.在平行四边形的复习课上,小明绘制了如下知识框架图,箭头处添加条件错误的是( )
A.①:一组邻边互相垂直 B.②:对角线相等
C.③:对角线互相垂直 D.④:有一个角是直角
8.用折纸、剪切的方法得到一个菱形,最少要剪( )刀(设一条线段剪一刀)
A.1 B.2 C.3 D.4
9.如图,某花木场有一块如四边形形状的空地,其中,其各边中点分别是E、F、G、H,测得对角线,现想利用篱笆围成四边形场地,则需篱笆的总长度是( )
A. B. C. D.
10.如图,正方形边长为1,点在边上(不与重合),将沿直线折叠,点落在点处,连接,将绕点顺时针旋转得到,连接.给出下列四个结论:①;②;③点是直线上动点,则的最小值为;④当时,的面积为.其中正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.风铃,古称“风铎”,常见于中国传统建筑屋檐下,六角风铎的底部可抽象为正六边形,如图,连接,,则的度数为 .
12.如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为 .
13.数学中很多图形拥有对称之美,请你在所学习的几何图形中,写出一个既是中心对称图形又是轴对称图形的图形: .
14.如图,O是矩形的对角线的中点,M是的中点.若,则四边形的周长为 .
15.如图,将一张矩形纸片折叠,折痕为,折叠后,的对应边经过点A,的对应边交的延长线于点P.若,则的长为 .
16.如图已知矩形,,点是的中点,连接,将沿折叠后得到,延长交于点,连接.若点是的中点,,求的长是 .
三、计算题
17.若边形的内角和为,求的值.
18.如图,四边形是边长为的正方形,是上一点,,将绕着点顺时针旋转到与重合,求的长.
19.【问题情景】如图正方形是绿地公园的一块空地,其边长为60米.公园设计部门为了给儿童提供更舒适更安全的活动场地,准备将空地中的四边形部分作为儿童活动区,并用围栏围挡起来,只留三个出入口,即点、点、点,而且根据实际需要,要使得度,并将儿童活动区(即四边形)划分为和两种不同的游戏场地,儿童活动区之外的部分种植花草.
(1)【模型感知】请直接写出线段之间的数量关系;
(2)【模型应用】如图②,若m,请你计算儿童活动区的面积;
(3)【模型拓展】如图③,连接,若与线段分别交于点、点,则和仍满足(1)中的数量关系吗?若不满足,请写出新的数量关系并说明理由.
四、解答题
20.已知正多边形的一个内角是它的外角的4倍,求这个正多边形的边数.
21.阅读明明和芳芳的对话,解答下列问题.
(1)明明通过计算,发现少加了一个锐角,则这个“少加的锐角”的度数是__________.
(2)明明求的是几边形的内角和?
(3)这个多边形对角线的总条数是__________.
22. 如图,菱形中,对角线、相交于点O,过点C作,过点D作,与相交于点E.
(1)求证:四边形是矩形.
(2)若,,求四边形的周长.
23.如图,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)在我们学过:①平行四边形、②矩形、③菱形、④正方形,能称为垂美四边形的是 ;(只填序号)
(2)如图,垂美四边形的对角线交于点,求的长度.
答案解析部分
1.【答案】C
【知识点】平行四边形的性质
2.【答案】B
【知识点】含30°角的直角三角形;三角形的中位线定理;直角三角形斜边上的中线
3.【答案】A
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】D
【知识点】轴对称图形;中心对称及中心对称图形
5.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
6.【答案】D
【知识点】勾股定理;正方形的性质;三角形全等的判定-SAS
7.【答案】B
【知识点】菱形的判定;矩形的判定;正方形的判定
8.【答案】A
【知识点】菱形的判定
9.【答案】C
【知识点】等腰三角形的判定;平行四边形的判定与性质;三角形全等的判定-SAS;三角形的中位线定理
10.【答案】C
【知识点】正方形的性质;轴对称的应用-最短距离问题;翻折变换(折叠问题);旋转的性质;三角形全等的判定-SAS
11.【答案】
【知识点】三角形内角和定理;等腰三角形的性质;多边形内角与外角
12.【答案】68°
【知识点】矩形的性质
13.【答案】圆(答案不唯一)
【知识点】轴对称图形;中心对称及中心对称图形
14.【答案】20
【知识点】勾股定理;矩形的性质;三角形的中位线定理;直角三角形斜边上的中线
15.【答案】
【知识点】直角三角形全等的判定-HL;勾股定理;矩形的性质
16.【答案】
【知识点】直角三角形全等的判定-HL;勾股定理;矩形的性质
17.【答案】13
【知识点】多边形内角与外角
18.【答案】
【知识点】勾股定理;正方形的性质;旋转的性质
19.【答案】(1)
(2)
(3)
【知识点】三角形全等及其性质;勾股定理;正方形的性质;旋转的性质
20.【答案】设这个正多边形的边数n边形,由题意得:
,
解得:,
答:这个正多边形的边数是10.
【知识点】多边形内角与外角;一元一次方程的实际应用-几何问题
21.【答案】(1)20
(2)明明求的是八边形的内角和
(3)20
【知识点】多边形的对角线;多边形内角与外角
22.【答案】(1)证明:,,
四边形是平行四边形,
四边形是菱形,
,
,
四边形是矩形.
(2)解:四边形是菱形,AB=10,AC=12,
,,
∵∠COD=90°,
,
四边形是矩形,
四边形的周长是2(OC+OD)=2×(6+8)=28.
【知识点】勾股定理;菱形的性质;矩形的性质;矩形的判定
23.【答案】(1)③④
(2)
【知识点】勾股定理;菱形的性质;矩形的性质;正方形的性质
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
