4.5一次函数的应用 同步练习(含答案)
文档属性
| 名称 | 4.5一次函数的应用 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 298.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.5一次函数的应用
一、单选题
1.把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y关于x的函数关系式为( )
A.y=24-x B.y=8x-24 C.y=8x D.y=8x+24
2.一种弹簧秤最大能称10kg的物体,不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm.在弹性限度内,挂重后弹簧的长度y(cm)关于所挂物体的质量x(kg)的函数表达式为( )
A.y=12-0.5x B.y=12+0.5x C.y=10+0.5x D.y=0.5x
3.汽车离开甲站10千米后,以60千米/时的速度匀速前进了小时,则汽车离开甲站所走的路程(千米)与时间(小时)之间的关系式是( )
A. B. C. D.
4.早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
①打电话时,小刚和妈妈的距离为1250米;
②打完电话后,经过23分钟小刚到达学校;
③小刚和妈妈相遇后,妈妈回家的速度为150米/分;
④小刚家与学校的距离为2550米.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,元旦期间,某移动公司推出两种不同的收费标准:A种方式是月租20元,B种方式是月租0元,一个月本地网内打出时间t(分)与打出电话费s(元)的函数关系图象,当打出200分钟时,这两种方式的电话费相差( )
A.15元 B.20元 C.25元 D.30元
二、填空题
6.已知等腰三角形的周长为24,底边y关于腰长x的函数解析式是 .
7. 已知,请用表示为 .
8.某衬衣定价为100元时,每月可卖出2000件,受成本影响,该衬衣需涨价,已知价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与衬衣价格x(元)之间的关系式为 .
9.和谐号动车刹车后作匀减速运动,速度与刹车时间与之间满足关系式.动车在匀变速直线运动中,从开始刹车到准确停到站台,需要 .
10.一根蜡烛燃烧过程中,剩余蜡烛长y(厘米)和燃烧时间x(小时)的关系如图所示,则这根蜡烛燃烧4小时,剩余蜡烛长为 厘米.
11.如表反映的是高速路上匀速行驶的汽车在行驶过程中时x(时)与邮箱的余油量y (升)之间的关系,写出y与x的函数表达式
行驶时间x(时) 0 1 2 3 …
余油量y(升) 60 50 40 30 …
三、计算题
12.1号探测气球从海拔5m出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间t(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多少时间?位于什么高度?
四、解答题
13.已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7. 2厘米,求这个一次函数的关系式.
五、作图题
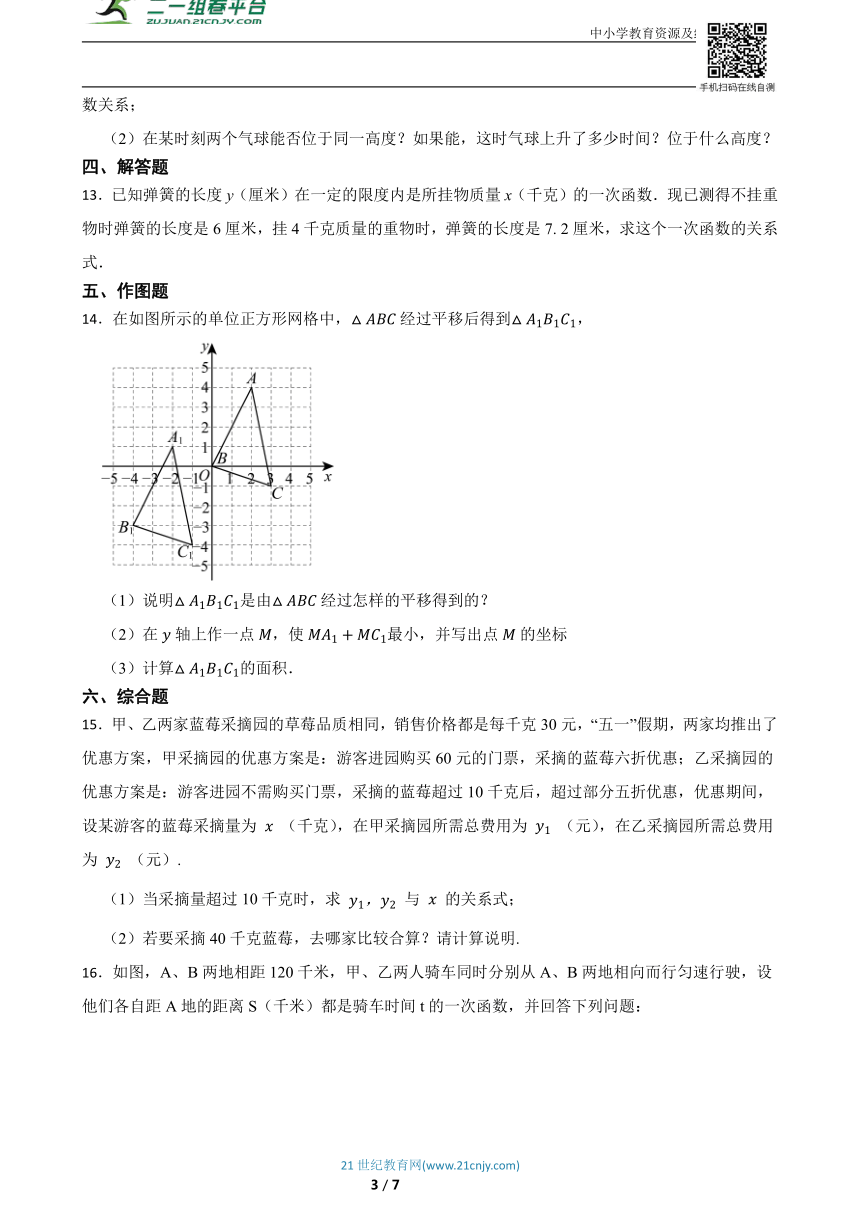
14.在如图所示的单位正方形网格中,经过平移后得到,
(1)说明是由经过怎样的平移得到的?
(2)在轴上作一点,使最小,并写出点的坐标
(3)计算的面积.
六、综合题
15.甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为 (千克),在甲采摘园所需总费用为 (元),在乙采摘园所需总费用为 (元).
(1)当采摘量超过10千克时,求 与 的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
16.如图,A、B两地相距120千米,甲、乙两人骑车同时分别从A、B两地相向而行匀速行驶,设他们各自距A地的距离S(千米)都是骑车时间t的一次函数,并回答下列问题:
(1)甲的速度为 千米/小时,乙的速度为 千米/小时;
(2)求运动过程中的函数解析式.
17.据测定,海底扩张的速度是很缓慢的,在太平洋海底,某海沟的某处宽度为100米,某两侧的地壳向扩张的速度是每年6米,假设海沟扩张速度恒定,扩张时间为x年,海沟的宽度为y米.
(1)写出海沟扩张时间x年与海沟的宽度y之间的表达式;
(2)你能计算以下当海沟宽度y扩张到400米时需要多少年吗?
答案解析部分
1.【答案】D
【知识点】列一次函数关系式
2.【答案】B
【知识点】列一次函数关系式
3.【答案】A
【知识点】列一次函数关系式
4.【答案】C
【知识点】一次函数的实际应用
5.【答案】B
【知识点】一次函数的实际应用
6.【答案】y=24-2x(6<x<12)
【知识点】等腰三角形的性质;列一次函数关系式
7.【答案】
【知识点】列一次函数关系式
8.【答案】y=﹣5x+2500
【知识点】列一次函数关系式
9.【答案】4
【知识点】一次函数的实际应用
10.【答案】10
【知识点】一次函数的图象;一次函数的实际应用
11.【答案】y=60-10x(0≤x≤6)
【知识点】列一次函数关系式
12.【答案】(1)解:根据题意得:1号探测气球所在位置的海拔:y1=t+5,2号探测气球所在位置的海拔:y2=0.5t+15;
(2)解:两个气球能位于同一高度,
根据题意得:t+5=0.5t+15,
解得:t=20,有t+5=25.
答:此时,气球上升了20分钟,都位于海拔25米的高度.
【知识点】一次函数的实际应用;列一次函数关系式
13.【答案】设所求函数的关系式是y=kx+b,
根据题意,得
解这个方程组,得
所以所求函数的关系式是y=0.3x+6
【知识点】列一次函数关系式
14.【答案】(1)先向下平移个单位,再向左平移个单位
(2)
(3)
【知识点】两点之间线段最短;坐标与图形变化﹣平移;列一次函数关系式
15.【答案】(1)解:根据题意得,
y1=60+30×0.6x=60+18x;
y2=10×30+30×0.5(x-10)=150+15x
(2)解:当x=40时,
y1=60+18×40=780,
y2=150+15×40=750,
因为y1>y2,
所以要采摘40千克蓝莓,去乙家比较合算.
【知识点】一次函数的实际应用
16.【答案】(1)15;25
(2)设直线的解析式为
解得:
函数解析式为
【知识点】一次函数的实际应用
17.【答案】(1)解:根据题意得:海沟增加的宽度为6x米,
∴海沟扩张时间x年与海沟的宽度y之间的表达式为:y=6x+100
(2)解:当y=400时,6x+100=400,
解得:x=50,
答:当海沟宽度y扩张到400米时需要50年
【知识点】待定系数法求一次函数解析式;列一次函数关系式
21世纪教育网(www.21cnjy.com)
1 / 7
4.5一次函数的应用
一、单选题
1.把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y关于x的函数关系式为( )
A.y=24-x B.y=8x-24 C.y=8x D.y=8x+24
2.一种弹簧秤最大能称10kg的物体,不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm.在弹性限度内,挂重后弹簧的长度y(cm)关于所挂物体的质量x(kg)的函数表达式为( )
A.y=12-0.5x B.y=12+0.5x C.y=10+0.5x D.y=0.5x
3.汽车离开甲站10千米后,以60千米/时的速度匀速前进了小时,则汽车离开甲站所走的路程(千米)与时间(小时)之间的关系式是( )
A. B. C. D.
4.早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
①打电话时,小刚和妈妈的距离为1250米;
②打完电话后,经过23分钟小刚到达学校;
③小刚和妈妈相遇后,妈妈回家的速度为150米/分;
④小刚家与学校的距离为2550米.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,元旦期间,某移动公司推出两种不同的收费标准:A种方式是月租20元,B种方式是月租0元,一个月本地网内打出时间t(分)与打出电话费s(元)的函数关系图象,当打出200分钟时,这两种方式的电话费相差( )
A.15元 B.20元 C.25元 D.30元
二、填空题
6.已知等腰三角形的周长为24,底边y关于腰长x的函数解析式是 .
7. 已知,请用表示为 .
8.某衬衣定价为100元时,每月可卖出2000件,受成本影响,该衬衣需涨价,已知价格每上涨10元,销售量便减少50件.那么,每月售出衬衣的总件数y(件)与衬衣价格x(元)之间的关系式为 .
9.和谐号动车刹车后作匀减速运动,速度与刹车时间与之间满足关系式.动车在匀变速直线运动中,从开始刹车到准确停到站台,需要 .
10.一根蜡烛燃烧过程中,剩余蜡烛长y(厘米)和燃烧时间x(小时)的关系如图所示,则这根蜡烛燃烧4小时,剩余蜡烛长为 厘米.
11.如表反映的是高速路上匀速行驶的汽车在行驶过程中时x(时)与邮箱的余油量y (升)之间的关系,写出y与x的函数表达式
行驶时间x(时) 0 1 2 3 …
余油量y(升) 60 50 40 30 …
三、计算题
12.1号探测气球从海拔5m出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都上升了1小时.
(1)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间t(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多少时间?位于什么高度?
四、解答题
13.已知弹簧的长度y(厘米)在一定的限度内是所挂物质量x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7. 2厘米,求这个一次函数的关系式.
五、作图题
14.在如图所示的单位正方形网格中,经过平移后得到,
(1)说明是由经过怎样的平移得到的?
(2)在轴上作一点,使最小,并写出点的坐标
(3)计算的面积.
六、综合题
15.甲、乙两家蓝莓采摘园的草莓品质相同,销售价格都是每千克30元,“五一”假期,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园购买60元的门票,采摘的蓝莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的蓝莓超过10千克后,超过部分五折优惠,优惠期间,设某游客的蓝莓采摘量为 (千克),在甲采摘园所需总费用为 (元),在乙采摘园所需总费用为 (元).
(1)当采摘量超过10千克时,求 与 的关系式;
(2)若要采摘40千克蓝莓,去哪家比较合算?请计算说明.
16.如图,A、B两地相距120千米,甲、乙两人骑车同时分别从A、B两地相向而行匀速行驶,设他们各自距A地的距离S(千米)都是骑车时间t的一次函数,并回答下列问题:
(1)甲的速度为 千米/小时,乙的速度为 千米/小时;
(2)求运动过程中的函数解析式.
17.据测定,海底扩张的速度是很缓慢的,在太平洋海底,某海沟的某处宽度为100米,某两侧的地壳向扩张的速度是每年6米,假设海沟扩张速度恒定,扩张时间为x年,海沟的宽度为y米.
(1)写出海沟扩张时间x年与海沟的宽度y之间的表达式;
(2)你能计算以下当海沟宽度y扩张到400米时需要多少年吗?
答案解析部分
1.【答案】D
【知识点】列一次函数关系式
2.【答案】B
【知识点】列一次函数关系式
3.【答案】A
【知识点】列一次函数关系式
4.【答案】C
【知识点】一次函数的实际应用
5.【答案】B
【知识点】一次函数的实际应用
6.【答案】y=24-2x(6<x<12)
【知识点】等腰三角形的性质;列一次函数关系式
7.【答案】
【知识点】列一次函数关系式
8.【答案】y=﹣5x+2500
【知识点】列一次函数关系式
9.【答案】4
【知识点】一次函数的实际应用
10.【答案】10
【知识点】一次函数的图象;一次函数的实际应用
11.【答案】y=60-10x(0≤x≤6)
【知识点】列一次函数关系式
12.【答案】(1)解:根据题意得:1号探测气球所在位置的海拔:y1=t+5,2号探测气球所在位置的海拔:y2=0.5t+15;
(2)解:两个气球能位于同一高度,
根据题意得:t+5=0.5t+15,
解得:t=20,有t+5=25.
答:此时,气球上升了20分钟,都位于海拔25米的高度.
【知识点】一次函数的实际应用;列一次函数关系式
13.【答案】设所求函数的关系式是y=kx+b,
根据题意,得
解这个方程组,得
所以所求函数的关系式是y=0.3x+6
【知识点】列一次函数关系式
14.【答案】(1)先向下平移个单位,再向左平移个单位
(2)
(3)
【知识点】两点之间线段最短;坐标与图形变化﹣平移;列一次函数关系式
15.【答案】(1)解:根据题意得,
y1=60+30×0.6x=60+18x;
y2=10×30+30×0.5(x-10)=150+15x
(2)解:当x=40时,
y1=60+18×40=780,
y2=150+15×40=750,
因为y1>y2,
所以要采摘40千克蓝莓,去乙家比较合算.
【知识点】一次函数的实际应用
16.【答案】(1)15;25
(2)设直线的解析式为
解得:
函数解析式为
【知识点】一次函数的实际应用
17.【答案】(1)解:根据题意得:海沟增加的宽度为6x米,
∴海沟扩张时间x年与海沟的宽度y之间的表达式为:y=6x+100
(2)解:当y=400时,6x+100=400,
解得:x=50,
答:当海沟宽度y扩张到400米时需要50年
【知识点】待定系数法求一次函数解析式;列一次函数关系式
21世纪教育网(www.21cnjy.com)
1 / 7
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
