第四章 一次函数 章末练习【培优】(含答案)
文档属性
| 名称 | 第四章 一次函数 章末练习【培优】(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 473.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第四章 一次函数【培优】
一、单选题
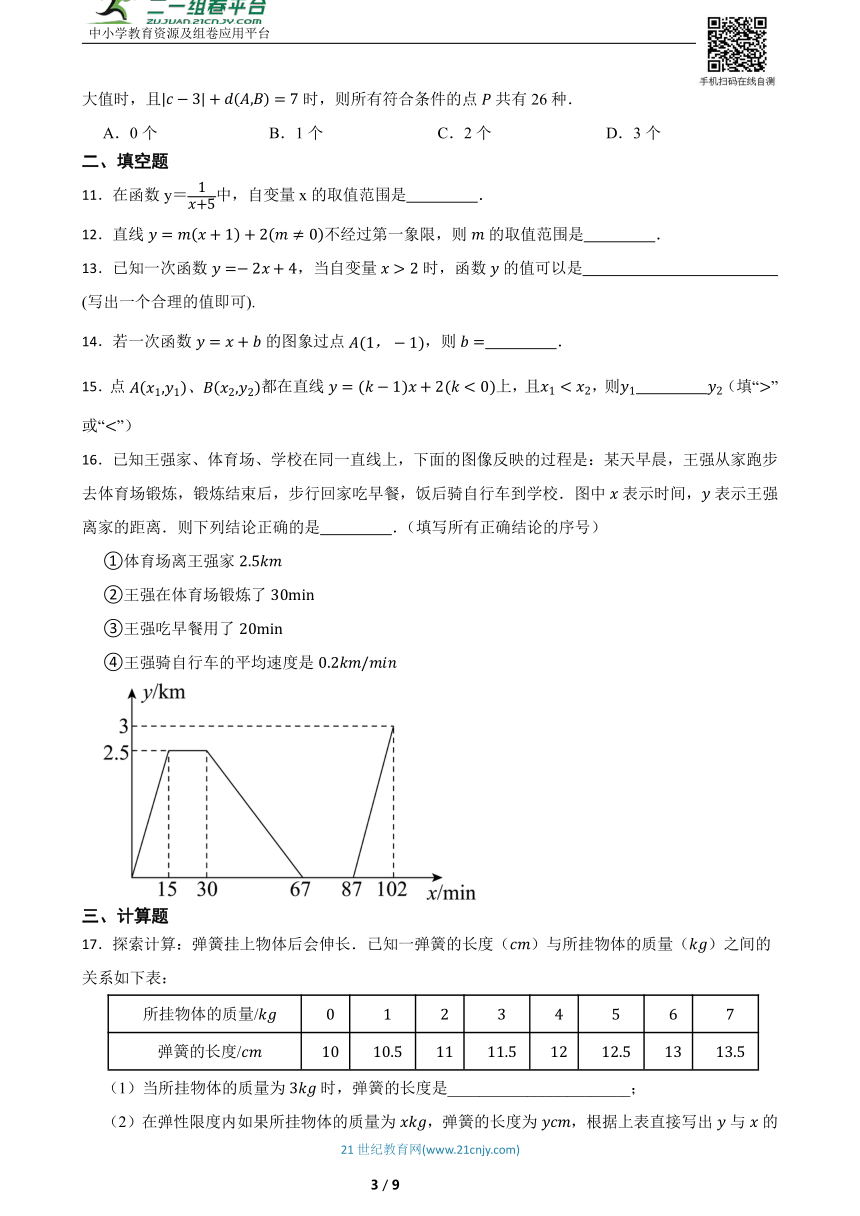
1.弹簧挂上物体后会伸长,测得弹簧的长度()与所挂的物体的质量()之间有下面的关系:
下列说法不正确的是( ).
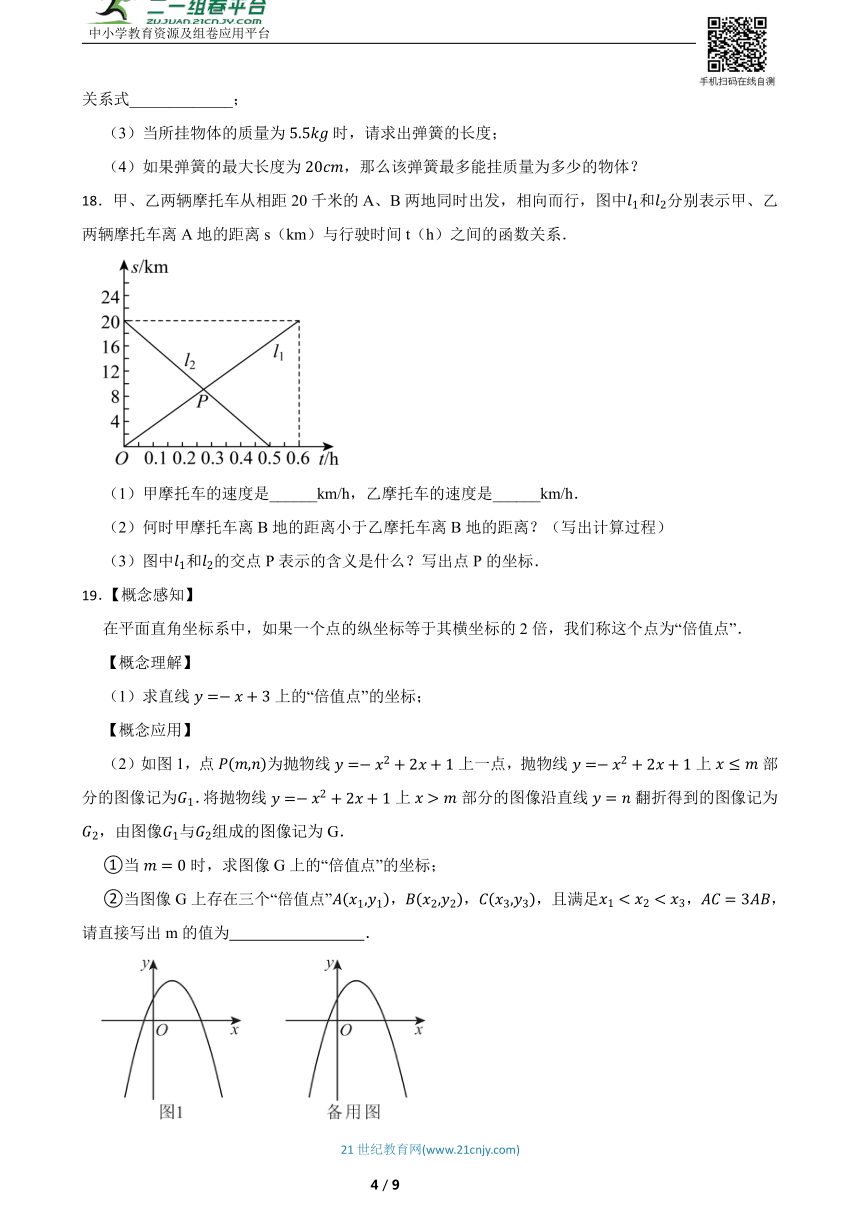
A.与都是变量,且是自变量,是因变量
B.所挂物体质量为时,弹簧长度为
C.物体质量每增加,弹簧长度增加
D.弹簧不挂重物时的长度为
2.下列函数关系式:①,②,③,④,⑤,其中是一次函数的是( )
A.①⑤ B.①③⑤ C.②⑤ D.②④⑤
3.下列曲线中,能表示y是x的函数的是( )
A. B.
C. D.
4.已知点在正比例函数的图象上,则的值是( )
A. B. C.6 D.
5.定义:点为平面直角坐标系内的点,若满足,则把点叫做“零点”,例如都是“零点”.当时,直线上有“零点”,则的取值范围是( )
A. B.
C. D.
6.如果两个变量之间关系的图象如图所示,那么随增大而( )
A.增大 B.减小
C.不变 D.有时增大有时减小
7.函数自变量的取值范围是( )
A. B. C. D.
8.若点M(m,n)在一次函数y=﹣5x+b的图象上,且5m+n<3,则b的取值范围为( )
A.b>3 B.b>﹣3 C.b<3 D.b<﹣3
9.如图,用绳子围成周长为的矩形,记矩形的一边长为,它的邻边长为,矩形的面积为.当在一定范围内变化时,和都随的变化而变化,则与,与满足的函数关系分别是( )
A.二次函数关系,一次函数关系
B.一次函数关系,正比例函数关系
C.正比例函数关系,二次函数关系
D.一次函数关系,二次函数关系
10.在平面直角坐标系中,,定义:
(1)A,两点的水平距离
(2)A,两点的垂直距离
(3)A,两点的绝对距离
则下列说法正确的个数是( )
①若,,则,
②若,,,,则或3
③若,,,,均为整数,当代数式取得最大值时,且时,则所有符合条件的点共有26种.
A.0个 B.1个 C.2个 D.3个
二、填空题
11.在函数y=中,自变量x的取值范围是 .
12.直线不经过第一象限,则的取值范围是 .
13.已知一次函数,当自变量时,函数的值可以是 (写出一个合理的值即可).
14.若一次函数的图象过点,则 .
15.点都在直线上,且,则 (填“”或“”)
16.已知王强家、体育场、学校在同一直线上,下面的图像反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中表示时间,表示王强离家的距离.则下列结论正确的是 .(填写所有正确结论的序号)
①体育场离王强家
②王强在体育场锻炼了
③王强吃早餐用了
④王强骑自行车的平均速度是
三、计算题
17.探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:
所挂物体的质量/
弹簧的长度/
(1)当所挂物体的质量为时,弹簧的长度是_______________________;
(2)在弹性限度内如果所挂物体的质量为,弹簧的长度为,根据上表直接写出与的关系式_____________;
(3)当所挂物体的质量为时,请求出弹簧的长度;
(4)如果弹簧的最大长度为,那么该弹簧最多能挂质量为多少的物体?
18.甲、乙两辆摩托车从相距20千米的A、B两地同时出发,相向而行,图中和分别表示甲、乙两辆摩托车离A地的距离s(km)与行驶时间t(h)之间的函数关系.
(1)甲摩托车的速度是______km/h,乙摩托车的速度是______km/h.
(2)何时甲摩托车离B地的距离小于乙摩托车离B地的距离?(写出计算过程)
(3)图中和的交点P表示的含义是什么?写出点P的坐标.
19.【概念感知】
在平面直角坐标系中,如果一个点的纵坐标等于其横坐标的2倍,我们称这个点为“倍值点”.
【概念理解】
(1)求直线上的“倍值点”的坐标;
【概念应用】
(2)如图1,点为抛物线上一点,抛物线上部分的图像记为.将抛物线上部分的图像沿直线翻折得到的图像记为,由图像与组成的图像记为G.
①当时,求图像G上的“倍值点”的坐标;
②当图像G上存在三个“倍值点”,,,且满足,,请直接写出m的值为 .
四、解答题
20.如图,已知反比例函数的图象经过点,过A作轴于点C,经过点C的直线与反比例函数图象交于点B,直线与x轴的负半轴交于点E.
(1)如图1,求m的值.
(2)如图2,若点C是线段的中点,作轴于点D,求的面积.
21.李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图所示.
(1)观察图象,直接写出日销售量的最大值;
(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式.
22.汽车在行驶的过程中,速度往往是变化的.如图表示一辆汽车的速度随时间变化而变化的情况.请根据图象解答下列问题:
(1)在这个变化中,自变量是 ,因变量是 ;
(2)汽车从出发到最后停止共经过了多少时间?
(3)汽车的最高时速是多少?
(4)汽车在哪段时间保持匀速行驶?
23.如图,长方形,以为坐标原点,、分别在轴、轴上,点的坐标为,点的坐标为,点是边上一点,把长方形沿翻折后,点恰好落在轴上点处.
(1)求点E、F的坐标;
(2)求所在直线的函数关系式;
(3)在x轴上求一点P,使成为等腰三角形,请直接写出所有符合条件的点P的坐标.
答案解析部分
1.【答案】D
【知识点】函数自变量的取值范围;用表格表示变量间的关系
2.【答案】A
【知识点】一次函数的概念
3.【答案】A
【知识点】函数的概念;函数的图象
4.【答案】A
【知识点】正比例函数的图象和性质
5.【答案】C
【知识点】一次函数的概念;待定系数法求一次函数解析式
6.【答案】B
【知识点】通过函数图象获取信息
7.【答案】D
【知识点】二次根式有意义的条件;函数自变量的取值范围
8.【答案】C
【知识点】一次函数的性质
9.【答案】D
【知识点】一次函数的概念;二次函数的定义
10.【答案】C
【知识点】点的坐标;坐标与图形性质;待定系数法求一次函数解析式;算术平方根的性质(双重非负性)
11.【答案】
【知识点】分式有无意义的条件;函数自变量的取值范围
12.【答案】
【知识点】一次函数图象、性质与系数的关系
13.【答案】-3(答案不唯一,合理即可)
【知识点】函数值
14.【答案】-2
【知识点】一次函数的图象
15.【答案】
【知识点】一次函数的性质;比较一次函数值的大小
16.【答案】①③④
【知识点】通过函数图象获取信息
17.【答案】(1)
(2)
(3)
(4)
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
18.【答案】(1),
(2)时,甲摩托车离B地的距离小于乙摩托车离B地的距离;
(3)图中和的交点P表示的含义是指两车相遇,点P的坐标为
【知识点】一元一次不等式的应用;一元一次方程的实际应用-行程问题;通过函数图象获取信息
19.【答案】(1)(2)①,,;②或
【知识点】一次函数的概念;坐标与图形变化﹣对称
20.【答案】(1)8
(2)8
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
21.【答案】(1)日销售量的最大值为120千克
(2)李刚家多宝鱼的日销售量y与上市时间x的函数解析式为.
【知识点】待定系数法求一次函数解析式;通过函数图象获取信息;一次函数的其他应用
22.【答案】(1)时间,速度
(2)共经过了分钟
(3)最高时速是
(4)在至分钟保持匀速行驶
【知识点】函数的概念;通过函数图象获取信息
23.【答案】(1),
(2)
(3)P的坐标为或或或
【知识点】坐标与图形性质;待定系数法求一次函数解析式;等腰三角形的判定与性质;矩形的性质
21世纪教育网(www.21cnjy.com)
1 / 9
第四章 一次函数【培优】
一、单选题
1.弹簧挂上物体后会伸长,测得弹簧的长度()与所挂的物体的质量()之间有下面的关系:
下列说法不正确的是( ).
A.与都是变量,且是自变量,是因变量
B.所挂物体质量为时,弹簧长度为
C.物体质量每增加,弹簧长度增加
D.弹簧不挂重物时的长度为
2.下列函数关系式:①,②,③,④,⑤,其中是一次函数的是( )
A.①⑤ B.①③⑤ C.②⑤ D.②④⑤
3.下列曲线中,能表示y是x的函数的是( )
A. B.
C. D.
4.已知点在正比例函数的图象上,则的值是( )
A. B. C.6 D.
5.定义:点为平面直角坐标系内的点,若满足,则把点叫做“零点”,例如都是“零点”.当时,直线上有“零点”,则的取值范围是( )
A. B.
C. D.
6.如果两个变量之间关系的图象如图所示,那么随增大而( )
A.增大 B.减小
C.不变 D.有时增大有时减小
7.函数自变量的取值范围是( )
A. B. C. D.
8.若点M(m,n)在一次函数y=﹣5x+b的图象上,且5m+n<3,则b的取值范围为( )
A.b>3 B.b>﹣3 C.b<3 D.b<﹣3
9.如图,用绳子围成周长为的矩形,记矩形的一边长为,它的邻边长为,矩形的面积为.当在一定范围内变化时,和都随的变化而变化,则与,与满足的函数关系分别是( )
A.二次函数关系,一次函数关系
B.一次函数关系,正比例函数关系
C.正比例函数关系,二次函数关系
D.一次函数关系,二次函数关系
10.在平面直角坐标系中,,定义:
(1)A,两点的水平距离
(2)A,两点的垂直距离
(3)A,两点的绝对距离
则下列说法正确的个数是( )
①若,,则,
②若,,,,则或3
③若,,,,均为整数,当代数式取得最大值时,且时,则所有符合条件的点共有26种.
A.0个 B.1个 C.2个 D.3个
二、填空题
11.在函数y=中,自变量x的取值范围是 .
12.直线不经过第一象限,则的取值范围是 .
13.已知一次函数,当自变量时,函数的值可以是 (写出一个合理的值即可).
14.若一次函数的图象过点,则 .
15.点都在直线上,且,则 (填“”或“”)
16.已知王强家、体育场、学校在同一直线上,下面的图像反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中表示时间,表示王强离家的距离.则下列结论正确的是 .(填写所有正确结论的序号)
①体育场离王强家
②王强在体育场锻炼了
③王强吃早餐用了
④王强骑自行车的平均速度是
三、计算题
17.探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:
所挂物体的质量/
弹簧的长度/
(1)当所挂物体的质量为时,弹簧的长度是_______________________;
(2)在弹性限度内如果所挂物体的质量为,弹簧的长度为,根据上表直接写出与的关系式_____________;
(3)当所挂物体的质量为时,请求出弹簧的长度;
(4)如果弹簧的最大长度为,那么该弹簧最多能挂质量为多少的物体?
18.甲、乙两辆摩托车从相距20千米的A、B两地同时出发,相向而行,图中和分别表示甲、乙两辆摩托车离A地的距离s(km)与行驶时间t(h)之间的函数关系.
(1)甲摩托车的速度是______km/h,乙摩托车的速度是______km/h.
(2)何时甲摩托车离B地的距离小于乙摩托车离B地的距离?(写出计算过程)
(3)图中和的交点P表示的含义是什么?写出点P的坐标.
19.【概念感知】
在平面直角坐标系中,如果一个点的纵坐标等于其横坐标的2倍,我们称这个点为“倍值点”.
【概念理解】
(1)求直线上的“倍值点”的坐标;
【概念应用】
(2)如图1,点为抛物线上一点,抛物线上部分的图像记为.将抛物线上部分的图像沿直线翻折得到的图像记为,由图像与组成的图像记为G.
①当时,求图像G上的“倍值点”的坐标;
②当图像G上存在三个“倍值点”,,,且满足,,请直接写出m的值为 .
四、解答题
20.如图,已知反比例函数的图象经过点,过A作轴于点C,经过点C的直线与反比例函数图象交于点B,直线与x轴的负半轴交于点E.
(1)如图1,求m的值.
(2)如图2,若点C是线段的中点,作轴于点D,求的面积.
21.李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图所示.
(1)观察图象,直接写出日销售量的最大值;
(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式.
22.汽车在行驶的过程中,速度往往是变化的.如图表示一辆汽车的速度随时间变化而变化的情况.请根据图象解答下列问题:
(1)在这个变化中,自变量是 ,因变量是 ;
(2)汽车从出发到最后停止共经过了多少时间?
(3)汽车的最高时速是多少?
(4)汽车在哪段时间保持匀速行驶?
23.如图,长方形,以为坐标原点,、分别在轴、轴上,点的坐标为,点的坐标为,点是边上一点,把长方形沿翻折后,点恰好落在轴上点处.
(1)求点E、F的坐标;
(2)求所在直线的函数关系式;
(3)在x轴上求一点P,使成为等腰三角形,请直接写出所有符合条件的点P的坐标.
答案解析部分
1.【答案】D
【知识点】函数自变量的取值范围;用表格表示变量间的关系
2.【答案】A
【知识点】一次函数的概念
3.【答案】A
【知识点】函数的概念;函数的图象
4.【答案】A
【知识点】正比例函数的图象和性质
5.【答案】C
【知识点】一次函数的概念;待定系数法求一次函数解析式
6.【答案】B
【知识点】通过函数图象获取信息
7.【答案】D
【知识点】二次根式有意义的条件;函数自变量的取值范围
8.【答案】C
【知识点】一次函数的性质
9.【答案】D
【知识点】一次函数的概念;二次函数的定义
10.【答案】C
【知识点】点的坐标;坐标与图形性质;待定系数法求一次函数解析式;算术平方根的性质(双重非负性)
11.【答案】
【知识点】分式有无意义的条件;函数自变量的取值范围
12.【答案】
【知识点】一次函数图象、性质与系数的关系
13.【答案】-3(答案不唯一,合理即可)
【知识点】函数值
14.【答案】-2
【知识点】一次函数的图象
15.【答案】
【知识点】一次函数的性质;比较一次函数值的大小
16.【答案】①③④
【知识点】通过函数图象获取信息
17.【答案】(1)
(2)
(3)
(4)
【知识点】用表格表示变量间的关系;用关系式表示变量间的关系
18.【答案】(1),
(2)时,甲摩托车离B地的距离小于乙摩托车离B地的距离;
(3)图中和的交点P表示的含义是指两车相遇,点P的坐标为
【知识点】一元一次不等式的应用;一元一次方程的实际应用-行程问题;通过函数图象获取信息
19.【答案】(1)(2)①,,;②或
【知识点】一次函数的概念;坐标与图形变化﹣对称
20.【答案】(1)8
(2)8
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
21.【答案】(1)日销售量的最大值为120千克
(2)李刚家多宝鱼的日销售量y与上市时间x的函数解析式为.
【知识点】待定系数法求一次函数解析式;通过函数图象获取信息;一次函数的其他应用
22.【答案】(1)时间,速度
(2)共经过了分钟
(3)最高时速是
(4)在至分钟保持匀速行驶
【知识点】函数的概念;通过函数图象获取信息
23.【答案】(1),
(2)
(3)P的坐标为或或或
【知识点】坐标与图形性质;待定系数法求一次函数解析式;等腰三角形的判定与性质;矩形的性质
21世纪教育网(www.21cnjy.com)
1 / 9
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
