人教版五年级下册数学质数和合数(课件)(共43张PPT)
文档属性
| 名称 | 人教版五年级下册数学质数和合数(课件)(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 21:26:32 | ||
图片预览









文档简介
(共43张PPT)
人教版数学五年级下册
质数和合数
输入标题
学习目标
经历探究100以内质数的学习过程,培养学生观察比较和有序思考的探究能力。
理解质数与合数的意义,并能正确辨析。知道100以内的质数,熟悉20以内的质数。
准备好了吗?一起去探索吧!
在学习活动中体验数学知识之间的内在联系,感受学习数学的乐趣。
奇数 1 3 5 7 9 11 13 15 17 19
偶数 2 4 6 8 10 12 14 16 18 20
输入标题
关于因数和倍数还有什么要注意吗?
12是2和6的倍数,2和6是12的因数。
因数和倍数是相互依存的。
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数。
研究因数和倍数的时候,我们所说的数指的是非0自然数。
回顾一下,什么是因数和倍数?
12÷2=6
一、复习旧知,导入新课。
抢答:请同学们以最快的速度说出下面的数有几个因数。
找因数
2
2
5
2
1
1
9
3
11
2
数
因数的个数
找因数
1.一个数的最小因数是几?最大因数是几?
一个数因数的个数是有限的。
一个数是最小因数是1,最大因数是它本身。
2.一个数的因数是有限的还是无限的?
3.怎样找一个数的因数?
找一个数的因数,用这个数依次除以1,2,3,4……商如果是整数,除数和商都是这个数的因数。
试一试:找出 1~20各数的因数。
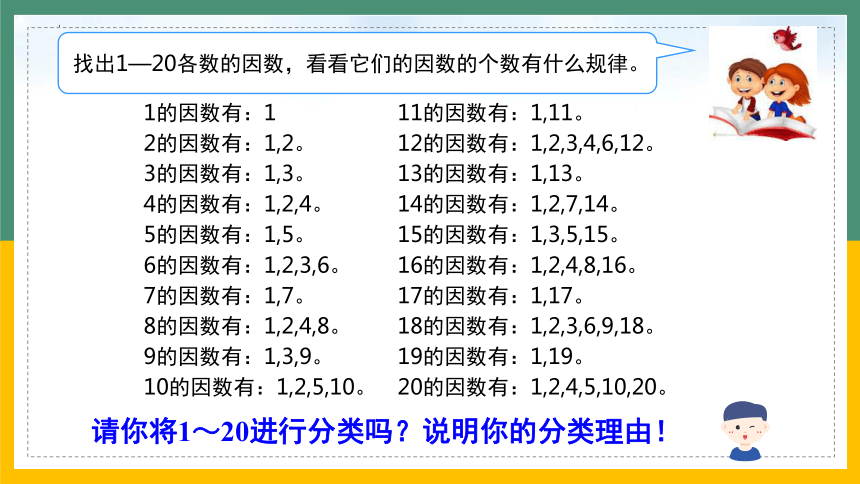
找出1—20各数的因数,看看它们的因数的个数有什么规律。
1的因数有:1
2的因数有:1,2。
3的因数有:1,3。
4的因数有:1,2,4。
5的因数有:1,5。
6的因数有:1,2,3,6。
7的因数有:1,7。
8的因数有:1,2,4,8。
9的因数有:1,3,9。
10的因数有:1,2,5,10。
11的因数有:1,11。
12的因数有:1,2,3,4,6,12。
13的因数有:1,13。
14的因数有:1,2,7,14。
18的因数有:1,2,3,6,9,18。
15的因数有:1,3,5,15。
16的因数有:1,2,4,8,16。
17的因数有:1,17。
19的因数有:1,19。
20的因数有:1,2,4,5,10,20。
请你将1~20进行分类吗?说明你的分类理由!
找出1~20各数的因数。根据因数的个数进行分类,并填写下表。
只有一个因数的数 只有1和它本身两个因数的数 有两个以上因数的数
学法指导:独立完成,小组讨论,个人展示。
质数和合数
小组活动(3分钟)
观察它们因数的个数,你发现了什么?
小组讨论:根据因数的个数,你觉得可以怎样分类?
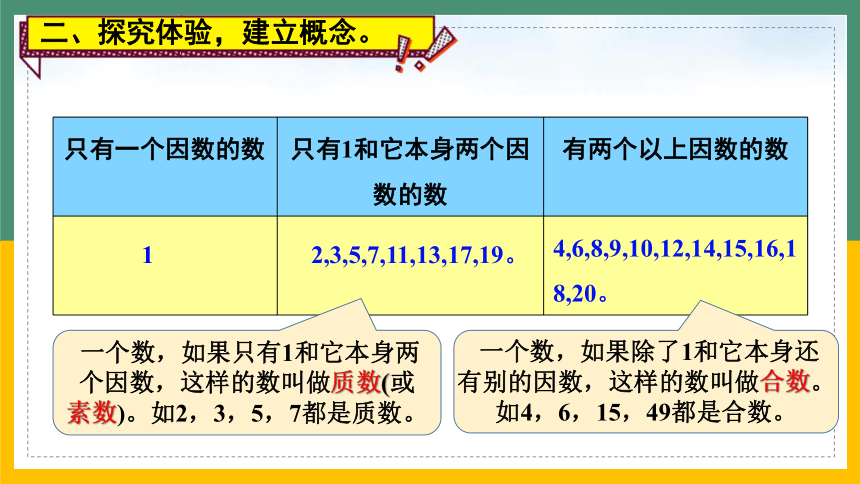
只有一个因数的数 只有1和它本身两个因数的数 有两个以上因数的数
1
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。如2,3,5,7都是质数。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。如4,6,15,49都是合数。
2,3,5,7,11,13,17,19。
4,6,8,9,10,12,14,15,16,18,20。
二、探究体验,建立概念。
10,
14,
15,
8,
9,
12,
16,
把1~20各数可以怎样分类?
奇数:1,3,5,7,9,11,13,15,17,19。
偶数:2,4,6,8,10,12,14,16,18,20。
质数:
3,5,7,11,13,17,19。
2,
合数:
4,
6,
18,
20。
1既不是质数,也不是合数。
最小
2是最小的质数。
2是偶数里面唯一的质数。
4是最小的合数。
熟记 20 以内的质数:
2,3,5,7,11,13,17,19
自然数
质数
合数
1
只有1和本身两个因数
至少有3个因数
既不是质数也不是合数
三、拓展深化,100内质数表。
找出100以内的质数,做一个质数表。
01
02
阐述你的制作方法
小组合作
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
可以逐一验证每个数,看哪些是质数。
先把2的倍数划去,2除外,划掉的这些数都不是质数。再把3的倍数划去。
想一想:划到几的倍数就可以了?
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
找出100以内的质数,做一个质数表。
先把2的倍数画去,但2除外,画掉的这些数都不是质数。
再把3的倍数画去,但3除外,画掉的这些数都不是质数。
又把5的倍数画去,但5除外,画掉的这些数都不是质数。
最后把7的倍数画去,但7除外,画掉的这些数都不是质数。
画到几的倍数就可以了?
做质数表
探索新知
2 3 5 7 11
13 17 19 23 29
31 37 41 43 47
53 59 61 67 71
73 79 83 89 97
100以内质数表
合数
1
2
奇数 偶数
合数
质数
自 然 数
输入标题
自主探究
自然数
(按因数的个数分类)
质数
合数
1
自然数
(按是否是2的倍数分类)
奇数
偶数
思考:自然数可以怎样分类。
探索新知
知识点
两数之和的奇偶性
奇数与偶数的和是奇数还是偶数?奇数与奇数的和是奇数还是偶数?偶数与偶数的和呢?
想一想,应该怎么做呢?
阅读与理解
从题目中你知道了什么?
题目让我们对奇数、偶数的和做一些探索。
奇数+偶数=
奇数
偶数?
奇数+奇数=
奇数?
偶数?
偶数+偶数=
奇数?
偶数?
我把问题表示成这样……。
分析与解答
我随便找几个奇数、偶数,加起来看一看。
奇数:5, 7, 9, 11,…。
偶数:8,12,20,24,…。
分析与解答
5+8=13,7+8=15,9+8=17。
……
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
5+7=12,7+9=16,9+11=20。
……
8+12=20,12+20=32,20+24=44。
……
探索新知
奇数除以2余1,偶数除以2没有余数。
奇数:
……
偶数:
……
奇数加偶数的和除以2还余1,所以,奇数+偶数=奇数。
奇数加奇数的和除以2没有余数,所以,奇数+奇数=偶数。
偶数加偶数的和除以2没有余数,所以,偶数+偶数=偶数。
回顾与反思
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
这个结论正确吗?
534+319=853
所以,奇数+偶数=奇数。
我可以再找一些大数试一试。
将下面的各数分别填入指定的圈内。
牛刀小试。
37
11
61
73
83
2
27
58
95
27
37
11
61
73
2 27 37 11 58 61 73 83 95
质数
合数
奇数
偶数
83
95
2
58
看看除了1和本身外,是否有第三个因数,有就是合数,没有就是质数。
怎样判断又准确又快?
牛刀小试。
两个质数,和是10,积是21,这两个质数是多少?
两个质数,和是7,积是10,这两个质数是多少?
21=3×7,3和7都是质数,而且3+7=10,所以这两个质数就是3和7。
10=2×5,2和5都是质数,而且2+5=7,所以这两个质数就是2和5。
归纳总结
判断一个数是不是质数的基本步骤:
第一步:看是不是2、3、5的倍数,除了2、3、5本身以外,是2、3、5的倍数的数就不是质数;
第二步:由小到大分别用其它质数(如7、11、13……)去除这个数,看商是否是整数,如果商是整数,这个数就不是质数;
第三步:找到两个相同数,它俩积略大于或等于这个数,直到试除的质数是小于这两个相同数的最大质数为止。
四、实践应用,反馈评价。
一. 将下面各数分别填入指定的圈里。
37
41
61
73
83
11
47
27
58
95
14
33
57
62
87
99
27
37
41
61
73
83
95
11
47
57
87
99
58
14
62
33
27 37 41 58 61 73 83 95
11 14 33 47 57 62 87 99
质数
合数
偶数
奇数
二、辨一辨。(对的画“√”, 错的画“×”)
1.一个数可以既是合数又是质数。 ( )
2.自然数中,是2的倍数的数叫作合数。 ( )
3.一个合数至少有三个因数,它的最大因数与最小倍数相等。 ( )
4.自然数可分为奇数和偶数,也可以分为质数和合数。( )
5.2是偶数,也是合数。 ( )
×
×
√
×
×
三、巧虎在侦破一个案件时发现了一个保险箱,保险箱设有六位数的密码:
已知:A是5最大的因数;B的所有因数是1、2、4、8;C是最小的自然数;D只有一个因数;E既是质数,又是偶数;F既是9的因数,又是9的倍数,这个保险箱的密码是( ).
A
B
C
D
E
F
580129
猜猜我是谁。
我们两个的和是8。
我们两个的积是15。
将15写成两个质数相乘的形式,然后把两个质数相加,使结果等于8。
这两个质数分别是3和5。
15=3×5
3+5=8
算一算。
3个不同质数的和是最小合数的平方,这3个质数的积是多少?
2+3+11=16
最小的合数是4,4 =16。
哪3个质数的和是16呢?
2×3×11=66
答:这3个质数的积是66。
1.填空。
(1)最小的自然数是( ),最小的奇数是( )。
最小的质数是( ),最小的偶数是( )。
最小的合数是( )。
(2)既是奇数又是质数的最小自然数是( )。
既是偶数又是合数的最小自然数是( )。
既是奇数又是合数的最小自然数是( )。
0
1
2
0
4
4
3
9
2.从0,2,3,5,7中任选两个数组成一个两位数,按要求填在括号里。
质数( )
合数( )
23,37,53,73。
20,25,27,30,32,35,50,52,57,70,72,75。
一个质数是两位数,个位和十位上的数字都是质数,个位和十位上的数字交换后,还是质数。这个两位数是多少?
37
73
1~10十个数字中质数有2、3、5、7。
答:这个两位数是37或73。
我国的数学家陈景润已经证明了任何一个充分大的偶数都可以表示为一个质数加上两个质数的积。例如:8=2+2×3,20=5+3×5......这称为陈氏定理,在国际数学界引起了强烈的反响。但彻底证明哥德巴赫猜想还差最后一步,这最后一步称为数学皇冠上的明珠。
二百多年前,德国有一位名叫哥德巴赫的数学家。他发现任何一个大于4的偶数,都可以写成两个质数的和。例如:6=3+3,10 =3+7,12=5+7......因为这个问题他还没有证明出来,人们把它称为哥德巴赫猜想。
课堂总结
通过这节课的学习,你有什么收获?
同学们,这节课你有哪些收获?
质数和合数
1. 一个数,如果只有1和它本身两个因数的数,那么这样的数叫做质数(或素数)。
2.一个数,如果除了1和本身还有别的因数,那么这样的数叫做合数。
3.1既不是质数,也不是合数。2是最小的质数,4是最小的合数。
同学们,今天的数学课你们有哪些收获呢?
五、实践应用,反馈评价
人教版数学五年级下册
谢谢聆听
同学们再见
人教版数学五年级下册
质数和合数
输入标题
学习目标
经历探究100以内质数的学习过程,培养学生观察比较和有序思考的探究能力。
理解质数与合数的意义,并能正确辨析。知道100以内的质数,熟悉20以内的质数。
准备好了吗?一起去探索吧!
在学习活动中体验数学知识之间的内在联系,感受学习数学的乐趣。
奇数 1 3 5 7 9 11 13 15 17 19
偶数 2 4 6 8 10 12 14 16 18 20
输入标题
关于因数和倍数还有什么要注意吗?
12是2和6的倍数,2和6是12的因数。
因数和倍数是相互依存的。
在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数。
研究因数和倍数的时候,我们所说的数指的是非0自然数。
回顾一下,什么是因数和倍数?
12÷2=6
一、复习旧知,导入新课。
抢答:请同学们以最快的速度说出下面的数有几个因数。
找因数
2
2
5
2
1
1
9
3
11
2
数
因数的个数
找因数
1.一个数的最小因数是几?最大因数是几?
一个数因数的个数是有限的。
一个数是最小因数是1,最大因数是它本身。
2.一个数的因数是有限的还是无限的?
3.怎样找一个数的因数?
找一个数的因数,用这个数依次除以1,2,3,4……商如果是整数,除数和商都是这个数的因数。
试一试:找出 1~20各数的因数。
找出1—20各数的因数,看看它们的因数的个数有什么规律。
1的因数有:1
2的因数有:1,2。
3的因数有:1,3。
4的因数有:1,2,4。
5的因数有:1,5。
6的因数有:1,2,3,6。
7的因数有:1,7。
8的因数有:1,2,4,8。
9的因数有:1,3,9。
10的因数有:1,2,5,10。
11的因数有:1,11。
12的因数有:1,2,3,4,6,12。
13的因数有:1,13。
14的因数有:1,2,7,14。
18的因数有:1,2,3,6,9,18。
15的因数有:1,3,5,15。
16的因数有:1,2,4,8,16。
17的因数有:1,17。
19的因数有:1,19。
20的因数有:1,2,4,5,10,20。
请你将1~20进行分类吗?说明你的分类理由!
找出1~20各数的因数。根据因数的个数进行分类,并填写下表。
只有一个因数的数 只有1和它本身两个因数的数 有两个以上因数的数
学法指导:独立完成,小组讨论,个人展示。
质数和合数
小组活动(3分钟)
观察它们因数的个数,你发现了什么?
小组讨论:根据因数的个数,你觉得可以怎样分类?
只有一个因数的数 只有1和它本身两个因数的数 有两个以上因数的数
1
一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。如2,3,5,7都是质数。
一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。如4,6,15,49都是合数。
2,3,5,7,11,13,17,19。
4,6,8,9,10,12,14,15,16,18,20。
二、探究体验,建立概念。
10,
14,
15,
8,
9,
12,
16,
把1~20各数可以怎样分类?
奇数:1,3,5,7,9,11,13,15,17,19。
偶数:2,4,6,8,10,12,14,16,18,20。
质数:
3,5,7,11,13,17,19。
2,
合数:
4,
6,
18,
20。
1既不是质数,也不是合数。
最小
2是最小的质数。
2是偶数里面唯一的质数。
4是最小的合数。
熟记 20 以内的质数:
2,3,5,7,11,13,17,19
自然数
质数
合数
1
只有1和本身两个因数
至少有3个因数
既不是质数也不是合数
三、拓展深化,100内质数表。
找出100以内的质数,做一个质数表。
01
02
阐述你的制作方法
小组合作
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
可以逐一验证每个数,看哪些是质数。
先把2的倍数划去,2除外,划掉的这些数都不是质数。再把3的倍数划去。
想一想:划到几的倍数就可以了?
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
找出100以内的质数,做一个质数表。
先把2的倍数画去,但2除外,画掉的这些数都不是质数。
再把3的倍数画去,但3除外,画掉的这些数都不是质数。
又把5的倍数画去,但5除外,画掉的这些数都不是质数。
最后把7的倍数画去,但7除外,画掉的这些数都不是质数。
画到几的倍数就可以了?
做质数表
探索新知
2 3 5 7 11
13 17 19 23 29
31 37 41 43 47
53 59 61 67 71
73 79 83 89 97
100以内质数表
合数
1
2
奇数 偶数
合数
质数
自 然 数
输入标题
自主探究
自然数
(按因数的个数分类)
质数
合数
1
自然数
(按是否是2的倍数分类)
奇数
偶数
思考:自然数可以怎样分类。
探索新知
知识点
两数之和的奇偶性
奇数与偶数的和是奇数还是偶数?奇数与奇数的和是奇数还是偶数?偶数与偶数的和呢?
想一想,应该怎么做呢?
阅读与理解
从题目中你知道了什么?
题目让我们对奇数、偶数的和做一些探索。
奇数+偶数=
奇数
偶数?
奇数+奇数=
奇数?
偶数?
偶数+偶数=
奇数?
偶数?
我把问题表示成这样……。
分析与解答
我随便找几个奇数、偶数,加起来看一看。
奇数:5, 7, 9, 11,…。
偶数:8,12,20,24,…。
分析与解答
5+8=13,7+8=15,9+8=17。
……
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
5+7=12,7+9=16,9+11=20。
……
8+12=20,12+20=32,20+24=44。
……
探索新知
奇数除以2余1,偶数除以2没有余数。
奇数:
……
偶数:
……
奇数加偶数的和除以2还余1,所以,奇数+偶数=奇数。
奇数加奇数的和除以2没有余数,所以,奇数+奇数=偶数。
偶数加偶数的和除以2没有余数,所以,偶数+偶数=偶数。
回顾与反思
奇数+奇数=偶数
奇数+偶数=奇数
偶数+偶数=偶数
这个结论正确吗?
534+319=853
所以,奇数+偶数=奇数。
我可以再找一些大数试一试。
将下面的各数分别填入指定的圈内。
牛刀小试。
37
11
61
73
83
2
27
58
95
27
37
11
61
73
2 27 37 11 58 61 73 83 95
质数
合数
奇数
偶数
83
95
2
58
看看除了1和本身外,是否有第三个因数,有就是合数,没有就是质数。
怎样判断又准确又快?
牛刀小试。
两个质数,和是10,积是21,这两个质数是多少?
两个质数,和是7,积是10,这两个质数是多少?
21=3×7,3和7都是质数,而且3+7=10,所以这两个质数就是3和7。
10=2×5,2和5都是质数,而且2+5=7,所以这两个质数就是2和5。
归纳总结
判断一个数是不是质数的基本步骤:
第一步:看是不是2、3、5的倍数,除了2、3、5本身以外,是2、3、5的倍数的数就不是质数;
第二步:由小到大分别用其它质数(如7、11、13……)去除这个数,看商是否是整数,如果商是整数,这个数就不是质数;
第三步:找到两个相同数,它俩积略大于或等于这个数,直到试除的质数是小于这两个相同数的最大质数为止。
四、实践应用,反馈评价。
一. 将下面各数分别填入指定的圈里。
37
41
61
73
83
11
47
27
58
95
14
33
57
62
87
99
27
37
41
61
73
83
95
11
47
57
87
99
58
14
62
33
27 37 41 58 61 73 83 95
11 14 33 47 57 62 87 99
质数
合数
偶数
奇数
二、辨一辨。(对的画“√”, 错的画“×”)
1.一个数可以既是合数又是质数。 ( )
2.自然数中,是2的倍数的数叫作合数。 ( )
3.一个合数至少有三个因数,它的最大因数与最小倍数相等。 ( )
4.自然数可分为奇数和偶数,也可以分为质数和合数。( )
5.2是偶数,也是合数。 ( )
×
×
√
×
×
三、巧虎在侦破一个案件时发现了一个保险箱,保险箱设有六位数的密码:
已知:A是5最大的因数;B的所有因数是1、2、4、8;C是最小的自然数;D只有一个因数;E既是质数,又是偶数;F既是9的因数,又是9的倍数,这个保险箱的密码是( ).
A
B
C
D
E
F
580129
猜猜我是谁。
我们两个的和是8。
我们两个的积是15。
将15写成两个质数相乘的形式,然后把两个质数相加,使结果等于8。
这两个质数分别是3和5。
15=3×5
3+5=8
算一算。
3个不同质数的和是最小合数的平方,这3个质数的积是多少?
2+3+11=16
最小的合数是4,4 =16。
哪3个质数的和是16呢?
2×3×11=66
答:这3个质数的积是66。
1.填空。
(1)最小的自然数是( ),最小的奇数是( )。
最小的质数是( ),最小的偶数是( )。
最小的合数是( )。
(2)既是奇数又是质数的最小自然数是( )。
既是偶数又是合数的最小自然数是( )。
既是奇数又是合数的最小自然数是( )。
0
1
2
0
4
4
3
9
2.从0,2,3,5,7中任选两个数组成一个两位数,按要求填在括号里。
质数( )
合数( )
23,37,53,73。
20,25,27,30,32,35,50,52,57,70,72,75。
一个质数是两位数,个位和十位上的数字都是质数,个位和十位上的数字交换后,还是质数。这个两位数是多少?
37
73
1~10十个数字中质数有2、3、5、7。
答:这个两位数是37或73。
我国的数学家陈景润已经证明了任何一个充分大的偶数都可以表示为一个质数加上两个质数的积。例如:8=2+2×3,20=5+3×5......这称为陈氏定理,在国际数学界引起了强烈的反响。但彻底证明哥德巴赫猜想还差最后一步,这最后一步称为数学皇冠上的明珠。
二百多年前,德国有一位名叫哥德巴赫的数学家。他发现任何一个大于4的偶数,都可以写成两个质数的和。例如:6=3+3,10 =3+7,12=5+7......因为这个问题他还没有证明出来,人们把它称为哥德巴赫猜想。
课堂总结
通过这节课的学习,你有什么收获?
同学们,这节课你有哪些收获?
质数和合数
1. 一个数,如果只有1和它本身两个因数的数,那么这样的数叫做质数(或素数)。
2.一个数,如果除了1和本身还有别的因数,那么这样的数叫做合数。
3.1既不是质数,也不是合数。2是最小的质数,4是最小的合数。
同学们,今天的数学课你们有哪些收获呢?
五、实践应用,反馈评价
人教版数学五年级下册
谢谢聆听
同学们再见
