3.6三角形中位线

课件19张PPT。三角形、梯形中位线（1） 主讲教师：陈言富
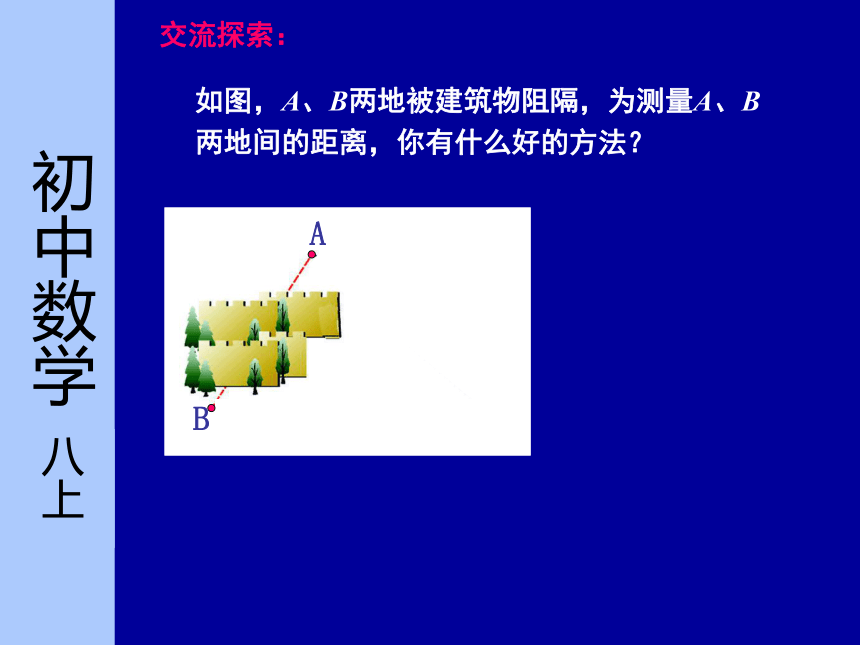
宝应县射阳湖镇中心初级中学初中数学八年级 上册 (苏科版)第三章 第六节如图，A、B两地被建筑物阻隔，为测量A、B两地间的距离，你有什么好的方法？AB交流探索：　　怎样将一张三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形?FADCBE四边形BCFD是平行四边形吗?为什么?动手做一做四边形BCFD是平行四边形.
由中心对称得：FC = AD，∠CFE=∠ADE.
所以 AB∥FC．
由 DB=AD，FC=AD，得 DB=FC.
所以四边形BCFD是平行四边形.FADCBE四边形BCFD是平行四边形吗?为什么?　　连接三角形两边中点的线段，叫做三角形的中位线．（2）如果DE为△ABC的中位线，那么D、E分别为AB、AC 的　　　　． （1）如果D、E分别为AB、AC的中点，那么DE为△ABC的 　　 ；中位线中点　三角形的中位线的定义：　　三角形的中位线是连接三角形两边中点的线段．三角形的中线是连接一个顶点和它的对边中点的线段．　　1.画出△ABC，作出它的所有中位线，并指出一个三角形有几条中位线.　　2.在上题的图中作出三角形的所有中线，并说明中线和中位线有何不同．ABCDEF动手画一画线段1个三角形共有3条中位线．　　DE是△ABC的中位线，猜想DE与BC有怎样的位置关系和数量关系? 为什么?FADCBE量一量、想一想又由四边形BCFD是平行四边形，得DE∥BC，DE=BC由△ADE≌△CFE，得EF=DE= DF.DE= DF= BC.DE∥BC，DE＝　BC．三角形的中位线平行于第三边，并且等于它的一半．三角形的中位线性质：　　因为 D、E分别是AB、AC的中点所以 DE∥BC， DE =　　BC．所以 DE是△ABC的中位线　　例1.在△ABC中，AB=10 cm, AC=8 cm, BC=9 cm．44.55答案：13.5 cm细心练一练DEF（1）求连接各边中点所成三角形的周长.解：　　∵ D、E分别是AB、AC的中点∴ DE是△ABC的中位线∴ DE= BC．　　∵ BC = 9 cm　　∴ DE = 4.5 cm（2）在上小题的基础你还能得到那些结论? 四边形ADFE、四边形DCFE和四边形DFBE都是平行四边形；四个小三角形两两全等，每个小三角形的周长是原三角形的一半，面积是原三角形的 等． 细心练一练DEF例2.如图，A、B两地被建筑物阻隔，为测量A、B两地间的距离，你有什么好的方法？C（1）若DE的长为36 m，求A、B两地间的距离；在地面上选一点C，ABDE分别取CA、CB的中点D、E，连接CA、CB，方法：连接DE.利用△ABC的中位线定理得：AB=2DE=72 m（2）如果D、E两点间还有阻隔，你有解决问题的办法吗?　　请大家课后想一想，你还能想出其它测量AB的方法吗?例2 如图，A、B两地被建筑物阻隔，为测量A、B两地间的距离，在地面上选一点C，连接CA、CB，分别取CA、CB的中点D、E.　　例3 如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点．四边形EFGH是平行四边形吗?为什么?解：∵ E、F分别是AB、BC的中点连接AC．∴ 四边形EFGH是平行四边形．∴ EF∥AC，EF = 　AC．　同理可以得到：　∴ EF∥HG，EF=HG．　四边形EFGH是平行四边形．∴ EF是△ABC的中位线
HG∥AC，HG =　 AC．　　　1.顺次连结矩形四边中点所得的四边是　　　　　；　　2.顺次连结菱形四边中点所得的四边形是　　　　.菱形矩形画一画、想一想　　例4 如图，在平行四边形ABCD中，E、F分别是AB、CD上的点，且AE＝DF．
试说明： GH∥AB，GH = 　AB．　 顺次连接任意四边形各边中点，所得的四边形是平行四边形．　　顺次连接四边形各边中点，那么所得新四边形的形状与原四边形的对角线有什么关系? 思考题　　1.通过本节课的学习，知道了连接三角形两边的中点的线段叫做三角形的中位线．
　　2.三角形中位线的性质：三角形的中位线平行于第三边(位置关系)，并且等于它的一半(数量关系)．
　　　　课堂小结1.理解并背诵三角形的中位线定义和性质；
　　　　布置作业2.完成课堂检测试卷 ，第1～7题 ，第8、9题
课后完成。
　　　　老师、同学们：
再见！