湖南省长沙市麓山国际实验学校2016届九年级第六次限时训练数学试题
文档属性
| 名称 | 湖南省长沙市麓山国际实验学校2016届九年级第六次限时训练数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 151.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-25 00:00:00 | ||
图片预览



文档简介
麓山国际实验学校2015—2016—2初三第六次限时训练
数 学 试 卷
总 分:120分 时 量 :120分钟
一.选择题(3×12分=36分)
1、下列四个实数中是无理数的是( )
A.π B. C. D.0
2、下列图形中,是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3、已知空气的单位体积质量为克/厘米3,用小数表示为( )
A.0.00129 B.0.0129 C.-0.00129 D.0.000129
4、下列计算正确的是( )
A. B. C. D.
5、点P(4,﹣3)到轴的距离是( )
A.4 B.3 C.﹣3 D.5
6、我区某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )
班级 1班 2班 3班 4班 5班 6班
人数 52 60 62 54 58 62
A. 平均数是60 B. 中位数是59 C. 极差是40 D. 众数是58
7、抛物线的顶点坐标为( )
A.(1,-3) B.(-1,3) C.(-1,-3) D. (1,3)
8、若关于的一元二次方程有两个实数根,则的取值范围是( )
A. B. C. D. 且
9、为了控制房价,最近很多城市出台了房产购买限制措施,假设某人购买某处房子原来需支付首付款30%,即27万元,现在按照新规定首付款必须不低于50%,则这个人按照新规定至少支付首付款( )
A.13.5万元 B.45万元 C.54万元 D.100万元
10、一副三角板有两个直角三角形,如图叠放在一起,则∠的度数是( )
A.165° B.120° C.150° D.135°
11、如图,在平面直角坐标系中,点A在第一象限,⊙A与轴相切于B,与轴交于C(0,1)、D(0,4)两点,则点A的坐标是 ( )
A. B. C. D.
12、如图,将矩形ABCD沿对角线折叠,使落在处,交于,则下列结论不一定成立的是( )
A. B. C. D.
第10题图
二 、填空题(3分×6=18分)
13、分解因式:= .
14、若是方程的解,则的值为
15、已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为,则a等于
16、如图,△ABC中,DE∥BC,AE:EB=2:3,则DE:BC= .
17、某水库堤坝的横断面如图,迎水坡AB的坡度是1:,堤坝高BC=50m,则AB= m.
18、如图,在Rt△ABC中,,AB=AC=,点E为AC的中点,点F在底边BC上,且,则△的面积为
16题 17题
三、解答题(6小题,共46分)
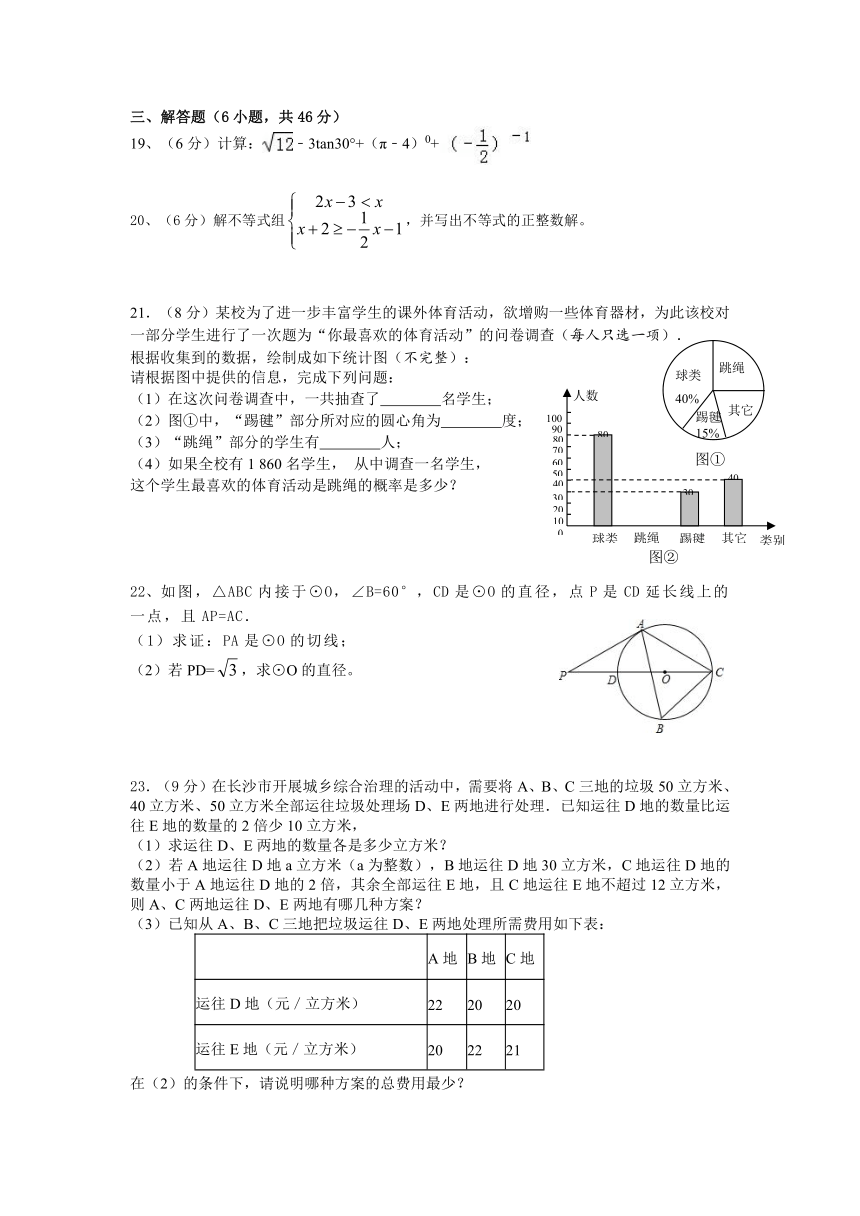
19、(6分)计算:﹣3tan30°+(π﹣4)0+
20、(6分)解不等式组,并写出不等式的正整数解。
21.(8分)某校为了进一步丰富学生的课外体育活动,欲增购一些体育器材,为此该校对一部分学生进行了一次题为“你最喜欢的体育活动”的问卷调查(每人只选一项).
根据收集到的数据,绘制成如下统计图(不完整):
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,一共抽查了 名学生;
(2)图①中,“踢毽”部分所对应的圆心角为 度;
(3)“跳绳”部分的学生有 人;
(4)如果全校有1 860名学生, 从中调查一名学生,
这个学生最喜欢的体育活动是跳绳的概率是多少?
22、如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=,求⊙O的直径。
23.(9分)在长沙市开展城乡综合治理的活动中,需要将A、B、C三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场D、E两地进行处理.已知运往D地的数量比运往E地的数量的2倍少10立方米,
(1)求运往D、E两地的数量各是多少立方米?
(2)若A地运往D地a立方米(a为整数),B地运往D地30立方米,C地运往D地的数量小于A地运往D地的2倍,其余全部运往E地,且C地运往E地不超过12立方米,则A、C两地运往D、E两地有哪几种方案?
(3)已知从A、B、C三地把垃圾运往D、E两地处理所需费用如下表:
A地 B地 C地
运往D地(元/立方米) 22 20 20
运往E地(元/立方米) 20 22 21
在(2)的条件下,请说明哪种方案的总费用最少?
如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使,
连结DE、CF,连接BD交CF于点P.
求证:四边形CEDF是平行四边形;
若,求的周长.
(3)在(2)的条件下,求的面积.
四、综合题(每小题10分,共20分)
25.(10分)若实数m,n满足且时,就称点P为“完美点”。
(1)判断点A(2,3)、B(3,2)是不是完美点;
(2)若反比例函数的图像上存在两个“完美点”C、D,且CD=,请求出的值;
(3)已知抛物线上存在唯一的“完美点”,且当时,的最小值为,求值.
26.(10分)已知:O是坐标原点,P(m,n)(m>0)是函数上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(,0)(>m).设△OPA的面积为s,且.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求的值;
(3)若为小于20的整数,且,求OP2的最小值.
麓山国际实验学校2015—2016—2初三第六次限时训练
数 学 试 卷 答 案
选择题 ADACB BCDBA CD
填空题
14、 15、1 16、2:5 17、100 18、16
解答题
原式= (对一个点计1分,结果2分)………………6分
由(1)得 …………2分 由(2)得, …………4分
因为为正整数,所以=1或2
(1)200 (2)54 (3)50 (4) …………8分(每空两分)
(1)略 ……4分 (2) …………8分
(1)D地90,E地50;………………3分
(2)解得 为整数,或22 …………5分
方案一:A往D地21,往E地29;C往D地39,往E地11;
方案二:A往D地22,往E地28;C往D地38,往E地12.………6分
(3)方案一费用=元
方案二费用=元 ………………8分
所以方案一费用最少。 ………………9分
24、(1)在平行四边形ABCD中,AD∥BC 且 AD=BC, F为AC中点
,又,DF∥EC且DF=EC
四边形CEDF为平行四边形 ………………3分
(2)过D作,在平行四边形ABCD中,
在平行四边形CEDF中,
的周长= ………………6分
(3)过P作,PC∥DE,易得∽,
………9分
25、(1)A不是…………1分 B是 …………3分
(2),
即“完美点”P在直线上,设点C、D坐标分别为
令化简得
由韦达定理
解得,此时, ………………6分
(3)令,由于“完美点”唯一此方程
即 ………………7分
当时,的最小值为
若,则 此时无解;
若,则,解得 ………………8分
若,则 ,解得,(舍) …………9分
综上 ……………………10分
26、解:过点P作PQ⊥x轴于Q,则PQ=n,OQ=m,
(1)当n=1时,s=,(1分) ∴==.(3分)
(2)∵OP=AP,PA⊥OP,∴△OPA是等腰直角三角形.(4分)
∴m=n= ∴1+= . 即n4﹣4n2+4=0,∴k2﹣4k+4=0, ∴k=2.(6分)
(3)由=,整理得
∵PA⊥OP,作PQ⊥OA于Q,∴△OPQ∽△OAP.
由射影定理得: ,由勾股定理得,
化简得:2n4+2k2﹣kn4﹣4k=0 即(k﹣2)(2k﹣n4)=0,
∴k=2或k=
………8分
∵= 且n是大于0且小于20的整数,
当n=1时,OP2=5,
当n=2时,OP2=5,
当n=3时,OP2=32+
当n是大于3且小于20的整数时,显然有
∴OP2的最小值是5.(10分)
·A
B
C
O
y
x
第11题图
D
C
D
A
B
E
第12题图
C
B
F
A
E
18题
图①
球类
40%
跳绳
其它
踢毽15%
100
90
80
70
60
50
40
30
20
10
0
球类
跳绳
踢毽
其它
类别
30
40
80
人数
图②
数 学 试 卷
总 分:120分 时 量 :120分钟
一.选择题(3×12分=36分)
1、下列四个实数中是无理数的是( )
A.π B. C. D.0
2、下列图形中,是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3、已知空气的单位体积质量为克/厘米3,用小数表示为( )
A.0.00129 B.0.0129 C.-0.00129 D.0.000129
4、下列计算正确的是( )
A. B. C. D.
5、点P(4,﹣3)到轴的距离是( )
A.4 B.3 C.﹣3 D.5
6、我区某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )
班级 1班 2班 3班 4班 5班 6班
人数 52 60 62 54 58 62
A. 平均数是60 B. 中位数是59 C. 极差是40 D. 众数是58
7、抛物线的顶点坐标为( )
A.(1,-3) B.(-1,3) C.(-1,-3) D. (1,3)
8、若关于的一元二次方程有两个实数根,则的取值范围是( )
A. B. C. D. 且
9、为了控制房价,最近很多城市出台了房产购买限制措施,假设某人购买某处房子原来需支付首付款30%,即27万元,现在按照新规定首付款必须不低于50%,则这个人按照新规定至少支付首付款( )
A.13.5万元 B.45万元 C.54万元 D.100万元
10、一副三角板有两个直角三角形,如图叠放在一起,则∠的度数是( )
A.165° B.120° C.150° D.135°
11、如图,在平面直角坐标系中,点A在第一象限,⊙A与轴相切于B,与轴交于C(0,1)、D(0,4)两点,则点A的坐标是 ( )
A. B. C. D.
12、如图,将矩形ABCD沿对角线折叠,使落在处,交于,则下列结论不一定成立的是( )
A. B. C. D.
第10题图
二 、填空题(3分×6=18分)
13、分解因式:= .
14、若是方程的解,则的值为
15、已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为,则a等于
16、如图,△ABC中,DE∥BC,AE:EB=2:3,则DE:BC= .
17、某水库堤坝的横断面如图,迎水坡AB的坡度是1:,堤坝高BC=50m,则AB= m.
18、如图,在Rt△ABC中,,AB=AC=,点E为AC的中点,点F在底边BC上,且,则△的面积为
16题 17题
三、解答题(6小题,共46分)
19、(6分)计算:﹣3tan30°+(π﹣4)0+
20、(6分)解不等式组,并写出不等式的正整数解。
21.(8分)某校为了进一步丰富学生的课外体育活动,欲增购一些体育器材,为此该校对一部分学生进行了一次题为“你最喜欢的体育活动”的问卷调查(每人只选一项).
根据收集到的数据,绘制成如下统计图(不完整):
请根据图中提供的信息,完成下列问题:
(1)在这次问卷调查中,一共抽查了 名学生;
(2)图①中,“踢毽”部分所对应的圆心角为 度;
(3)“跳绳”部分的学生有 人;
(4)如果全校有1 860名学生, 从中调查一名学生,
这个学生最喜欢的体育活动是跳绳的概率是多少?
22、如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=,求⊙O的直径。
23.(9分)在长沙市开展城乡综合治理的活动中,需要将A、B、C三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场D、E两地进行处理.已知运往D地的数量比运往E地的数量的2倍少10立方米,
(1)求运往D、E两地的数量各是多少立方米?
(2)若A地运往D地a立方米(a为整数),B地运往D地30立方米,C地运往D地的数量小于A地运往D地的2倍,其余全部运往E地,且C地运往E地不超过12立方米,则A、C两地运往D、E两地有哪几种方案?
(3)已知从A、B、C三地把垃圾运往D、E两地处理所需费用如下表:
A地 B地 C地
运往D地(元/立方米) 22 20 20
运往E地(元/立方米) 20 22 21
在(2)的条件下,请说明哪种方案的总费用最少?
如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使,
连结DE、CF,连接BD交CF于点P.
求证:四边形CEDF是平行四边形;
若,求的周长.
(3)在(2)的条件下,求的面积.
四、综合题(每小题10分,共20分)
25.(10分)若实数m,n满足且时,就称点P为“完美点”。
(1)判断点A(2,3)、B(3,2)是不是完美点;
(2)若反比例函数的图像上存在两个“完美点”C、D,且CD=,请求出的值;
(3)已知抛物线上存在唯一的“完美点”,且当时,的最小值为,求值.
26.(10分)已知:O是坐标原点,P(m,n)(m>0)是函数上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(,0)(>m).设△OPA的面积为s,且.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求的值;
(3)若为小于20的整数,且,求OP2的最小值.
麓山国际实验学校2015—2016—2初三第六次限时训练
数 学 试 卷 答 案
选择题 ADACB BCDBA CD
填空题
14、 15、1 16、2:5 17、100 18、16
解答题
原式= (对一个点计1分,结果2分)………………6分
由(1)得 …………2分 由(2)得, …………4分
因为为正整数,所以=1或2
(1)200 (2)54 (3)50 (4) …………8分(每空两分)
(1)略 ……4分 (2) …………8分
(1)D地90,E地50;………………3分
(2)解得 为整数,或22 …………5分
方案一:A往D地21,往E地29;C往D地39,往E地11;
方案二:A往D地22,往E地28;C往D地38,往E地12.………6分
(3)方案一费用=元
方案二费用=元 ………………8分
所以方案一费用最少。 ………………9分
24、(1)在平行四边形ABCD中,AD∥BC 且 AD=BC, F为AC中点
,又,DF∥EC且DF=EC
四边形CEDF为平行四边形 ………………3分
(2)过D作,在平行四边形ABCD中,
在平行四边形CEDF中,
的周长= ………………6分
(3)过P作,PC∥DE,易得∽,
………9分
25、(1)A不是…………1分 B是 …………3分
(2),
即“完美点”P在直线上,设点C、D坐标分别为
令化简得
由韦达定理
解得,此时, ………………6分
(3)令,由于“完美点”唯一此方程
即 ………………7分
当时,的最小值为
若,则 此时无解;
若,则,解得 ………………8分
若,则 ,解得,(舍) …………9分
综上 ……………………10分
26、解:过点P作PQ⊥x轴于Q,则PQ=n,OQ=m,
(1)当n=1时,s=,(1分) ∴==.(3分)
(2)∵OP=AP,PA⊥OP,∴△OPA是等腰直角三角形.(4分)
∴m=n= ∴1+= . 即n4﹣4n2+4=0,∴k2﹣4k+4=0, ∴k=2.(6分)
(3)由=,整理得
∵PA⊥OP,作PQ⊥OA于Q,∴△OPQ∽△OAP.
由射影定理得: ,由勾股定理得,
化简得:2n4+2k2﹣kn4﹣4k=0 即(k﹣2)(2k﹣n4)=0,
∴k=2或k=
………8分
∵= 且n是大于0且小于20的整数,
当n=1时,OP2=5,
当n=2时,OP2=5,
当n=3时,OP2=32+
当n是大于3且小于20的整数时,显然有
∴OP2的最小值是5.(10分)
·A
B
C
O
y
x
第11题图
D
C
D
A
B
E
第12题图
C
B
F
A
E
18题
图①
球类
40%
跳绳
其它
踢毽15%
100
90
80
70
60
50
40
30
20
10
0
球类
跳绳
踢毽
其它
类别
30
40
80
人数
图②
同课章节目录
