八年级数学下册试题 18.1.1 平行四边形的性质同步测试(含答案)
文档属性
| 名称 | 八年级数学下册试题 18.1.1 平行四边形的性质同步测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 785.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 15:19:02 | ||
图片预览



文档简介
18.1.1 平行四边形的性质
一、单选题:
1.下列说法不正确的是( )
A.平行四边形两组对边分别平行 B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等 D.平行四边形的两组对边分别相等
2.如图,平行四边形ABCD的周长为,的周长为,则对角线的长为( )
A. B. C. D.
3.如图,平行四边形ABCD的对角线与相交于点O,.若,,则的长是( )
A.10 B.8 C.12 D.14
4.平行四边形ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则边AB长的取值范围是( )
A.3≤AB≤4 B.2<AB<14 C.1<AB<7 D.1≤AB≤7
5.如图,O为平行四边形ABCD对角线的交点,,交边于点E,连接.若的周长比的周长大8,则的长有可能为( )
A.2 B.3 C.4 D.5
6.如图,已知平行四边形的面积为48,E为的中点,连接,则的面积为( )
A.8 B.6 C.4 D.3
7.如图,在平行四边形OABC中,对角线相交于点E,OA边在x轴上,点O为坐标原点,已知点A(4,0),E(3,1),则点C的坐标为( )
A. B. C. D.
二、填空题:
8.在平行四边形中一边长为,它的一条对角线的长,那么它的另一条对角线的长度的取值范围______.
9.如图,在平行四边形ABCD中,点O是对角线的交点,垂直于,且 ,则______.
10.如图,平行四边形ABCD的对角线,相交于,已知,且的周长比的周长大1,则平行四边形ABCD的周长等于__________.
11.如图,平行四边形的对角线与相交于点,,垂足为,,,,则的长为______.
12.如图,平行四边形ABCD中,对角线交于点O,直线MN经过点O,分别交AD,BC于点M,N,若∠MDO=∠MOD,BN=2.则MN的长为________.
13.如图,平行四边形ABCD 中,,,,对角线,交于点O,过点O作,则等于______.
14.如图,在平行四边形中,对角线的垂直平分线分别交、于点E、F,连接,若的周长为6,则四边形的周长为___________.
三、解答题:
15.在 ABCD中,AC、BD交于点O.过点O作OE⊥BD交BC于点E,连接DE.若∠CDE=∠CBD=15°.求∠ABC的度数.
16.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为点E,F,求证:AC,EF互相平分.
17.已知:如图,在平行四边形ABCD中,过的中点O的直线分别交,的延长线于点E,F.
求证:.
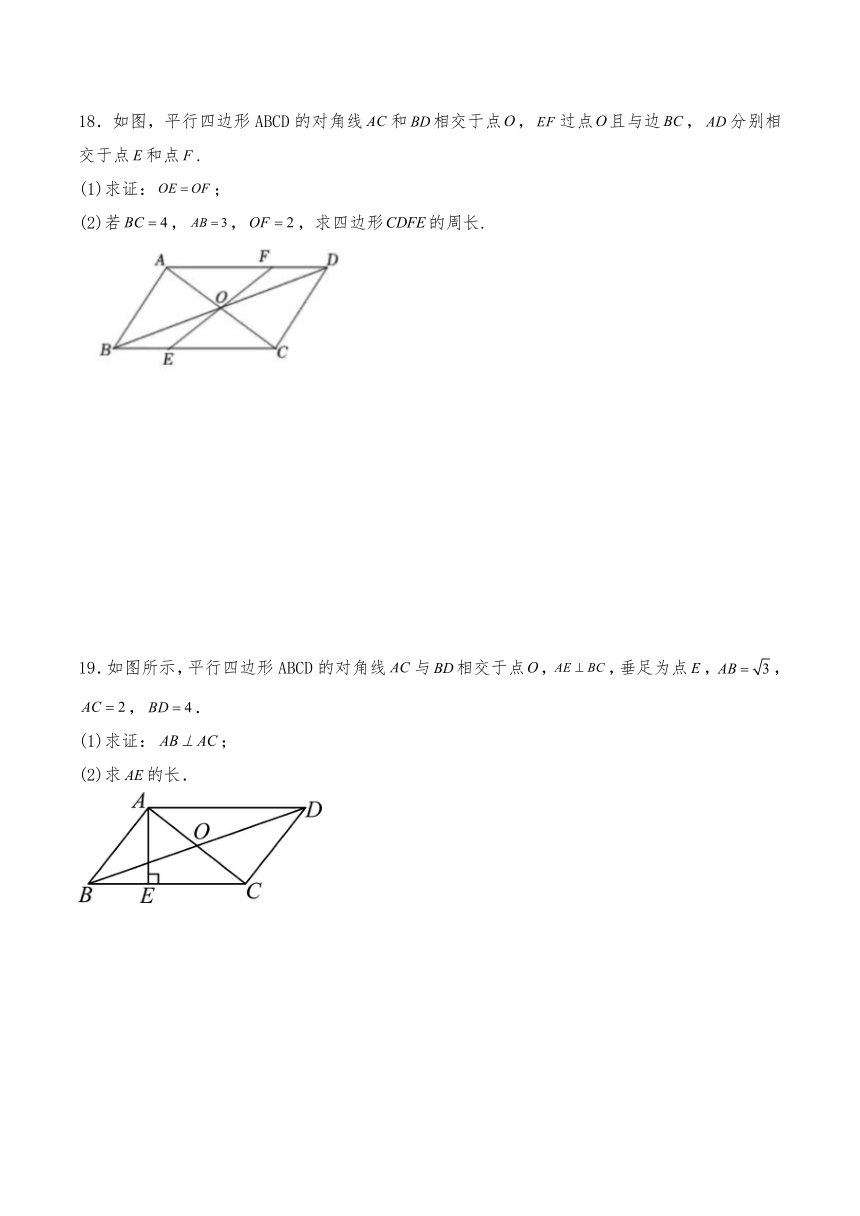
18.如图,平行四边形ABCD的对角线和相交于点,过点且与边,分别相交于点和点.
(1)求证:;
(2)若,,,求四边形的周长.
19.如图所示,平行四边形ABCD的对角线与相交于点,,垂足为点,,,.
(1)求证:;
(2)求的长.
20.已知平行四边形ABCD中,对角线AC、BD相交于点O,AB=AC,AB⊥AC.
(1)如图1,若,求AB的长;
(2)如图2,过点C作CE⊥BD于点E,连接AE,过点A作AF⊥AE交BD于点F,求证:OF=CE+OE.
答案
一、单选题:
1.C
【分析】根据平行四边形的性质依次分析判断即可.
【详解】解:A.平行四边形两组对边分别平行,原说法正确,故该项不符合题意;
B.平行四边形的对角线互相平分,原说法正确,故该项不符合题意;
C.平行四边形的对角相等,邻角互补,原说法不正确,故该项符合题意;
D.平行四边形的两组对边分别相等,原说法正确,故该项不符合题意;
故选:C.
2.C
【分析】因为平行四边形对边相等,所以平行四边形的周长为相邻两边之和的倍,即,则,而的周长,即可求出的长.
【详解】∵平行四边形ABCD的周长是,
∴
∴,
∵的周长是,
∴,
∴.
故选:C.
3.A
【分析】根据平行四边形的性质可得,,根据勾股定理可求出的长,从而可得的长.
【详解】解:∵四边形是平行四边形,
∴,
∵,
∴,
∴.
故选:A.
4.C
【分析】利用平行四边形的对角线互相平分和三角形的三边关系进行求解即可.
【详解】解:∵四边形ABCD是平行四边形,
∴AO=AC,BO=BD,
∵AC=8,BD=6,
∴AO=4,BO=3,
∴4﹣3<AB<4+3,
解得1<AB<7.
故选C.
5.D
【分析】依据平行四边形的性质以及线段垂直平分线的性质,即可得到的长,再根据,即可得出结论.
【详解】解:∵四边形是平行四边形,
∴,O是的中点,
又∵,
∴垂直平分,
∴,
∴,
∵的周长比的周长大8,
∴,
即,
∴,则,
又∵中,,
∴,
观察四个选项,的长可能为5,
故选:D.
6.B
【分析】根据平行四边形的性质得出O为的中点,利用三角形中线将原三角形分成两个面积相等的三角形求解即可.
【详解】解:四边形为平行四边形,
O为、的中点,,
E为的中点,
,
O为的中点,
,
故选B.
7.C
【分析】由平行四边形的性质得AE=CE,即点E是AC的中点,设C(a,b),利用中点坐标公式,进而求解C点坐标.
【详解】解:设C(a,b),
∵四边形ABCO为平行四边形,
∴AE=CE,即点E是AC的中点,
∵A(4,0),E(3,1),
∴=3,=1,
解得:a=2,b=2,
∴C(2,2).
故选:C.
二、填空题:
8.
【分析】根据平行四边形性质推出,,在中,由三角形三边关系定理得出,求出即可.
【详解】解:∵四边形是平行四边形,
∴,,
在中,,由三角形三边关系定理得:,
即,
.
故答案为:.
9.
【分析】先利用平行四边形的性质得到cm,cm,然后在中,利用勾股定理求得.
【详解】∵四边形是平行四边形,cm,
∴cm,cm,
∵垂直于,
∴,
∴在中,cm,
故答案为:
10.10
【分析】根据平行四边形的性质可知,平行四边形的对角线互相平分,由于△ADO的周长比△ABO的周长大1,则AD比AB大1,所以可以求出AD,进而求出周长.
【详解】解:∵四边形ABCD为平行四边形,
∴BO=DO,AB=CD,AD=BC,
∵△ADO的周长比△ABO的周长大1,
∴AD﹣AB=1,
∵AB=2,
∴AD=3,
∴AB+AD=5,
∴平行四边形的周长为.
故答案为:10.
11.
【分析】首先由勾股定理的逆定理判定是直角三角形,再利用三角形的面积公式即可求出的长度.
【详解】解:四边形是平行四边形,,,
,,
,
,
,
在中,,,
,
,
故答案为:.
12.
【分析】先证明,得出,,根据,得出,再等量代换得到,根据求出的长即可.
【详解】解:∵在平行四边形ABCD中,
∴,,
∴,
又∵(对顶角相等),
∴,
∴,,
又∵,
∴CM=DM=2,
∴,
∴,
故答案为:.
13.
【分析】过点C作于F,先根据直角三角形的性质与勾股定理求出,然后利用的面积等于平行四边形ABCD面积的,从而得解.
【详解】解:过点C作于F,如图所示,
,
,,
,
,
,
,
,
;
故答案为:.
14.12
【分析】由平行四边形的性质得出,,由线段垂直平分线的性质得出,得出的周长,即可得出结果.
【详解】解:∵四边形是平行四边形,
∴,,
∵的垂直平分线交于点E,
∴,
∴的周长,
∴四边形的周长;
故答案为:12.
三、解答题:
15.解:∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE⊥BD,
∴BE=ED,
∴,
∵,
∴,
∵四边形ABCD是平行四边形,
∴,
∴,
∴.
16.证明:∵四边形ABCD是平行四边形,
∴AO=CO.
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°.
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴OE=OF,
AC,EF互相平分.
17.证明:∵四边形是平行四边形,
∴,,,
在和中,
∴,
∴,
∵,
∴,
即.
18.(1)证明:∵四边形是平行四边形,
∴,,
∴,
∵在和中,
∴,
∴.
(2)解:∵,
∴,
∵四边形是平行四边形,
∴,,
∵,,,
∴
.
19.(1)
证明:∵四边形ABCD为平行四边形,,,
∴OA = AC = 1,OB = BD = 2.
又∵AB = ,
∴OA2 + AB2 = OB2,
∴△BAO为直角三角形,且∠BAO = 90°,
∴;
(2)
解:∵△BAC为直角三角形,且∠BAC = 90°,
∴,
∵,,
∴,,
∴,
∴.
20.(1)
解:在平行四边形ABCD中,,
∵,
∴,
设则,
∵AB⊥AC,
∴,即,
解得:;
∴
(2)
过点C作CG//AF,交BD于点G,
∴∠FAC=∠OCG,∠AFO=∠OGC,
∵OA=OC,
∴,
∴OF=OG,
∵AB⊥AC,AF⊥AE,
∴∠BAC=∠FAE=90°,
∴∠BAC-∠FAO=∠FAE-∠FAO,
∴∠BAF=∠CAE,
∵CE⊥BD,
∴∠CED=∠CEF=90°,
∴∠AEC=∠AEF+∠CEF=90°+∠AEF,
∵∠AFB是的一个外角,
∴∠AFB=∠FAE+∠AEF=90°+∠AEF,
∴∠AEC=∠AFB,
∵AB=AC,
∴∠AFE=∠AEF=45°,
∴∠AFE=∠CGO=45°,
∴是等腰直角三角形,
∴CE=EG,
∵OG=OE+EG,
∴OF=OE+CE.
一、单选题:
1.下列说法不正确的是( )
A.平行四边形两组对边分别平行 B.平行四边形的对角线互相平分
C.平行四边形的对角互补,邻角相等 D.平行四边形的两组对边分别相等
2.如图,平行四边形ABCD的周长为,的周长为,则对角线的长为( )
A. B. C. D.
3.如图,平行四边形ABCD的对角线与相交于点O,.若,,则的长是( )
A.10 B.8 C.12 D.14
4.平行四边形ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则边AB长的取值范围是( )
A.3≤AB≤4 B.2<AB<14 C.1<AB<7 D.1≤AB≤7
5.如图,O为平行四边形ABCD对角线的交点,,交边于点E,连接.若的周长比的周长大8,则的长有可能为( )
A.2 B.3 C.4 D.5
6.如图,已知平行四边形的面积为48,E为的中点,连接,则的面积为( )
A.8 B.6 C.4 D.3
7.如图,在平行四边形OABC中,对角线相交于点E,OA边在x轴上,点O为坐标原点,已知点A(4,0),E(3,1),则点C的坐标为( )
A. B. C. D.
二、填空题:
8.在平行四边形中一边长为,它的一条对角线的长,那么它的另一条对角线的长度的取值范围______.
9.如图,在平行四边形ABCD中,点O是对角线的交点,垂直于,且 ,则______.
10.如图,平行四边形ABCD的对角线,相交于,已知,且的周长比的周长大1,则平行四边形ABCD的周长等于__________.
11.如图,平行四边形的对角线与相交于点,,垂足为,,,,则的长为______.
12.如图,平行四边形ABCD中,对角线交于点O,直线MN经过点O,分别交AD,BC于点M,N,若∠MDO=∠MOD,BN=2.则MN的长为________.
13.如图,平行四边形ABCD 中,,,,对角线,交于点O,过点O作,则等于______.
14.如图,在平行四边形中,对角线的垂直平分线分别交、于点E、F,连接,若的周长为6,则四边形的周长为___________.
三、解答题:
15.在 ABCD中,AC、BD交于点O.过点O作OE⊥BD交BC于点E,连接DE.若∠CDE=∠CBD=15°.求∠ABC的度数.
16.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为点E,F,求证:AC,EF互相平分.
17.已知:如图,在平行四边形ABCD中,过的中点O的直线分别交,的延长线于点E,F.
求证:.
18.如图,平行四边形ABCD的对角线和相交于点,过点且与边,分别相交于点和点.
(1)求证:;
(2)若,,,求四边形的周长.
19.如图所示,平行四边形ABCD的对角线与相交于点,,垂足为点,,,.
(1)求证:;
(2)求的长.
20.已知平行四边形ABCD中,对角线AC、BD相交于点O,AB=AC,AB⊥AC.
(1)如图1,若,求AB的长;
(2)如图2,过点C作CE⊥BD于点E,连接AE,过点A作AF⊥AE交BD于点F,求证:OF=CE+OE.
答案
一、单选题:
1.C
【分析】根据平行四边形的性质依次分析判断即可.
【详解】解:A.平行四边形两组对边分别平行,原说法正确,故该项不符合题意;
B.平行四边形的对角线互相平分,原说法正确,故该项不符合题意;
C.平行四边形的对角相等,邻角互补,原说法不正确,故该项符合题意;
D.平行四边形的两组对边分别相等,原说法正确,故该项不符合题意;
故选:C.
2.C
【分析】因为平行四边形对边相等,所以平行四边形的周长为相邻两边之和的倍,即,则,而的周长,即可求出的长.
【详解】∵平行四边形ABCD的周长是,
∴
∴,
∵的周长是,
∴,
∴.
故选:C.
3.A
【分析】根据平行四边形的性质可得,,根据勾股定理可求出的长,从而可得的长.
【详解】解:∵四边形是平行四边形,
∴,
∵,
∴,
∴.
故选:A.
4.C
【分析】利用平行四边形的对角线互相平分和三角形的三边关系进行求解即可.
【详解】解:∵四边形ABCD是平行四边形,
∴AO=AC,BO=BD,
∵AC=8,BD=6,
∴AO=4,BO=3,
∴4﹣3<AB<4+3,
解得1<AB<7.
故选C.
5.D
【分析】依据平行四边形的性质以及线段垂直平分线的性质,即可得到的长,再根据,即可得出结论.
【详解】解:∵四边形是平行四边形,
∴,O是的中点,
又∵,
∴垂直平分,
∴,
∴,
∵的周长比的周长大8,
∴,
即,
∴,则,
又∵中,,
∴,
观察四个选项,的长可能为5,
故选:D.
6.B
【分析】根据平行四边形的性质得出O为的中点,利用三角形中线将原三角形分成两个面积相等的三角形求解即可.
【详解】解:四边形为平行四边形,
O为、的中点,,
E为的中点,
,
O为的中点,
,
故选B.
7.C
【分析】由平行四边形的性质得AE=CE,即点E是AC的中点,设C(a,b),利用中点坐标公式,进而求解C点坐标.
【详解】解:设C(a,b),
∵四边形ABCO为平行四边形,
∴AE=CE,即点E是AC的中点,
∵A(4,0),E(3,1),
∴=3,=1,
解得:a=2,b=2,
∴C(2,2).
故选:C.
二、填空题:
8.
【分析】根据平行四边形性质推出,,在中,由三角形三边关系定理得出,求出即可.
【详解】解:∵四边形是平行四边形,
∴,,
在中,,由三角形三边关系定理得:,
即,
.
故答案为:.
9.
【分析】先利用平行四边形的性质得到cm,cm,然后在中,利用勾股定理求得.
【详解】∵四边形是平行四边形,cm,
∴cm,cm,
∵垂直于,
∴,
∴在中,cm,
故答案为:
10.10
【分析】根据平行四边形的性质可知,平行四边形的对角线互相平分,由于△ADO的周长比△ABO的周长大1,则AD比AB大1,所以可以求出AD,进而求出周长.
【详解】解:∵四边形ABCD为平行四边形,
∴BO=DO,AB=CD,AD=BC,
∵△ADO的周长比△ABO的周长大1,
∴AD﹣AB=1,
∵AB=2,
∴AD=3,
∴AB+AD=5,
∴平行四边形的周长为.
故答案为:10.
11.
【分析】首先由勾股定理的逆定理判定是直角三角形,再利用三角形的面积公式即可求出的长度.
【详解】解:四边形是平行四边形,,,
,,
,
,
,
在中,,,
,
,
故答案为:.
12.
【分析】先证明,得出,,根据,得出,再等量代换得到,根据求出的长即可.
【详解】解:∵在平行四边形ABCD中,
∴,,
∴,
又∵(对顶角相等),
∴,
∴,,
又∵,
∴CM=DM=2,
∴,
∴,
故答案为:.
13.
【分析】过点C作于F,先根据直角三角形的性质与勾股定理求出,然后利用的面积等于平行四边形ABCD面积的,从而得解.
【详解】解:过点C作于F,如图所示,
,
,,
,
,
,
,
,
;
故答案为:.
14.12
【分析】由平行四边形的性质得出,,由线段垂直平分线的性质得出,得出的周长,即可得出结果.
【详解】解:∵四边形是平行四边形,
∴,,
∵的垂直平分线交于点E,
∴,
∴的周长,
∴四边形的周长;
故答案为:12.
三、解答题:
15.解:∵四边形ABCD是平行四边形,
∴OB=OD,
∵OE⊥BD,
∴BE=ED,
∴,
∵,
∴,
∵四边形ABCD是平行四边形,
∴,
∴,
∴.
16.证明:∵四边形ABCD是平行四边形,
∴AO=CO.
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°.
在△AEO和△CFO中,
,
∴△AEO≌△CFO(AAS),
∴OE=OF,
AC,EF互相平分.
17.证明:∵四边形是平行四边形,
∴,,,
在和中,
∴,
∴,
∵,
∴,
即.
18.(1)证明:∵四边形是平行四边形,
∴,,
∴,
∵在和中,
∴,
∴.
(2)解:∵,
∴,
∵四边形是平行四边形,
∴,,
∵,,,
∴
.
19.(1)
证明:∵四边形ABCD为平行四边形,,,
∴OA = AC = 1,OB = BD = 2.
又∵AB = ,
∴OA2 + AB2 = OB2,
∴△BAO为直角三角形,且∠BAO = 90°,
∴;
(2)
解:∵△BAC为直角三角形,且∠BAC = 90°,
∴,
∵,,
∴,,
∴,
∴.
20.(1)
解:在平行四边形ABCD中,,
∵,
∴,
设则,
∵AB⊥AC,
∴,即,
解得:;
∴
(2)
过点C作CG//AF,交BD于点G,
∴∠FAC=∠OCG,∠AFO=∠OGC,
∵OA=OC,
∴,
∴OF=OG,
∵AB⊥AC,AF⊥AE,
∴∠BAC=∠FAE=90°,
∴∠BAC-∠FAO=∠FAE-∠FAO,
∴∠BAF=∠CAE,
∵CE⊥BD,
∴∠CED=∠CEF=90°,
∴∠AEC=∠AEF+∠CEF=90°+∠AEF,
∵∠AFB是的一个外角,
∴∠AFB=∠FAE+∠AEF=90°+∠AEF,
∴∠AEC=∠AFB,
∵AB=AC,
∴∠AFE=∠AEF=45°,
∴∠AFE=∠CGO=45°,
∴是等腰直角三角形,
∴CE=EG,
∵OG=OE+EG,
∴OF=OE+CE.
