湘教版数学八年级下册第一次月考试题(含答案)
文档属性
| 名称 | 湘教版数学八年级下册第一次月考试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 602.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版数学八年级下册第一次月考试题
一、填空题
1.将一副三角尺如图所示叠放在一起,若AB=4cm,则阴影部分的面积是 cm2.
2.如图,已知直线,相交于点,如果,平分,那么 度.
3.如图,已知AB∥CD,E、F、H分别为AB、CD、AC上一点(∠DFK<∠BEK),KG平分∠EKF,∠AEK+∠HKE=180°.则下列结论:①CD∥KH;②∠BEK+∠DFK=2∠EKG;③∠BEK-∠DFK=∠GKH;④∠BAC+∠AGK-∠GKF+∠DFK=180°.其中正确的是 .(填序号)
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC=4,点D在线段BC上,BD=3,将线段AD绕点A逆时针旋转90°得到线段AE,EF⊥AC,垂足为点F.则AF的长为 .
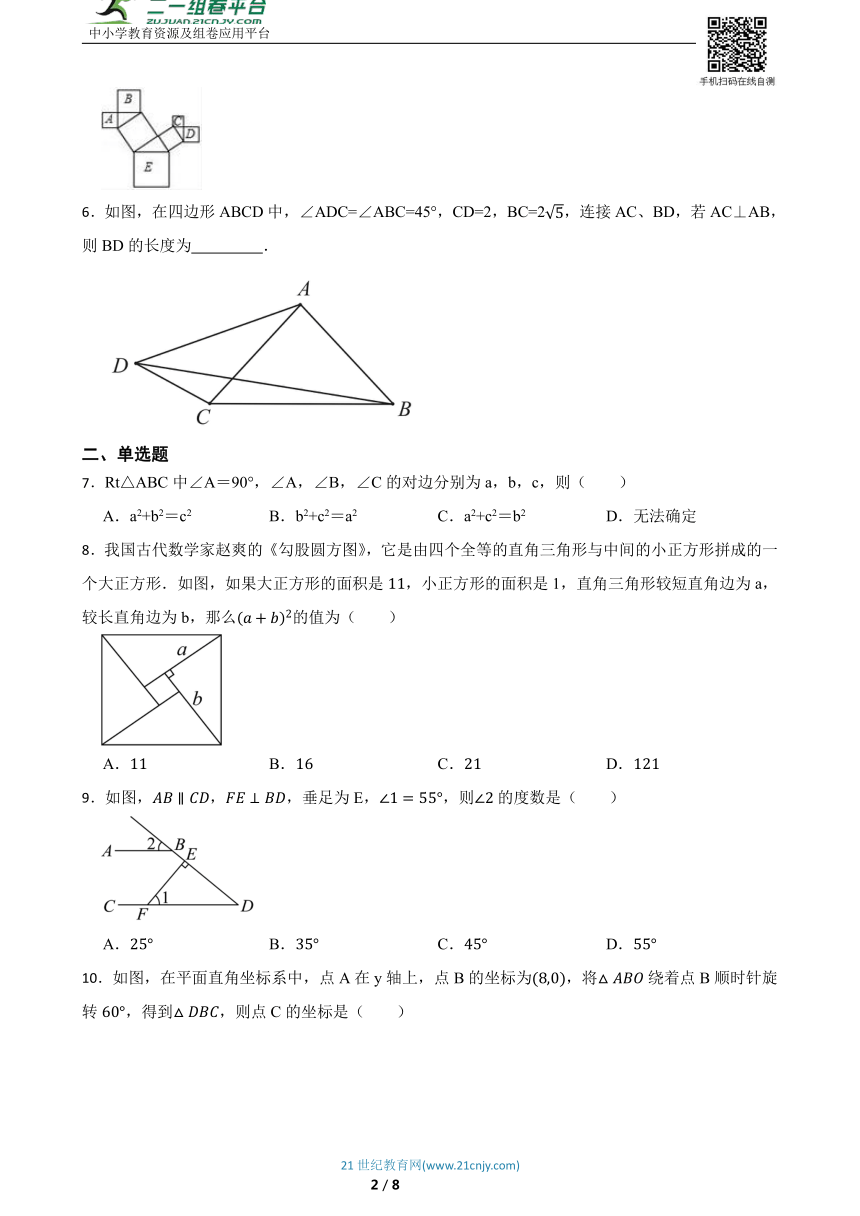
5.如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,已知正方形A,B,C,D的边长分别是6,8,3,4,则最大正方形E的面积是 .
6.如图,在四边形ABCD中,∠ADC=∠ABC=45°,CD=2,BC=2,连接AC、BD,若AC⊥AB,则BD的长度为 .
二、单选题
7.Rt△ABC中∠A=90°,∠A,∠B,∠C的对边分别为a,b,c,则( )
A.a2+b2=c2 B.b2+c2=a2 C.a2+c2=b2 D.无法确定
8.我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如图,如果大正方形的面积是,小正方形的面积是1,直角三角形较短直角边为a,较长直角边为b,那么的值为( )
A. B. C. D.
9.如图,,,垂足为E,,则的度数是( )
A. B. C. D.
10.如图,在平面直角坐标系中,点A在y轴上,点B的坐标为,将绕着点B顺时针旋转,得到,则点C的坐标是( )
A. B. C. D.
11.一个长方体盒子长,宽,在这个盒子中水平放置一根木棒,那么这根木棒最长(不计木棒粗细)可以是( )
A. B. C. D.
12.如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,分别以AC,BC,AB为一边在△ABC外面做三个正方形,记三个正方形的面积依次为,,.已知,则为( )
A.18 B.27 C.36 D.45
13.一个直角三角形的两直角边长分别为3,4,则第三边长是( )
A.3 B.4 C.5 D.6
14.若a,b是Rt△ABC的两直角边长,若 ,△ABC的面积24,则斜边c为( )
A.5 B.10 C.15 D.20
15.如图,将三角板绕点逆时针旋转一定角度,过点在三角板的内部作射线,使得恰好是的角平分线,此时与满足的数量关系是( )
A. B.
C. D.
16.如图,E在线段的延长线上,,连交于G,的余角比大,K为线段上一点,连,使,在内部有射线,平分.则下列结论:①;②平分;③;④.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
三、解答题
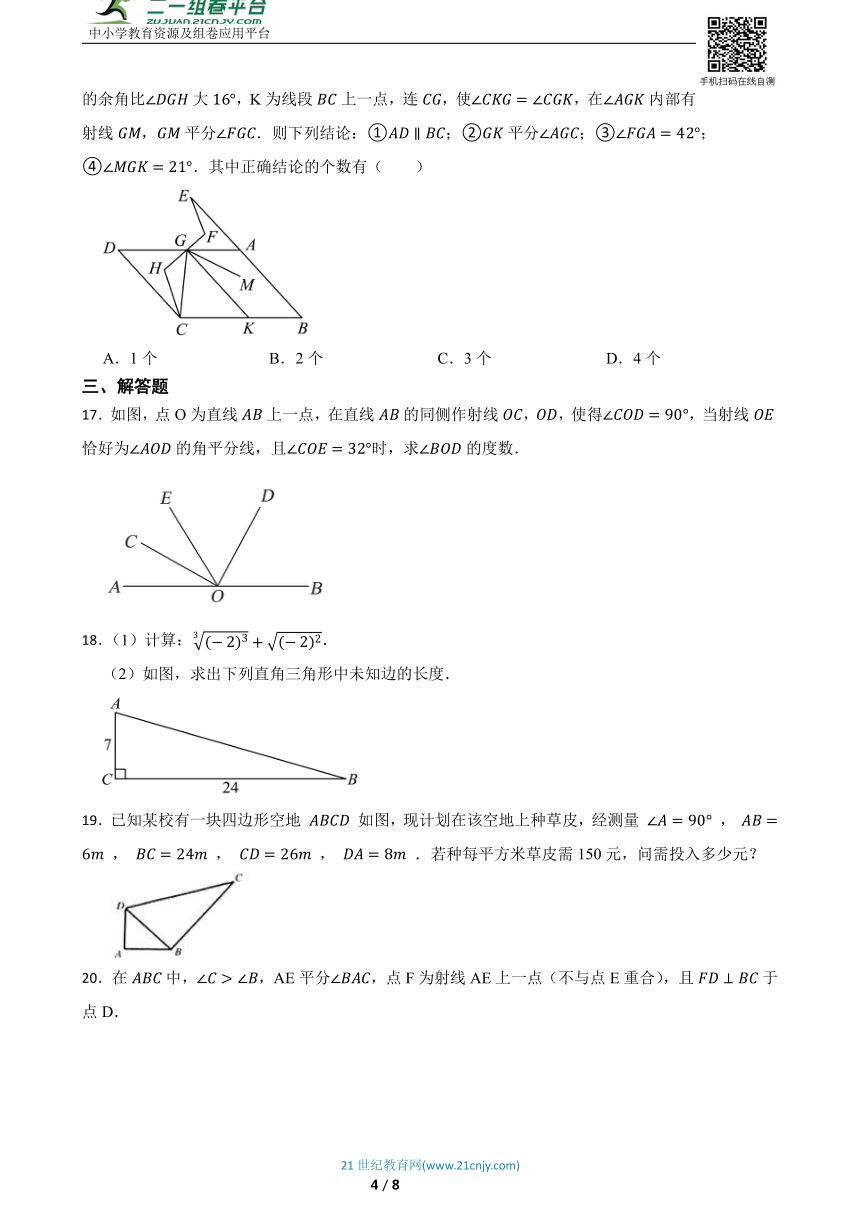
17.如图,点O为直线上一点,在直线的同侧作射线,,使得,当射线恰好为的角平分线,且时,求的度数.
18.(1)计算:.
(2)如图,求出下列直角三角形中未知边的长度.
19.已知某校有一块四边形空地 如图,现计划在该空地上种草皮,经测量 , , , , .若种每平方米草皮需150元,问需投入多少元?
20.在中,,AE平分,点F为射线AE上一点(不与点E重合),且于点D.
(1)如图1,如果点F在线段AE上,且,,则_______°;
(2)如果点F在的外部,分别作出和的角平分线,交于点K,请在图2中补全图形,探究、、三者之间的数量关系,并说明理由;
(3)如图3,若点F与点A重合,PE、PC分别平分和的外角,连接PA,过点P作交BC延长线于点G,交BA的延长线于点H,若,且,请直接写出与的度数.
四、计算题
21.如图,在中,,于点,,求的长.
22.点为直线上一点,在直线同侧任作射线,,使得.
(1)如图一,过点作射线,使为的角平分线,若时,则=______°.
(2)如图二,过点作射线,当恰好为的角平分线时,另作射线,使得平分.
①若,求的度数(写出推理过程).
②若,则的度数是______(直接填空).
(3)过点作射线,当恰好为的角平分线时,另作射线,使得平分,当时,则的度数是______.(直接填空)
23.如图,C为线段上一动点,分别过点B,D作,连接.已知.
(1)求当x等于何值时,
(2)当时,求的长.
(3)利用图形求代数式的最小值.
答案解析部分
1.【答案】2
【知识点】含30°角的直角三角形
2.【答案】40
【知识点】角平分线的性质;对顶角及其性质
3.【答案】①②④
【知识点】平行线的性质;平行线的判定与性质;角平分线的性质
4.【答案】1
【知识点】勾股定理;旋转的性质
5.【答案】125
【知识点】勾股定理
6.【答案】
【知识点】等腰三角形的判定与性质;勾股定理
7.【答案】B
【知识点】勾股定理
8.【答案】C
【知识点】完全平方公式的几何背景;勾股定理
9.【答案】B
【知识点】直角三角形的性质;同位角的概念
10.【答案】C
【知识点】含30°角的直角三角形;勾股定理;旋转的性质
11.【答案】C
【知识点】勾股定理
12.【答案】C
【知识点】含30°角的直角三角形;勾股定理
13.【答案】C
【知识点】勾股定理
14.【答案】B
【知识点】三角形的面积;勾股定理
15.【答案】B
【知识点】角的运算;余角、补角及其性质;角平分线的性质
16.【答案】B
【知识点】平行线的判定与性质;角平分线的性质;对顶角及其性质
17.【答案】
【知识点】角的运算;角平分线的性质
18.【答案】(1)0;(2)
【知识点】勾股定理;求算术平方根;开立方(求立方根)
19.【答案】解:∵ , , ,
∴ ,
∵ , ,∴ ,
∴ 是直角三角形,
∴ ,
∴需投入总资金为: (元).
【知识点】勾股定理;勾股定理的逆定理
20.【答案】(1);
(2);
(3),.
【知识点】垂线的概念;三角形内角和定理;三角形的外角性质;角平分线的性质
21.【答案】
【知识点】最简二次根式;垂线的概念;勾股定理
22.【答案】(1)
(2)①②
(3)或
【知识点】角的运算;余角、补角及其性质;角平分线的性质
23.【答案】(1)
(2)
(3)
【知识点】勾股定理
21世纪教育网(www.21cnjy.com)
1 / 8
湘教版数学八年级下册第一次月考试题
一、填空题
1.将一副三角尺如图所示叠放在一起,若AB=4cm,则阴影部分的面积是 cm2.
2.如图,已知直线,相交于点,如果,平分,那么 度.
3.如图,已知AB∥CD,E、F、H分别为AB、CD、AC上一点(∠DFK<∠BEK),KG平分∠EKF,∠AEK+∠HKE=180°.则下列结论:①CD∥KH;②∠BEK+∠DFK=2∠EKG;③∠BEK-∠DFK=∠GKH;④∠BAC+∠AGK-∠GKF+∠DFK=180°.其中正确的是 .(填序号)
4.如图,在Rt△ABC中,∠BAC=90°,AB=AC=4,点D在线段BC上,BD=3,将线段AD绕点A逆时针旋转90°得到线段AE,EF⊥AC,垂足为点F.则AF的长为 .
5.如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,已知正方形A,B,C,D的边长分别是6,8,3,4,则最大正方形E的面积是 .
6.如图,在四边形ABCD中,∠ADC=∠ABC=45°,CD=2,BC=2,连接AC、BD,若AC⊥AB,则BD的长度为 .
二、单选题
7.Rt△ABC中∠A=90°,∠A,∠B,∠C的对边分别为a,b,c,则( )
A.a2+b2=c2 B.b2+c2=a2 C.a2+c2=b2 D.无法确定
8.我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如图,如果大正方形的面积是,小正方形的面积是1,直角三角形较短直角边为a,较长直角边为b,那么的值为( )
A. B. C. D.
9.如图,,,垂足为E,,则的度数是( )
A. B. C. D.
10.如图,在平面直角坐标系中,点A在y轴上,点B的坐标为,将绕着点B顺时针旋转,得到,则点C的坐标是( )
A. B. C. D.
11.一个长方体盒子长,宽,在这个盒子中水平放置一根木棒,那么这根木棒最长(不计木棒粗细)可以是( )
A. B. C. D.
12.如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,分别以AC,BC,AB为一边在△ABC外面做三个正方形,记三个正方形的面积依次为,,.已知,则为( )
A.18 B.27 C.36 D.45
13.一个直角三角形的两直角边长分别为3,4,则第三边长是( )
A.3 B.4 C.5 D.6
14.若a,b是Rt△ABC的两直角边长,若 ,△ABC的面积24,则斜边c为( )
A.5 B.10 C.15 D.20
15.如图,将三角板绕点逆时针旋转一定角度,过点在三角板的内部作射线,使得恰好是的角平分线,此时与满足的数量关系是( )
A. B.
C. D.
16.如图,E在线段的延长线上,,连交于G,的余角比大,K为线段上一点,连,使,在内部有射线,平分.则下列结论:①;②平分;③;④.其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
三、解答题
17.如图,点O为直线上一点,在直线的同侧作射线,,使得,当射线恰好为的角平分线,且时,求的度数.
18.(1)计算:.
(2)如图,求出下列直角三角形中未知边的长度.
19.已知某校有一块四边形空地 如图,现计划在该空地上种草皮,经测量 , , , , .若种每平方米草皮需150元,问需投入多少元?
20.在中,,AE平分,点F为射线AE上一点(不与点E重合),且于点D.
(1)如图1,如果点F在线段AE上,且,,则_______°;
(2)如果点F在的外部,分别作出和的角平分线,交于点K,请在图2中补全图形,探究、、三者之间的数量关系,并说明理由;
(3)如图3,若点F与点A重合,PE、PC分别平分和的外角,连接PA,过点P作交BC延长线于点G,交BA的延长线于点H,若,且,请直接写出与的度数.
四、计算题
21.如图,在中,,于点,,求的长.
22.点为直线上一点,在直线同侧任作射线,,使得.
(1)如图一,过点作射线,使为的角平分线,若时,则=______°.
(2)如图二,过点作射线,当恰好为的角平分线时,另作射线,使得平分.
①若,求的度数(写出推理过程).
②若,则的度数是______(直接填空).
(3)过点作射线,当恰好为的角平分线时,另作射线,使得平分,当时,则的度数是______.(直接填空)
23.如图,C为线段上一动点,分别过点B,D作,连接.已知.
(1)求当x等于何值时,
(2)当时,求的长.
(3)利用图形求代数式的最小值.
答案解析部分
1.【答案】2
【知识点】含30°角的直角三角形
2.【答案】40
【知识点】角平分线的性质;对顶角及其性质
3.【答案】①②④
【知识点】平行线的性质;平行线的判定与性质;角平分线的性质
4.【答案】1
【知识点】勾股定理;旋转的性质
5.【答案】125
【知识点】勾股定理
6.【答案】
【知识点】等腰三角形的判定与性质;勾股定理
7.【答案】B
【知识点】勾股定理
8.【答案】C
【知识点】完全平方公式的几何背景;勾股定理
9.【答案】B
【知识点】直角三角形的性质;同位角的概念
10.【答案】C
【知识点】含30°角的直角三角形;勾股定理;旋转的性质
11.【答案】C
【知识点】勾股定理
12.【答案】C
【知识点】含30°角的直角三角形;勾股定理
13.【答案】C
【知识点】勾股定理
14.【答案】B
【知识点】三角形的面积;勾股定理
15.【答案】B
【知识点】角的运算;余角、补角及其性质;角平分线的性质
16.【答案】B
【知识点】平行线的判定与性质;角平分线的性质;对顶角及其性质
17.【答案】
【知识点】角的运算;角平分线的性质
18.【答案】(1)0;(2)
【知识点】勾股定理;求算术平方根;开立方(求立方根)
19.【答案】解:∵ , , ,
∴ ,
∵ , ,∴ ,
∴ 是直角三角形,
∴ ,
∴需投入总资金为: (元).
【知识点】勾股定理;勾股定理的逆定理
20.【答案】(1);
(2);
(3),.
【知识点】垂线的概念;三角形内角和定理;三角形的外角性质;角平分线的性质
21.【答案】
【知识点】最简二次根式;垂线的概念;勾股定理
22.【答案】(1)
(2)①②
(3)或
【知识点】角的运算;余角、补角及其性质;角平分线的性质
23.【答案】(1)
(2)
(3)
【知识点】勾股定理
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
