湘教版数学八年级下册第一次月考试题【培优】(含答案)
文档属性
| 名称 | 湘教版数学八年级下册第一次月考试题【培优】(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 695.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
湘教版数学八年级下册第一次月考试题【培优】
一、填空题
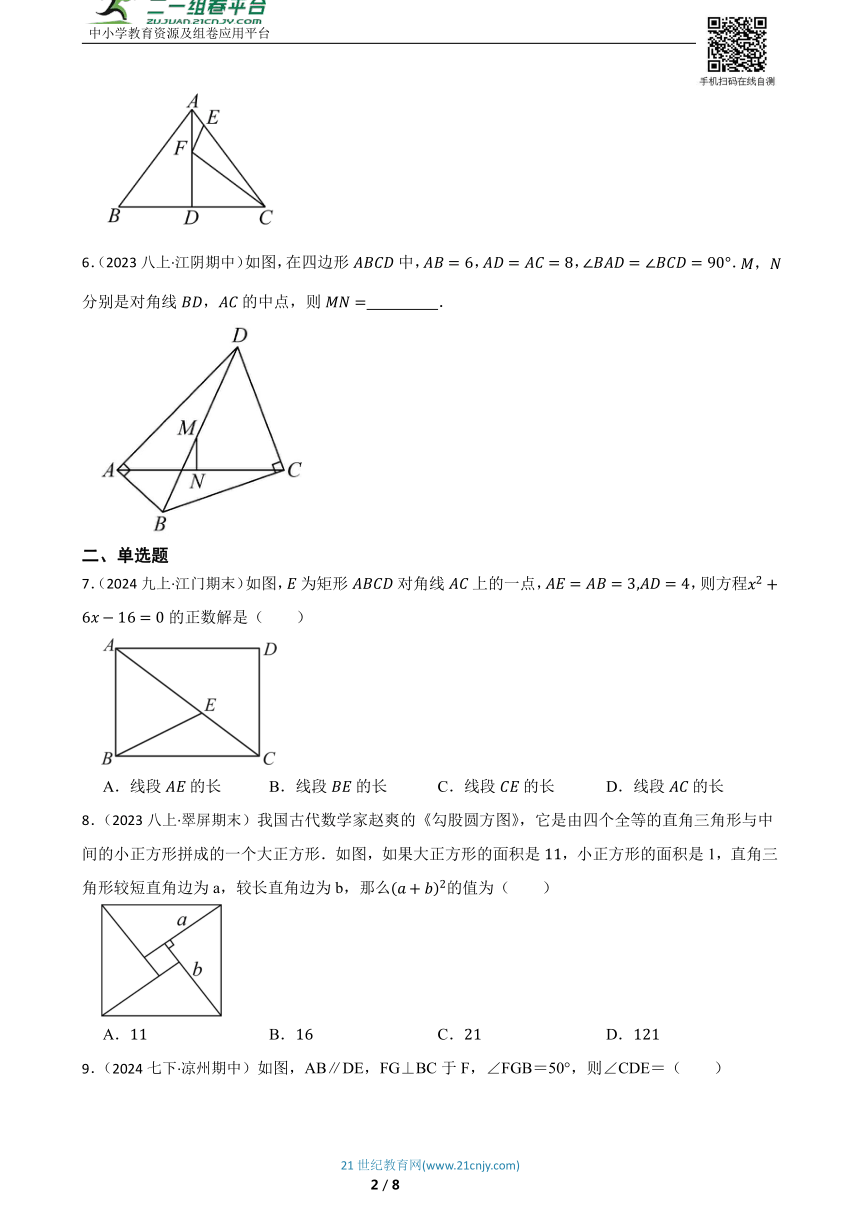
1.(2024八上·中山期中)如图,小明沿倾斜角的山坡从山脚步行到山顶,共走了,则山的高度是 .
2.(2024七下·未央期中)如图,直线与直线EF相交于点O,平分,若,则的度数为 .
3.(2023七下·江北期中)如图,已知ABCD,和的平分线交于点,,,则等于 用含、的式子表示
4.(2024九下·丹徒模拟)如图,在中,,以所在直线为轴,把旋转1周,得到一个圆锥,这个圆锥的侧面积为 .
5.(2024八上·诸暨期中)如图,中,是边上的中线,F是上的动点,E是边上的动点,则的最小值为 .
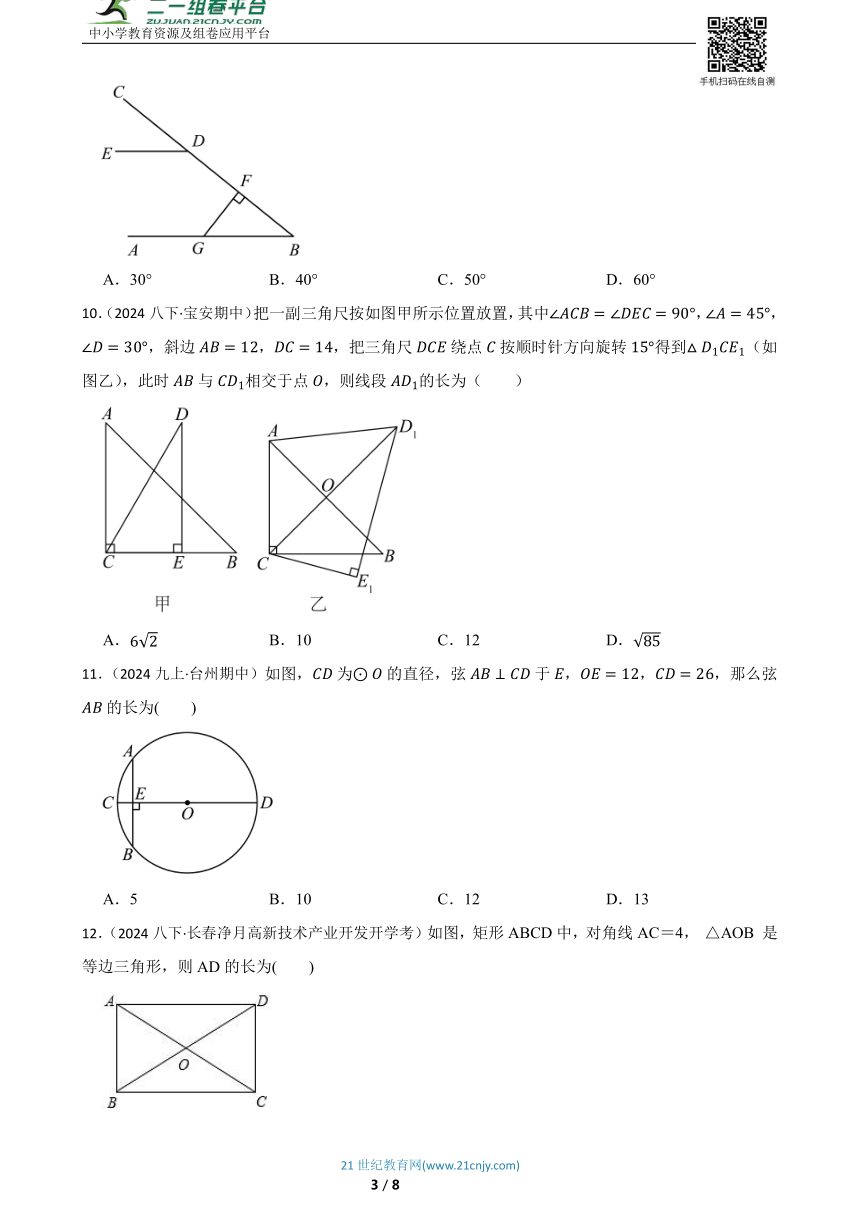
6.(2023八上·江阴期中)如图,在四边形中,,,.分别是对角线,的中点,则 .
二、单选题
7.(2024九上·江门期末)如图,为矩形对角线上的一点,,则方程的正数解是( )
A.线段的长 B.线段的长 C.线段的长 D.线段的长
8.(2023八上·翠屏期末)我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如图,如果大正方形的面积是,小正方形的面积是1,直角三角形较短直角边为a,较长直角边为b,那么的值为( )
A. B. C. D.
9.(2024七下·凉州期中)如图,AB∥DE,FG⊥BC于F,∠FGB=50°,则∠CDE=( )
A.30° B.40° C.50° D.60°
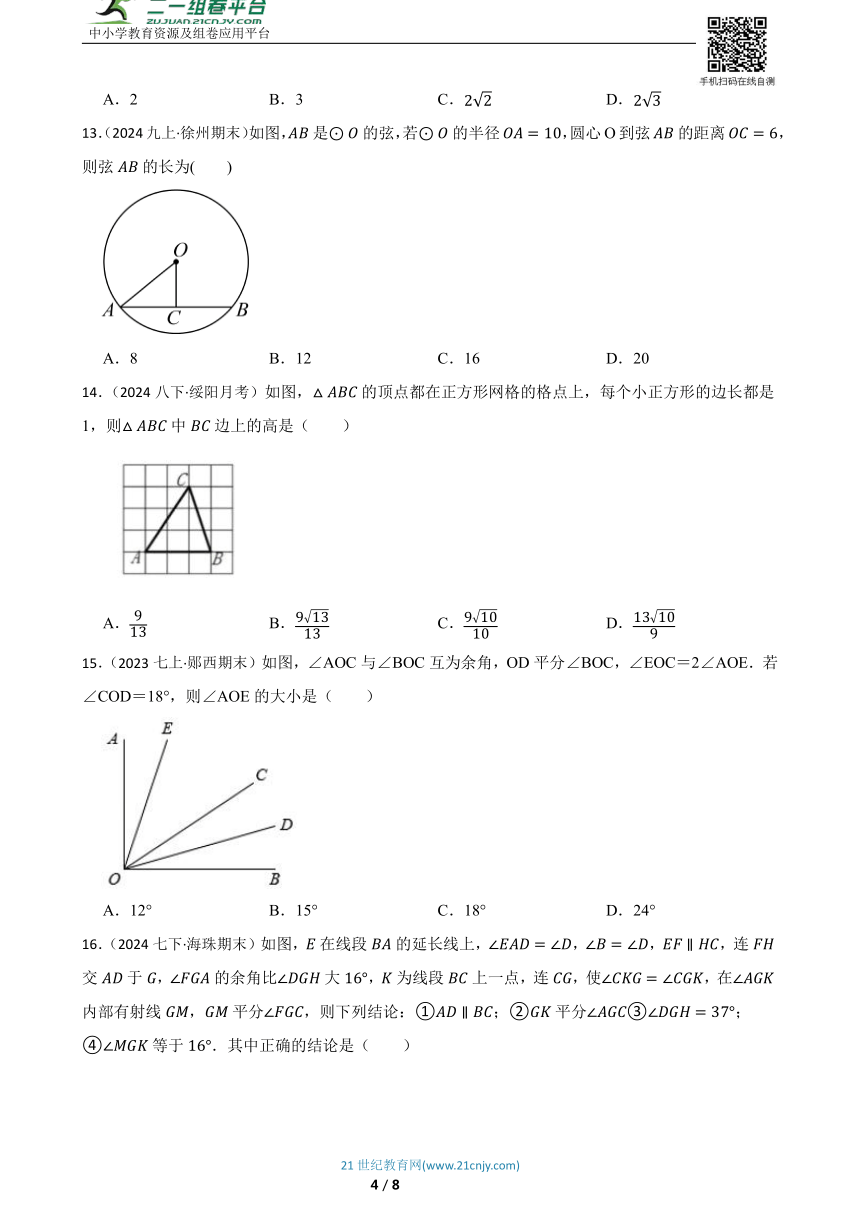
10.(2024八下·宝安期中)把一副三角尺按如图甲所示位置放置,其中,,,斜边,,把三角尺绕点按顺时针方向旋转得到(如图乙),此时与相交于点,则线段的长为( )
A. B.10 C.12 D.
11.(2024九上·台州期中)如图,为的直径,弦于,,,那么弦的长为( )
A.5 B.10 C.12 D.13
12.(2024八下·长春净月高新技术产业开发开学考)如图,矩形ABCD中,对角线AC=4, △AOB 是等边三角形,则AD的长为( )
A.2 B.3 C. D.
13.(2024九上·徐州期末)如图,是的弦,若的半径,圆心O到弦的距离,则弦的长为( )
A.8 B.12 C.16 D.20
14.(2024八下·绥阳月考)如图,的顶点都在正方形网格的格点上,每个小正方形的边长都是1,则中边上的高是( )
A. B. C. D.
15.(2023七上·郧西期末)如图,∠AOC与∠BOC互为余角,OD平分∠BOC,∠EOC=2∠AOE.若∠COD=18°,则∠AOE的大小是( )
A.12° B.15° C.18° D.24°
16.(2024七下·海珠期末)如图,在线段的延长线上,,,,连交于,的余角比大,为线段上一点,连,使,在内部有射线,平分,则下列结论:①;②平分③;④等于.其中正确的结论是( )
A.①②③ B.②③ C.①② D.①②③④
三、解答题
17.(2024七上·襄城期末)如图,是内部的一条射线,是的平分线,,,求的度数.
18.(2024八上·柴桑月考)(1)计算:.
(2)如图,求出下列直角三角形中未知边的长度.
19.(2024八下·涵江期中)如图,在珠海横琴一块三角形土地上,准备规划出阴影所示部分作为绿地,若规划图设计中∠ADC=90°,AD=8,CD=6,AB=26,BC=24,求绿地的面积.
20.(2024七下·丹徒期末)【概念】如果两个角的度数之差为,我们称这两个角互为“好友角”,其中一个角叫做另一个角的“好友角”,例如,,,则和互为“好友角”,即是的“好友角”,也是的“好友角”.
【理解】(1)若,则的“好友角”的度数为 ;
(2)已知和互为“好友角”,,且和互补,的度数为 ;
(3)如图,将纸片沿折叠,使点落在四边形内部处,已知,,若和互为“好友角”,则的度数为 ;
【拓展】如图,在中,,是角平分线,过点作的垂线,垂足为,相交于点.若与互为“好友角”,求的度数.
四、计算题
21.(2024八下·仓山期中)如图,在中,,于点,,求的长.
22.(2023七上·路北期末)如图,点O为直线上一点,,平分.
(1)求的度数;
(2)作射线,若与互余,求的度数.
23.(2024八下·凉州期末)已知:如图,四边形中,,,,,,求四边形的面积.
答案解析部分
1.【答案】
【知识点】含30°角的直角三角形
2.【答案】120°
【知识点】垂线的概念;角平分线的性质;对顶角及其性质
3.【答案】(90+)
【知识点】平行线的性质;平行线的判定与性质;角平分线的性质
4.【答案】
【知识点】勾股定理;圆锥的计算;旋转的性质
5.【答案】4.8
【知识点】两点之间线段最短;等腰三角形的性质;勾股定理
6.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;直角三角形斜边上的中线
7.【答案】C
【知识点】因式分解法解一元二次方程;勾股定理;矩形的性质
8.【答案】C
【知识点】完全平方公式的几何背景;勾股定理
9.【答案】B
【知识点】直角三角形的性质;同位角的概念
10.【答案】B
【知识点】含30°角的直角三角形;勾股定理;旋转的性质
11.【答案】B
【知识点】勾股定理;垂径定理
12.【答案】D
【知识点】含30°角的直角三角形;勾股定理;矩形的性质
13.【答案】C
【知识点】勾股定理;垂径定理
14.【答案】C
【知识点】三角形的面积;勾股定理
15.【答案】C
【知识点】角的运算;余角、补角及其性质;角平分线的性质
16.【答案】A
【知识点】平行线的判定与性质;角平分线的性质;对顶角及其性质
17.【答案】
【知识点】角的运算;角平分线的性质
18.【答案】(1)0;(2)
【知识点】勾股定理;求算术平方根;开立方(求立方根)
19.【答案】绿地的面积为96
【知识点】勾股定理;勾股定理的逆定理
20.【答案】【理解】()或;();()或;
【拓展】或.
【知识点】垂线的概念;三角形内角和定理;三角形的外角性质;角平分线的性质
21.【答案】
【知识点】最简二次根式;垂线的概念;勾股定理
22.【答案】(1)
(2)或
【知识点】角的运算;余角、补角及其性质;角平分线的性质
23.【答案】
【知识点】勾股定理;勾股定理的逆定理
21世纪教育网(www.21cnjy.com)
2 / 8
湘教版数学八年级下册第一次月考试题【培优】
一、填空题
1.(2024八上·中山期中)如图,小明沿倾斜角的山坡从山脚步行到山顶,共走了,则山的高度是 .
2.(2024七下·未央期中)如图,直线与直线EF相交于点O,平分,若,则的度数为 .
3.(2023七下·江北期中)如图,已知ABCD,和的平分线交于点,,,则等于 用含、的式子表示
4.(2024九下·丹徒模拟)如图,在中,,以所在直线为轴,把旋转1周,得到一个圆锥,这个圆锥的侧面积为 .
5.(2024八上·诸暨期中)如图,中,是边上的中线,F是上的动点,E是边上的动点,则的最小值为 .
6.(2023八上·江阴期中)如图,在四边形中,,,.分别是对角线,的中点,则 .
二、单选题
7.(2024九上·江门期末)如图,为矩形对角线上的一点,,则方程的正数解是( )
A.线段的长 B.线段的长 C.线段的长 D.线段的长
8.(2023八上·翠屏期末)我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如图,如果大正方形的面积是,小正方形的面积是1,直角三角形较短直角边为a,较长直角边为b,那么的值为( )
A. B. C. D.
9.(2024七下·凉州期中)如图,AB∥DE,FG⊥BC于F,∠FGB=50°,则∠CDE=( )
A.30° B.40° C.50° D.60°
10.(2024八下·宝安期中)把一副三角尺按如图甲所示位置放置,其中,,,斜边,,把三角尺绕点按顺时针方向旋转得到(如图乙),此时与相交于点,则线段的长为( )
A. B.10 C.12 D.
11.(2024九上·台州期中)如图,为的直径,弦于,,,那么弦的长为( )
A.5 B.10 C.12 D.13
12.(2024八下·长春净月高新技术产业开发开学考)如图,矩形ABCD中,对角线AC=4, △AOB 是等边三角形,则AD的长为( )
A.2 B.3 C. D.
13.(2024九上·徐州期末)如图,是的弦,若的半径,圆心O到弦的距离,则弦的长为( )
A.8 B.12 C.16 D.20
14.(2024八下·绥阳月考)如图,的顶点都在正方形网格的格点上,每个小正方形的边长都是1,则中边上的高是( )
A. B. C. D.
15.(2023七上·郧西期末)如图,∠AOC与∠BOC互为余角,OD平分∠BOC,∠EOC=2∠AOE.若∠COD=18°,则∠AOE的大小是( )
A.12° B.15° C.18° D.24°
16.(2024七下·海珠期末)如图,在线段的延长线上,,,,连交于,的余角比大,为线段上一点,连,使,在内部有射线,平分,则下列结论:①;②平分③;④等于.其中正确的结论是( )
A.①②③ B.②③ C.①② D.①②③④
三、解答题
17.(2024七上·襄城期末)如图,是内部的一条射线,是的平分线,,,求的度数.
18.(2024八上·柴桑月考)(1)计算:.
(2)如图,求出下列直角三角形中未知边的长度.
19.(2024八下·涵江期中)如图,在珠海横琴一块三角形土地上,准备规划出阴影所示部分作为绿地,若规划图设计中∠ADC=90°,AD=8,CD=6,AB=26,BC=24,求绿地的面积.
20.(2024七下·丹徒期末)【概念】如果两个角的度数之差为,我们称这两个角互为“好友角”,其中一个角叫做另一个角的“好友角”,例如,,,则和互为“好友角”,即是的“好友角”,也是的“好友角”.
【理解】(1)若,则的“好友角”的度数为 ;
(2)已知和互为“好友角”,,且和互补,的度数为 ;
(3)如图,将纸片沿折叠,使点落在四边形内部处,已知,,若和互为“好友角”,则的度数为 ;
【拓展】如图,在中,,是角平分线,过点作的垂线,垂足为,相交于点.若与互为“好友角”,求的度数.
四、计算题
21.(2024八下·仓山期中)如图,在中,,于点,,求的长.
22.(2023七上·路北期末)如图,点O为直线上一点,,平分.
(1)求的度数;
(2)作射线,若与互余,求的度数.
23.(2024八下·凉州期末)已知:如图,四边形中,,,,,,求四边形的面积.
答案解析部分
1.【答案】
【知识点】含30°角的直角三角形
2.【答案】120°
【知识点】垂线的概念;角平分线的性质;对顶角及其性质
3.【答案】(90+)
【知识点】平行线的性质;平行线的判定与性质;角平分线的性质
4.【答案】
【知识点】勾股定理;圆锥的计算;旋转的性质
5.【答案】4.8
【知识点】两点之间线段最短;等腰三角形的性质;勾股定理
6.【答案】
【知识点】等腰三角形的判定与性质;勾股定理;直角三角形斜边上的中线
7.【答案】C
【知识点】因式分解法解一元二次方程;勾股定理;矩形的性质
8.【答案】C
【知识点】完全平方公式的几何背景;勾股定理
9.【答案】B
【知识点】直角三角形的性质;同位角的概念
10.【答案】B
【知识点】含30°角的直角三角形;勾股定理;旋转的性质
11.【答案】B
【知识点】勾股定理;垂径定理
12.【答案】D
【知识点】含30°角的直角三角形;勾股定理;矩形的性质
13.【答案】C
【知识点】勾股定理;垂径定理
14.【答案】C
【知识点】三角形的面积;勾股定理
15.【答案】C
【知识点】角的运算;余角、补角及其性质;角平分线的性质
16.【答案】A
【知识点】平行线的判定与性质;角平分线的性质;对顶角及其性质
17.【答案】
【知识点】角的运算;角平分线的性质
18.【答案】(1)0;(2)
【知识点】勾股定理;求算术平方根;开立方(求立方根)
19.【答案】绿地的面积为96
【知识点】勾股定理;勾股定理的逆定理
20.【答案】【理解】()或;();()或;
【拓展】或.
【知识点】垂线的概念;三角形内角和定理;三角形的外角性质;角平分线的性质
21.【答案】
【知识点】最简二次根式;垂线的概念;勾股定理
22.【答案】(1)
(2)或
【知识点】角的运算;余角、补角及其性质;角平分线的性质
23.【答案】
【知识点】勾股定理;勾股定理的逆定理
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
