湘教版数学八年级下册期末综合复习题(含答案)
文档属性
| 名称 | 湘教版数学八年级下册期末综合复习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 526.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
湘教版数学八年级下册期末综合复习题
一、单选题
1.一次函数的函数值y随x的增大而减小,则k的取值范围( )
A. B. C. D.
2.如图有两棵树,一棵高14,一堁高2,两树之间相距5,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了( )米?
A.11 B.12 C.13 D.14
3.函数的图象是( )
A.一条射线 B.一条直线 C.一条线段 D.一条曲线
4.一个等腰三角形的两边长分别为,,则这个三角形的周长为( )
A. B.
C. D.以上答案都不对
5.若一个三角形的三边长的平方分别为:32,42,x2则此三角形是直角三角形的x2的值是( )
A.4 B.52 C.7 D.52或7
6.汽车离开甲站10千米后,以60千米/时的速度匀速前进了小时,则汽车离开甲站所走的路程(千米)与时间(小时)之间的关系式是( )
A. B. C. D.
7.已知线段、、首尾相连后能构成直角三角形,若,,则的长为( )
A.或 B.或 C. D.
8.点,点都在直线上,则和的大小关系是( )
A. B. C. D.不能确定
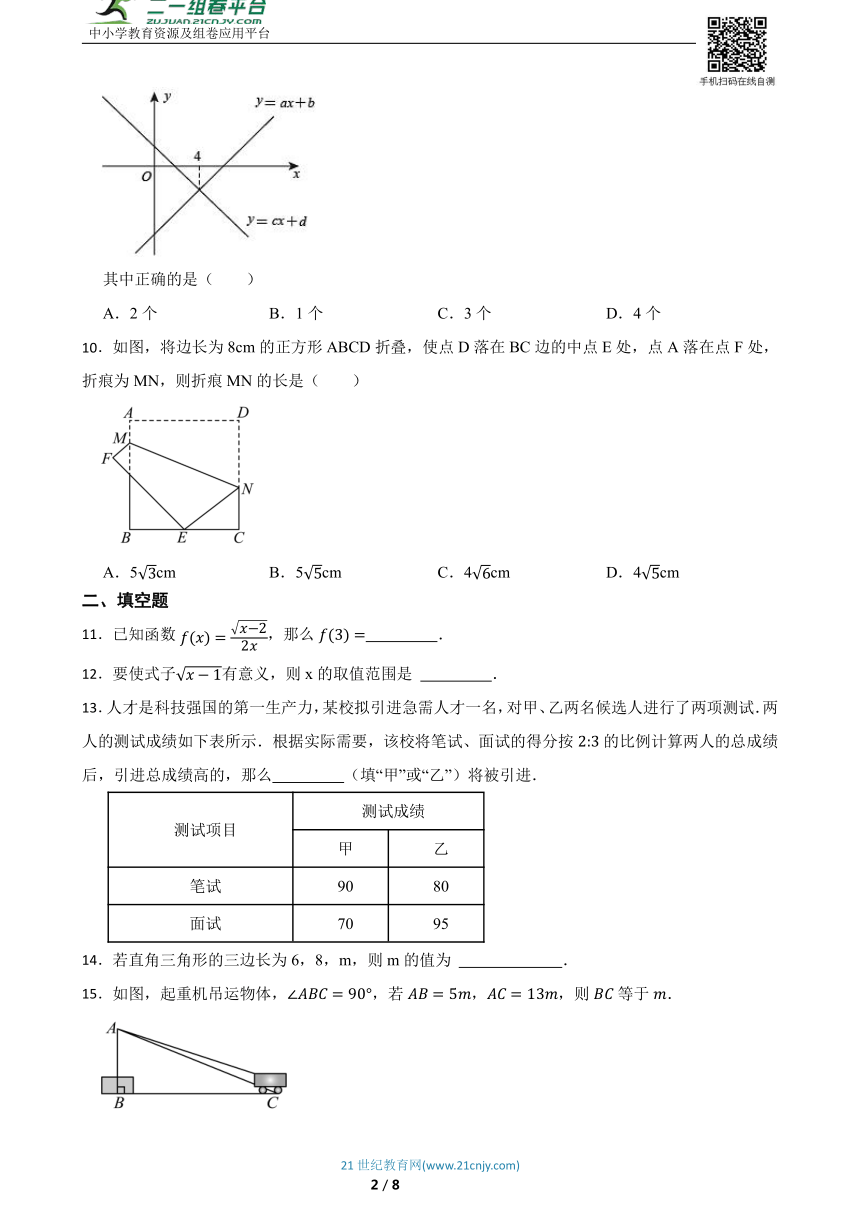
9.如图所示,一次函数与的图象如图所示,下列说法:
①对于函数来说,y随x的增大而增大;②函数不经过第四象限;
③不等式的解集是;④.
其中正确的是( )
A.2个 B.1个 C.3个 D.4个
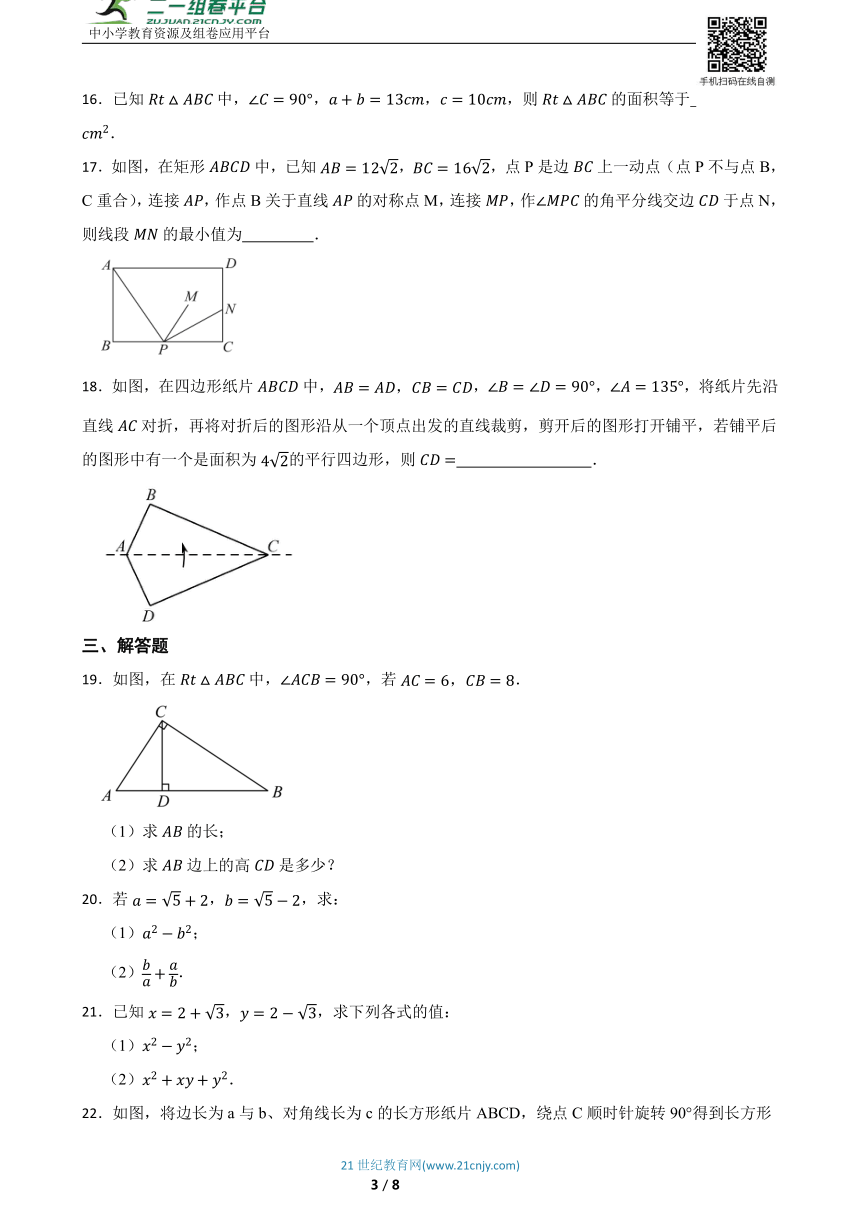
10.如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则折痕MN的长是( )
A.5cm B.5cm C.4cm D.4cm
二、填空题
11.已知函数,那么 .
12.要使式子有意义,则x的取值范围是 .
13.人才是科技强国的第一生产力,某校拟引进急需人才一名,对甲、乙两名候选人进行了两项测试.两人的测试成绩如下表所示.根据实际需要,该校将笔试、面试的得分按的比例计算两人的总成绩后,引进总成绩高的,那么 (填“甲”或“乙”)将被引进.
测试项目 测试成绩
甲 乙
笔试 90 80
面试 70 95
14.若直角三角形的三边长为6,8,m,则m的值为 .
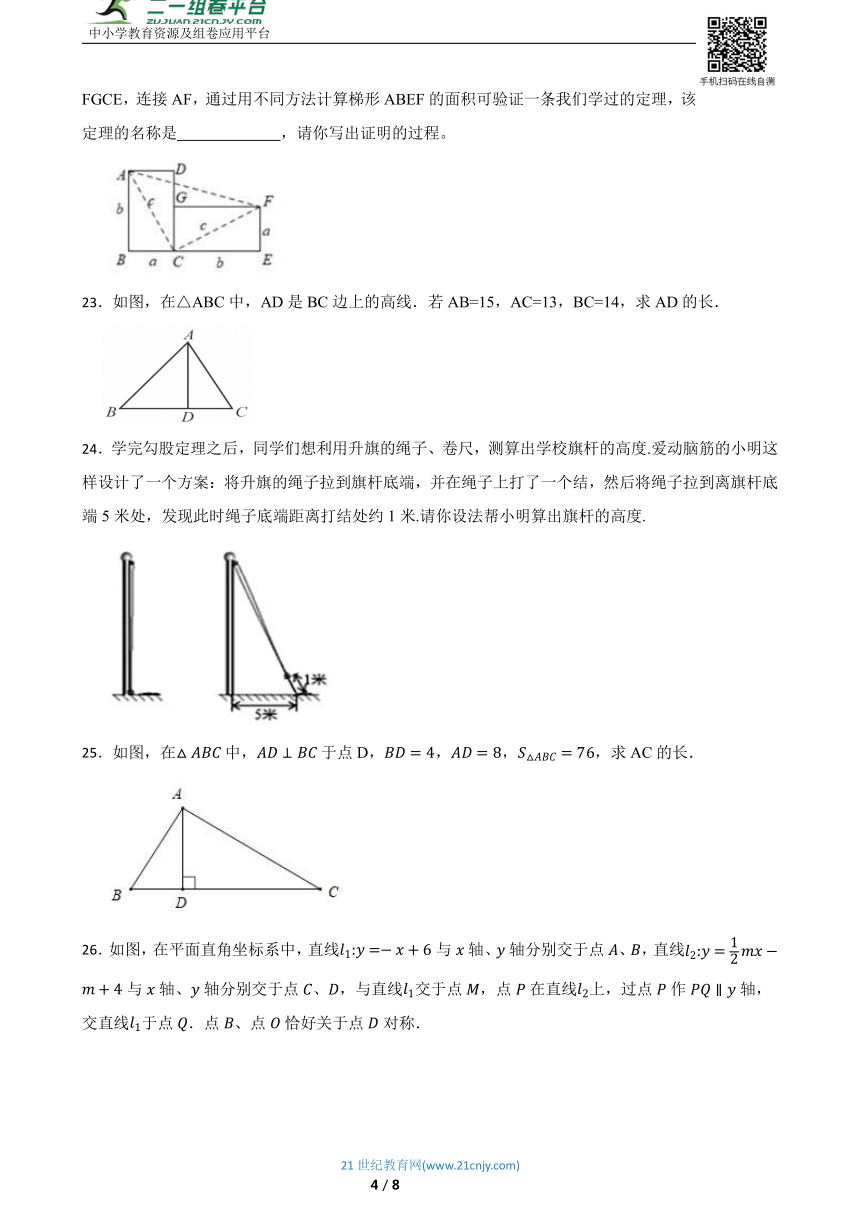
15.如图,起重机吊运物体,,若,,则等于.
16.已知中,,,,则的面积等于 .
17.如图,在矩形中,已知,,点P是边上一动点(点P不与点B,C重合),连接,作点B关于直线的对称点M,连接,作的角平分线交边于点N,则线段的最小值为 .
18.如图,在四边形纸片中,,,,将纸片先沿直线对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为的平行四边形,则 .
三、解答题
19.如图,在中,,若.
(1)求的长;
(2)求边上的高是多少?
20.若,,求:
(1);
(2).
21.已知,,求下列各式的值:
(1);
(2).
22.如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF,通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是 ,请你写出证明的过程。
23.如图,在△ABC中,AD是BC边上的高线.若AB=15,AC=13,BC=14,求AD的长.
24.学完勾股定理之后,同学们想利用升旗的绳子、卷尺,测算出学校旗杆的高度.爱动脑筋的小明这样设计了一个方案:将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现此时绳子底端距离打结处约1米.请你设法帮小明算出旗杆的高度.
25.如图,在中,于点D,,,,求AC的长.
26.如图,在平面直角坐标系中,直线与轴、轴分别交于点、,直线与轴、轴分别交于点、,与直线交于点,点在直线上,过点作轴,交直线于点.点、点恰好关于点对称.
(1)求直线的解析式;
(2)求的面积;
(3)如果线段的长为,求点的坐标;
(4)我们规定:横坐标和纵坐标都是整数的点叫整点.如果,直接写出所有符合条件的整点的坐标.
27.求使 有意义的x的取值范围.
28.如图,正方形的边、在坐标轴上,点的坐标为.点从点A 出发,以每秒个单位长度的速度沿轴向点运动;点从点同时出发,以相同的速度沿轴的正方向运动,规定点到达点时,点也停止运动.连接,过点作的垂线,与过点平行于轴的直线相交于点.与轴交于点,连接.设点运动的时间为.
(1)的度数为_________,点的坐标为___________(用表示);
(2)在的运动过程中,直线的解析式发生变化吗?如果不变,请直接写出直线的解析式;
(3)探索的周长是否随时间的变化而变化,若变化,说明理由;若不变,试求这个定值.
答案解析部分
1.【答案】D
【知识点】一次函数的性质
2.【答案】C
【知识点】勾股定理的应用
3.【答案】A
【知识点】一次函数的图象
4.【答案】B
【知识点】二次根式的性质与化简;三角形三边关系;等腰三角形的概念
5.【答案】D
【知识点】勾股定理
6.【答案】A
【知识点】列一次函数关系式
7.【答案】A
【知识点】勾股定理
8.【答案】A
【知识点】一次函数的概念
9.【答案】C
【知识点】一次函数与不等式(组)的关系
10.【答案】D
【知识点】勾股定理;正方形的性质
11.【答案】
【知识点】分式有无意义的条件;二次根式有意义的条件;函数自变量的取值范围
12.【答案】
【知识点】二次根式有意义的条件;解一元一次不等式
13.【答案】乙
【知识点】加权平均数及其计算
14.【答案】或
【知识点】勾股定理
15.【答案】
【知识点】勾股定理
16.【答案】
【知识点】完全平方公式及运用;勾股定理
17.【答案】
【知识点】勾股定理;矩形的性质;轴对称的性质
18.【答案】或
【知识点】等腰三角形的判定;勾股定理;平行四边形的性质;菱形的判定与性质
19.【答案】(1)
(2)
【知识点】勾股定理
20.【答案】(1);
(2)18.
【知识点】分式的化简求值;二次根式的化简求值
21.【答案】(1)
(2)15
【知识点】完全平方公式及运用;二次根式的乘除法;二次根式的化简求值
22.【答案】勾股定理
【知识点】勾股定理的证明
23.【答案】解:设 , 则 . 由勾股定理, 得 ,
即 , 解得 ,
所以 , 得
【知识点】勾股定理
24.【答案】解:设旗杆长为x米,则绳长为(x+1)米,则由勾股定理可得:
,
解得x=12,
答:旗杆的高度为12米.
【知识点】勾股定理的应用
25.【答案】解:∵,,
∴,即,
∵,,
∴,
解得: ,
在 中,由勾股定理得:
.
【知识点】三角形的面积;勾股定理
26.【答案】(1)
(2)
(3)点坐标为或
(4)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数图象与坐标轴交点问题;化简含绝对值有理数
27.【答案】【解答】由原式得x-3>0,4-x>0,综上得3【知识点】二次根式的性质与化简
28.【答案】(1),
(2)
(3)不变,值为8
【知识点】待定系数法求一次函数解析式;等腰三角形的判定与性质;正方形的性质
21世纪教育网(www.21cnjy.com)
2 / 8
湘教版数学八年级下册期末综合复习题
一、单选题
1.一次函数的函数值y随x的增大而减小,则k的取值范围( )
A. B. C. D.
2.如图有两棵树,一棵高14,一堁高2,两树之间相距5,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了( )米?
A.11 B.12 C.13 D.14
3.函数的图象是( )
A.一条射线 B.一条直线 C.一条线段 D.一条曲线
4.一个等腰三角形的两边长分别为,,则这个三角形的周长为( )
A. B.
C. D.以上答案都不对
5.若一个三角形的三边长的平方分别为:32,42,x2则此三角形是直角三角形的x2的值是( )
A.4 B.52 C.7 D.52或7
6.汽车离开甲站10千米后,以60千米/时的速度匀速前进了小时,则汽车离开甲站所走的路程(千米)与时间(小时)之间的关系式是( )
A. B. C. D.
7.已知线段、、首尾相连后能构成直角三角形,若,,则的长为( )
A.或 B.或 C. D.
8.点,点都在直线上,则和的大小关系是( )
A. B. C. D.不能确定
9.如图所示,一次函数与的图象如图所示,下列说法:
①对于函数来说,y随x的增大而增大;②函数不经过第四象限;
③不等式的解集是;④.
其中正确的是( )
A.2个 B.1个 C.3个 D.4个
10.如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则折痕MN的长是( )
A.5cm B.5cm C.4cm D.4cm
二、填空题
11.已知函数,那么 .
12.要使式子有意义,则x的取值范围是 .
13.人才是科技强国的第一生产力,某校拟引进急需人才一名,对甲、乙两名候选人进行了两项测试.两人的测试成绩如下表所示.根据实际需要,该校将笔试、面试的得分按的比例计算两人的总成绩后,引进总成绩高的,那么 (填“甲”或“乙”)将被引进.
测试项目 测试成绩
甲 乙
笔试 90 80
面试 70 95
14.若直角三角形的三边长为6,8,m,则m的值为 .
15.如图,起重机吊运物体,,若,,则等于.
16.已知中,,,,则的面积等于 .
17.如图,在矩形中,已知,,点P是边上一动点(点P不与点B,C重合),连接,作点B关于直线的对称点M,连接,作的角平分线交边于点N,则线段的最小值为 .
18.如图,在四边形纸片中,,,,将纸片先沿直线对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为的平行四边形,则 .
三、解答题
19.如图,在中,,若.
(1)求的长;
(2)求边上的高是多少?
20.若,,求:
(1);
(2).
21.已知,,求下列各式的值:
(1);
(2).
22.如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF,通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是 ,请你写出证明的过程。
23.如图,在△ABC中,AD是BC边上的高线.若AB=15,AC=13,BC=14,求AD的长.
24.学完勾股定理之后,同学们想利用升旗的绳子、卷尺,测算出学校旗杆的高度.爱动脑筋的小明这样设计了一个方案:将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现此时绳子底端距离打结处约1米.请你设法帮小明算出旗杆的高度.
25.如图,在中,于点D,,,,求AC的长.
26.如图,在平面直角坐标系中,直线与轴、轴分别交于点、,直线与轴、轴分别交于点、,与直线交于点,点在直线上,过点作轴,交直线于点.点、点恰好关于点对称.
(1)求直线的解析式;
(2)求的面积;
(3)如果线段的长为,求点的坐标;
(4)我们规定:横坐标和纵坐标都是整数的点叫整点.如果,直接写出所有符合条件的整点的坐标.
27.求使 有意义的x的取值范围.
28.如图,正方形的边、在坐标轴上,点的坐标为.点从点A 出发,以每秒个单位长度的速度沿轴向点运动;点从点同时出发,以相同的速度沿轴的正方向运动,规定点到达点时,点也停止运动.连接,过点作的垂线,与过点平行于轴的直线相交于点.与轴交于点,连接.设点运动的时间为.
(1)的度数为_________,点的坐标为___________(用表示);
(2)在的运动过程中,直线的解析式发生变化吗?如果不变,请直接写出直线的解析式;
(3)探索的周长是否随时间的变化而变化,若变化,说明理由;若不变,试求这个定值.
答案解析部分
1.【答案】D
【知识点】一次函数的性质
2.【答案】C
【知识点】勾股定理的应用
3.【答案】A
【知识点】一次函数的图象
4.【答案】B
【知识点】二次根式的性质与化简;三角形三边关系;等腰三角形的概念
5.【答案】D
【知识点】勾股定理
6.【答案】A
【知识点】列一次函数关系式
7.【答案】A
【知识点】勾股定理
8.【答案】A
【知识点】一次函数的概念
9.【答案】C
【知识点】一次函数与不等式(组)的关系
10.【答案】D
【知识点】勾股定理;正方形的性质
11.【答案】
【知识点】分式有无意义的条件;二次根式有意义的条件;函数自变量的取值范围
12.【答案】
【知识点】二次根式有意义的条件;解一元一次不等式
13.【答案】乙
【知识点】加权平均数及其计算
14.【答案】或
【知识点】勾股定理
15.【答案】
【知识点】勾股定理
16.【答案】
【知识点】完全平方公式及运用;勾股定理
17.【答案】
【知识点】勾股定理;矩形的性质;轴对称的性质
18.【答案】或
【知识点】等腰三角形的判定;勾股定理;平行四边形的性质;菱形的判定与性质
19.【答案】(1)
(2)
【知识点】勾股定理
20.【答案】(1);
(2)18.
【知识点】分式的化简求值;二次根式的化简求值
21.【答案】(1)
(2)15
【知识点】完全平方公式及运用;二次根式的乘除法;二次根式的化简求值
22.【答案】勾股定理
【知识点】勾股定理的证明
23.【答案】解:设 , 则 . 由勾股定理, 得 ,
即 , 解得 ,
所以 , 得
【知识点】勾股定理
24.【答案】解:设旗杆长为x米,则绳长为(x+1)米,则由勾股定理可得:
,
解得x=12,
答:旗杆的高度为12米.
【知识点】勾股定理的应用
25.【答案】解:∵,,
∴,即,
∵,,
∴,
解得: ,
在 中,由勾股定理得:
.
【知识点】三角形的面积;勾股定理
26.【答案】(1)
(2)
(3)点坐标为或
(4)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;一次函数图象与坐标轴交点问题;化简含绝对值有理数
27.【答案】【解答】由原式得x-3>0,4-x>0,综上得3
28.【答案】(1),
(2)
(3)不变,值为8
【知识点】待定系数法求一次函数解析式;等腰三角形的判定与性质;正方形的性质
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
