湘教版数学八年级下册期末试题【培优】(含答案)
文档属性
| 名称 | 湘教版数学八年级下册期末试题【培优】(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 468.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版数学八年级下册期末试题【培优】
一、填空题
1.(2022八下·碧江月考)在中,,则 .
2.(2022八上·衡东期中)如图,正方形的边长为4,点E在AB边上.四边形也为正方形,设的面积为S,则 .
3.(2023八下·泉港期末)在中,.则的度数为 .
4.(2024八下·武昌期末)腰为,高为的等腰三角形的底边长为 .
5.(2024八上·景泰期中)在一个不透明的袋子中,装有11个白球和若干个红球,它们除颜色外完全相同,若小李通过多次摸球试验后发现其中摸到红色玻璃球的频率稳定在,则袋子中有 个红球.
6.(2023八下·庐阳期末)如图,中,,,点是的中点.
(1)当时,则 ;
(2)点在上,且,过点分别作于点,于点,则 .
二、单选题
7.(2023八上·嘉鱼期末)点关于y轴对称的点的坐标是( )
A. B. C. D.
8.(2024八下·顺德期末)正六边形的内角和是( )
A. B. C. D.
9.(2022八下·武汉月考)下命题中,是真命题的是( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形
D.两条对角线互相垂直的平行四边形是正方形
10.(2024九上·北京市开学考)变量x与y之间的关系是,当时,自变量x的值是( )
A.13 B.5 C.2 D.3
11.(2022八下·大足期中)已知三角形的三边长分别为5,12,13,这是一个( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
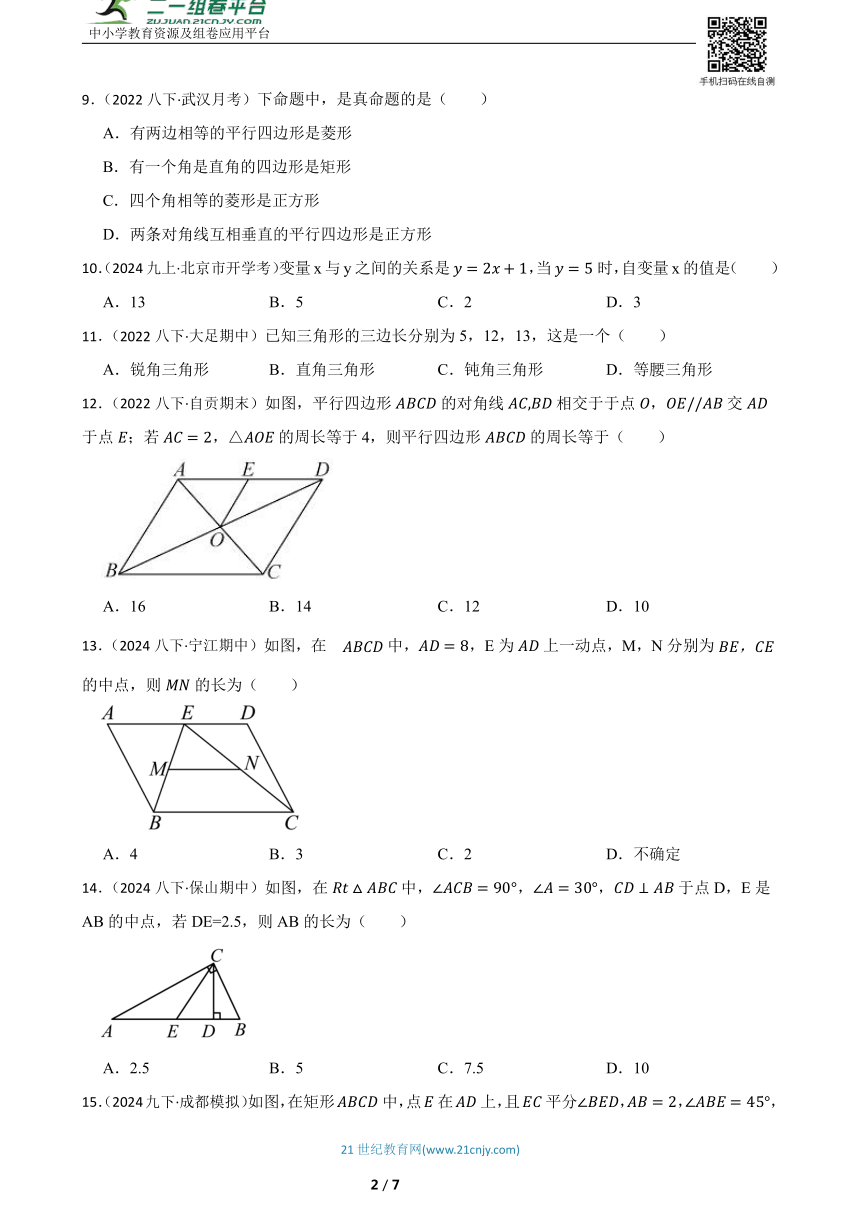
12.(2022八下·自贡期末)如图,平行四边形的对角线相交于于点,交于点;若,△的周长等于4,则平行四边形的周长等于( )
A.16 B.14 C.12 D.10
13.(2024八下·宁江期中)如图,在中,,E为上一动点,M,N分别为的中点,则的长为( )
A.4 B.3 C.2 D.不确定
14.(2024八下·保山期中)如图,在中,,,于点D,E是AB的中点,若DE=2.5,则AB的长为( )
A.2.5 B.5 C.7.5 D.10
15.(2024九下·成都模拟)如图,在矩形中,点在上,且平分,,,则的长为( )
A. B. C. D.
16.(2023九上·包河开学考)如图,在菱形中,,是边上一点,且,有下列结论:
是等边三角形;
;
周长的最小值为;
面积的最大值为.
其中正确结论有( )
A.个 B.个 C.个 D.个
三、解答题
17.(2023七上·天长期中)生活处处有数学,就看你是否有数学的眼光.同学们都见过机械手表吧,让我们一起去探索其中隐含的数学知识
一块手表如图①所示,把它抽象成数学模型:如图②,表带的两端用点A和点表示,表盘与线段交于点、,为表盘圆心.
(1)若为,,是中点,则手表全长______.
(2)表盘上的点对应数字“12”,点对应数字“6”,为时针,为分针,时表盘指针状态如图③所示,分针与重合.
①______度;
②作射线,使,求此时的度数.
18.(2024七下·霍林郭勒期中)在平面直角坐标系中,已知点,若点M到x轴的距离等于5,求m的值.
19.(2023九下·龙江模拟)甲、乙两车分别从相距的M、N两地出发,匀速行驶,先相向而行,乙车在甲车出发后出发,到达M地后停止行驶,甲车到达N地后,立即按原路原速返回M地(甲车调头的时间忽略不计),甲、乙两车距N地的路程y(单位:)与甲车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)甲车的行驶速度是 ,乙车的行驶速度是 , ;
(2)求线段的解析式并写出自变量的取值范围;
(3)乙车出发多少小时后两车相距为?请直接写出答案.
20.(2024八下·北京市期末)定义:对于给定的一次函数. 把形如 的函数称为一次函数的衍生函数.
(1)已知函数, 若点 在这个一次函数的衍生函数图象上,则 ,
(2)已知矩形的顶点坐标分别为,当函数的衍生函数的图象与矩形有1个交点时 .当函数)的衍生函数的图象与矩形有两个交点时,直接写出k的取值范围 .
(3)已知点,以为一条对角线作正方形,当正方形与一次函数的衍生函数图象有两个交点时,求t的取值范围.
四、计算题
21.(2019·怀化模拟)设一次函数y=kx+b(k≠0)的图象经过A(1,3),B(0,-2)两点,试求k,b的值.
22.(2024七下·新华期末)如图,在中,平分,P为线段上的一点,过点P作交的延长线于点E.若,,求的度数.
23.(2024八下·东西湖期末)在菱形中,,点E、F分别为上一点.
(1)如图1,当,时,直接写出三条线段和之间满足的等量关系式为________;
(2)当时,
①如图2,若,若,,求的长;
②如图3,E为中点,交于点G,交于点H,和交于点O,若,,,则________.
答案解析部分
1.【答案】或
【知识点】直角三角形的性质
2.【答案】8
【知识点】平行线之间的距离;正方形的性质
3.【答案】
【知识点】平行四边形的性质
4.【答案】
【知识点】等腰三角形的性质;勾股定理
5.【答案】9
【知识点】解分式方程;频数与频率
6.【答案】(1)
(2)
【知识点】勾股定理的应用
7.【答案】A
【知识点】坐标与图形变化﹣对称
8.【答案】C
【知识点】多边形内角与外角
9.【答案】C
【知识点】菱形的判定;矩形的判定;正方形的判定
10.【答案】C
【知识点】函数自变量的取值范围
11.【答案】B
【知识点】勾股定理的逆定理
12.【答案】C
【知识点】平行四边形的性质;三角形的中位线定理
13.【答案】A
【知识点】平行四边形的性质;三角形的中位线定理
14.【答案】D
【知识点】等边三角形的判定与性质;含30°角的直角三角形;直角三角形斜边上的中线
15.【答案】A
【知识点】勾股定理;矩形的性质
16.【答案】D
【知识点】等边三角形的判定与性质;菱形的性质
17.【答案】(1)
(2)①;②在内部时,,在外部时
【知识点】角的运算;角平分线的性质;线段的和、差、倍、分的简单计算;钟面角
18.【答案】6或1
【知识点】点的坐标
19.【答案】(1),,240;
(2)
(3)或或
【知识点】待定系数法求一次函数解析式;一元一次方程的实际应用-行程问题;通过函数图象获取信息
20.【答案】(1)2 , 3
(2)1,
(3)或 或
【知识点】一次函数的概念;矩形的性质;正方形的性质
21.【答案】解:把A(1,3)、B(0,﹣2)代入y=kx+b得 ,
解得 ,
故k,b的值分别为5,﹣2.
【知识点】待定系数法求一次函数解析式
22.【答案】
【知识点】三角形的角平分线、中线和高;三角形内角和定理;三角形的外角性质;直角三角形的性质
23.【答案】(1)
(2);
【知识点】等边三角形的判定与性质;勾股定理;正方形的性质
21世纪教育网(www.21cnjy.com)
2 / 7
湘教版数学八年级下册期末试题【培优】
一、填空题
1.(2022八下·碧江月考)在中,,则 .
2.(2022八上·衡东期中)如图,正方形的边长为4,点E在AB边上.四边形也为正方形,设的面积为S,则 .
3.(2023八下·泉港期末)在中,.则的度数为 .
4.(2024八下·武昌期末)腰为,高为的等腰三角形的底边长为 .
5.(2024八上·景泰期中)在一个不透明的袋子中,装有11个白球和若干个红球,它们除颜色外完全相同,若小李通过多次摸球试验后发现其中摸到红色玻璃球的频率稳定在,则袋子中有 个红球.
6.(2023八下·庐阳期末)如图,中,,,点是的中点.
(1)当时,则 ;
(2)点在上,且,过点分别作于点,于点,则 .
二、单选题
7.(2023八上·嘉鱼期末)点关于y轴对称的点的坐标是( )
A. B. C. D.
8.(2024八下·顺德期末)正六边形的内角和是( )
A. B. C. D.
9.(2022八下·武汉月考)下命题中,是真命题的是( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形
D.两条对角线互相垂直的平行四边形是正方形
10.(2024九上·北京市开学考)变量x与y之间的关系是,当时,自变量x的值是( )
A.13 B.5 C.2 D.3
11.(2022八下·大足期中)已知三角形的三边长分别为5,12,13,这是一个( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
12.(2022八下·自贡期末)如图,平行四边形的对角线相交于于点,交于点;若,△的周长等于4,则平行四边形的周长等于( )
A.16 B.14 C.12 D.10
13.(2024八下·宁江期中)如图,在中,,E为上一动点,M,N分别为的中点,则的长为( )
A.4 B.3 C.2 D.不确定
14.(2024八下·保山期中)如图,在中,,,于点D,E是AB的中点,若DE=2.5,则AB的长为( )
A.2.5 B.5 C.7.5 D.10
15.(2024九下·成都模拟)如图,在矩形中,点在上,且平分,,,则的长为( )
A. B. C. D.
16.(2023九上·包河开学考)如图,在菱形中,,是边上一点,且,有下列结论:
是等边三角形;
;
周长的最小值为;
面积的最大值为.
其中正确结论有( )
A.个 B.个 C.个 D.个
三、解答题
17.(2023七上·天长期中)生活处处有数学,就看你是否有数学的眼光.同学们都见过机械手表吧,让我们一起去探索其中隐含的数学知识
一块手表如图①所示,把它抽象成数学模型:如图②,表带的两端用点A和点表示,表盘与线段交于点、,为表盘圆心.
(1)若为,,是中点,则手表全长______.
(2)表盘上的点对应数字“12”,点对应数字“6”,为时针,为分针,时表盘指针状态如图③所示,分针与重合.
①______度;
②作射线,使,求此时的度数.
18.(2024七下·霍林郭勒期中)在平面直角坐标系中,已知点,若点M到x轴的距离等于5,求m的值.
19.(2023九下·龙江模拟)甲、乙两车分别从相距的M、N两地出发,匀速行驶,先相向而行,乙车在甲车出发后出发,到达M地后停止行驶,甲车到达N地后,立即按原路原速返回M地(甲车调头的时间忽略不计),甲、乙两车距N地的路程y(单位:)与甲车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)甲车的行驶速度是 ,乙车的行驶速度是 , ;
(2)求线段的解析式并写出自变量的取值范围;
(3)乙车出发多少小时后两车相距为?请直接写出答案.
20.(2024八下·北京市期末)定义:对于给定的一次函数. 把形如 的函数称为一次函数的衍生函数.
(1)已知函数, 若点 在这个一次函数的衍生函数图象上,则 ,
(2)已知矩形的顶点坐标分别为,当函数的衍生函数的图象与矩形有1个交点时 .当函数)的衍生函数的图象与矩形有两个交点时,直接写出k的取值范围 .
(3)已知点,以为一条对角线作正方形,当正方形与一次函数的衍生函数图象有两个交点时,求t的取值范围.
四、计算题
21.(2019·怀化模拟)设一次函数y=kx+b(k≠0)的图象经过A(1,3),B(0,-2)两点,试求k,b的值.
22.(2024七下·新华期末)如图,在中,平分,P为线段上的一点,过点P作交的延长线于点E.若,,求的度数.
23.(2024八下·东西湖期末)在菱形中,,点E、F分别为上一点.
(1)如图1,当,时,直接写出三条线段和之间满足的等量关系式为________;
(2)当时,
①如图2,若,若,,求的长;
②如图3,E为中点,交于点G,交于点H,和交于点O,若,,,则________.
答案解析部分
1.【答案】或
【知识点】直角三角形的性质
2.【答案】8
【知识点】平行线之间的距离;正方形的性质
3.【答案】
【知识点】平行四边形的性质
4.【答案】
【知识点】等腰三角形的性质;勾股定理
5.【答案】9
【知识点】解分式方程;频数与频率
6.【答案】(1)
(2)
【知识点】勾股定理的应用
7.【答案】A
【知识点】坐标与图形变化﹣对称
8.【答案】C
【知识点】多边形内角与外角
9.【答案】C
【知识点】菱形的判定;矩形的判定;正方形的判定
10.【答案】C
【知识点】函数自变量的取值范围
11.【答案】B
【知识点】勾股定理的逆定理
12.【答案】C
【知识点】平行四边形的性质;三角形的中位线定理
13.【答案】A
【知识点】平行四边形的性质;三角形的中位线定理
14.【答案】D
【知识点】等边三角形的判定与性质;含30°角的直角三角形;直角三角形斜边上的中线
15.【答案】A
【知识点】勾股定理;矩形的性质
16.【答案】D
【知识点】等边三角形的判定与性质;菱形的性质
17.【答案】(1)
(2)①;②在内部时,,在外部时
【知识点】角的运算;角平分线的性质;线段的和、差、倍、分的简单计算;钟面角
18.【答案】6或1
【知识点】点的坐标
19.【答案】(1),,240;
(2)
(3)或或
【知识点】待定系数法求一次函数解析式;一元一次方程的实际应用-行程问题;通过函数图象获取信息
20.【答案】(1)2 , 3
(2)1,
(3)或 或
【知识点】一次函数的概念;矩形的性质;正方形的性质
21.【答案】解:把A(1,3)、B(0,﹣2)代入y=kx+b得 ,
解得 ,
故k,b的值分别为5,﹣2.
【知识点】待定系数法求一次函数解析式
22.【答案】
【知识点】三角形的角平分线、中线和高;三角形内角和定理;三角形的外角性质;直角三角形的性质
23.【答案】(1)
(2);
【知识点】等边三角形的判定与性质;勾股定理;正方形的性质
21世纪教育网(www.21cnjy.com)
2 / 7
同课章节目录
